La nuova definizione di cristallo – o come vincere un Premio Nobel Understand article
Tradotto da Paolo Sudiro. Perché la simmetria è così importante nella comprensione dei cristalli? E perché una simmetria “proibita” cambia la definizione stessa di cristallo?

concessa da Mark Schellhase;
font dell’immagine: Wikimedia
Commons
Studiare i materiali cristallini è una delle tecniche analitiche più potenti a disposizione degli scienziati. Se è possibile far crescere un singolo cristallo di un sale, di una molecola, proteina o addirittura di un virus, allora è normalmente possibile identificare non solo le sue connessioni (quali atomi sono legati a cosa), ma anche le sue lunghezze di legame, gli angoli di legame e la conformazione molecolare (che forma assume una molecola flessibile). Dallo studio di cristalli proteici è spesso possibile capire come funziona la proteina nel corpo e quali sono i sui siti attivi.
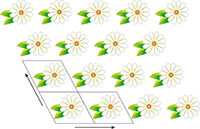
la simmetria traslazionale in
due dimensioni. I
parallelogrammi indicano
l’unità ripetuta. Clicca sull’
immagine per ingrandirla
Immagine gentilmente
concessa da Mairi Haddow
I cristalli sono intrinsecamente belli, grazie soprattutto alla loro simmetria. Convenzionalmente, si riteneva che tutti i cristalli avessero una proprietà in comune: la simmetria traslazionale nelle tre dimensioni. Infatti, è così che sono stati definiti originariamente i cristalli – come materiali nei quali gli atomi, le molecole o gli ioni costituenti sono impacchettati in un arrangiamento tridimensionale ordinato e ripetitivo. La simmetria traslazionale è ben illustrata in due dimensioni pensando ad una carta da parati decorata, che normalmente ha questa proprietà – se stesa appropriatamente. Ciò significa che se noi tracciamo un parallelogramma (tassello) che contiene una certa decorazione, e lo ripetiamo in due direzioni, otteniamo il disegno della carta da parati (figura 1).
In modo analogo, possiamo ottenere una struttura cristallina tridimensionale da una ”scatola” di atomi, ripetendo la scatola lungo gli assi x, y e z. La scatola che si ripete è nota come cella unitaria (figura 2).
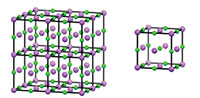
Cliccare sull’immagine per ingrandirla
Immagine gentilmente concessa da Mairi Haddow

struttura atomica dei cristalli
quasi-periodici ad una
riunione del National
Institute of Standards and
Technology, USA, nel 1985 –
pochi mesi dopo avere
pubblicato la sua scoperta
Immagine gentilmente
concessa da Phillip Westcott,
National Institute of Standards
and Technology
Simmetria dei cristalli e quasi-periodicità
I cristalli che possiedono una simile simmetria traslazionale nelle tre dimensioni sono indicati formalmente come cristalli periodici, perché le loro strutture hanno un andamento che si ripete dopo un certa distanza regolare o periodo. Nel 2011, tuttavia, il Premio Nobel per la Chimica venne assegnato a Dan Shechtman per la sua scoperta di cristalli quasi-periodici. Questi cristalli non sono periodici, cioè non possiedono una simmetria traslazionale, ma hanno un ordine locale. Essi hanno la stessa unità ripetuta in vari punti del cristallo, ma non ad intervalli periodici. Il recente riconoscimento di questo lavoro è un trionfo della perseveranza di Shechtman di fronte al ridicolo con cui è stato accolto quando ha pubblicato per la prima volta le sue ricerche (Shechtman et al., 1984). Ma come mai questa idea era così controversa? Perché quei cristalli sembravano avere delle simmetrie proibite dai sistemi periodici.
Oltre alla simmetria traslazionale, molti cristalli periodici hanno ulteriori simmetrie, come la simmetria speculare. Ad esempio, guardando la cella unitaria del cloruro di sodio, possiamo vedere che ciascuna metà della cella è l’immagine speculare dell’altra metà (figura 3; vedi anche figura 4).
Oltre alla simmetria traslazionale, molti cristalli periodici hanno ulteriori simmetrie, come la simmetria speculare. Ad esempio, guardando la cella unitaria del cloruro di sodio, possiamo vedere che ciascuna metà della cella è l’immagine speculare dell’altra metà (figura 4).
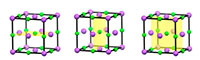
Clicca sull’immagine per ingrandirla
Immagine gentilmente concessa da Mairi Haddow

Clicca sull’immagine per ingrandirla
Immagine di pubblico dominio (simbolo del riciclaggio); le altre immagini sono state gentilmente concesse da Mairi Haddow
Clicca sull’immagine per ingrandirla
Immagine gentilmente concessa da Mairi Haddow
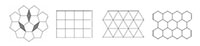
Quando un motivo o un cristallo hanno simmetria traslazionale e periodica, sono anche possibili le simmetrie binaria, ternaria, quaternaria e senaria; ma non si possono avere simmetria quinaria, settenaria, o superiore. Questo perché triangoli, quadrati ed esagoni possono essere disposti in uno spazio bidimensionale senza lasciare alcuno spazio vuoto tra loro. Cosa che diversamente non è possibile usando pentagoni, ettagoni e poligoni con più lati (figura 5).
Come vengono analizzati i cristalli?
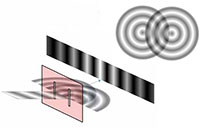
diffrazione di Young, che
dimostra l’interferenza
della luce che passa
attraverso un reticolo di
diffrazione. Clicca sull’
immagine per ingrandirla
Immagine gentilmente
concessa da Mairi Haddow
Molti studenti avranno ripetuto a scuola il famoso esperimento della doppia fenditura di Young, nel quale un laser viene proiettato attraverso due fenditure in un reticolo di diffrazione, separate da una distanza compatibile con la lunghezza d’onda della luce laser. Si vedrà quindi una figura di interferenza, prodotta dall’interferenza distruttiva o costruttiva delle onde diffratte dalle fenditure (figura 6).
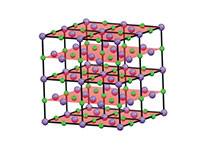
cloruro di sodio che
agiscono nello stesso modo
delle fenditure del reticolo di
diffrazione. Clicca sull’
immagine per ingrandirla
Immagine gentilmente
concessa da Mairi Haddow
I cristalli vengono studiati utilizzando una tecnica nota come diffrazione a raggi X, la cui teoria è stata ampiamente sviluppata nel 1913 da William Henry Bragg e suo figlio William Lawrence Bragg, che nel 1915 vennero entrambi congiuntamente insigniti del Premio Nobel per la loro scoperta. In un esperimento di diffrazione i cristalli agiscono come un complesso reticolo di diffrazione, dove le fenditure sono strati di atomi nel cristallo (figura 7).
Perché si verifichi la diffrazione è necessario che la lunghezza d’onda della luce che interagisce col cristallo sia compatibile con la distanza tra gli atomi.
Normalmente nei laboratori si utilizza la radiazione a raggi X (che vengono diffratti dagli elettroni degli atomi), ma ci sono altre possibilità, come elettroni o neutroniw1.
Il cristallo viene illuminato da un fascio di raggi X di lunghezza d’onda specifica e vengono misurate le figure d’interferenza mentre il cristallo viene fatto ruotare. Per strati di atomi orientati ad un certo angolo q rispetto al fascio di raggi X, i raggi X diffratti saranno in fase (cioè si avrà interferenza costruttiva) se e solo se la differenza tra i percorsi di due raggi X diffratti sarà uguale ad un multiplo intero della lunghezza d’onda, producendo un picco di diffrazione misurabile. Questa è nota come legge di Bragg e in figura 8 viene illustrato come è stata ricavata.
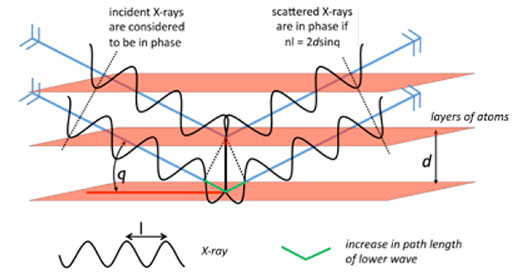
Immagine gentilmente concessa da Mairi Haddow

diffrazione di un cristallo
convenzionale ad un
particolare angolo d’
incidenza. Ogni punto
luminoso (riflessione)
rappresenta l’interferenza
costruttiva di un diverso
livello di atomi. (La forma
sulla destra è l’ombra del
fermaraggio, uno scudo
metallico che assorbe i raggi
X non diffratti)
Immagine gentilmente
concessa da Mairi Haddow
Man mano che il cristallo ruota, diversi strati di atomi soddisferanno la legge di Bragg e produrranno interferenza costruttiva. Il risultato sarà un picco di diffrazione con un’intensità proporzionale al numero e al tipo di atomi dello strato, come illustrato in figura 9. Un tipico esperimento di diffrazione misurerà da migliaia a milioni di riflessioni e per mezzo di un’analisi accurata può essere utilizzato per comprendere l’esatta struttura del cristallo.
Anche la figura di diffrazione prodotta da un cristallo possiede una simmetria, collegata alla simmetria del cristallo. La figura di diffrazione dei cristalli quasi-periodici ha una simmetria proibita nei cristalli periodici, come ad esempio una rotazione quinaria o decenaria.
Le strutture di questi insoliti cristalli sono collegate alle tassellature di Penrose (figura 11). Si tratta di strutture che possiedono una simmetria locale, ma non la simmetria traslazionale.

Immagini gentilmente concesse da Mairi Haddow (immagini a destra e sinistra); immagine al centro gentilmente concessa da Materialscientist; fonte dell’immagine: Wikimedia Commons

può possedere una simmetria
rotazionale quinaria (sopra)
ma questi oggetti non
possono essere combinati in
un sistema periodico. Questo
succede, ad esempio, nella
tassellatura di Penrose
(sotto), nella quale si può
occasionalmente trovare una
simmetria quinaria
localizzata, ma che non ha
simmetria traslazionale.
Clicca sull’ immagine per
ingrandirla
Immagine gentilmente
concessa da Mairi Haddow
Le ricerche in questo campo hanno condotto ad un cambiamento nella definizione di un cristallo da parte dell’Unione Internazionale di Cristallografia nel 1991. I cristalli non hanno più bisogno di possedere una simmetria traslazionale: un materiale è considerato cristallino se mostra una figura di diffrazione definita, che i cristalli quasi-periodici effettivamente producono.
Comunque, è poco probabile che i testi scolastici verranno corretti in tempi brevi per accogliere questa nuova definizione. Fino ad oggi sono stati scoperti molto pochi di questi materiali quasi-periodici ed il primo cristallo quasi-periodico naturale – l’icosaedrite (Al63Cu24Fe13), un materiale di probabile origine meteoritica che è stato trovato nel fiume Khatyrka in Russia orientale, è stato scoperto solo nel 2009 (Bindi L et al., 2009). Sebbene da allora siano stati sintetizzati altri esempi, e sia noto che i quasi-cristalli esistono in molte leghe metalliche ed alcuni polimeri, è molto improbabile che i cristalli che gli studenti producono in laboratorio siano altro che periodici e, tranne che per le loro proprietà insolite ed interessanti, i cristalli quasi-periodici non hanno reali applicazioni – finora.
References
- Bindi L et al. (2009) Natural Quasicrystals. Science 324(5932): 1306-1309. doi: 10.1126/science.1170827
- Shechtman D et al. (1984) Metallic phase with long-range orientational order and no translational symmetry. Physical Review Letters, 53(20): 1951-1953. doi: 10.1103/PhysRevLett.53.1951
Web References
- w1 – L’analisi di diffrazione non è possibile solo con i raggi X, ma anche con neutroni ed elettroni. Lo spiegano tre membri di EIROforum, l’editore di Science in School.
- Lo European Synchrotron Radiation Facility utilizza le figure di interferenza di raggi X ad alta energia per l’analisi dei materiali. Gli esperimenti condotti all’ESRF hanno applicazioni non solo in scienza dei materiali, ma anche in biologia, medicina, fisica, chimica, scienze ambientali e perfino paleontologia e patrimonio storico.
- L’Istituto Laue-Langevin impiega la più potente sorgente stabile di neutroni al mondo. Gli studi di diffrazione per i quali vengono utilizzati i fasci di neutroni riguardano ricerche sulla fisica della materia condensata, chimica, biologia, fisica nucleare e scienza dei materiali.
- Lo European X-ray Free Electron Laser, che si prevede sarà operativo nel 2015, utilizzerà lampi di raggi X per esaminare i campioni. L’idea alla base di un tipico esperimento è semplice: illuminare un campione con intensi lampi di raggi X e contare i fotoni che vengono dispersi dal campione in varie direzioni. Il risultato è una figura di diffrazione.
Resources
- Cornuéjols D (2009) Biological crystals: at the interface between physics, chemistry and biology. Science in School 11: 70-76.
- Per imparare come crescere i vostri cristalli proteici in classe, vedete:
-
Blattmann B, Sticher P (2009) Growing crystals from protein. Science in School 11: 30-36.
-
- Altre informazioni riguardo a Dan Shechtman e la sua scoperta.
- Howes L (2011) Quasicrystals scoop prize. Chemistry World 8(11): 38-41.
- Per un’intervista col matematico e studioso di simmetria Marcus de Sautoy, vedete:
-
Hayes E (2012) La matematica dove meno te l’aspetti: intervista a Marcus du Sautoy. Science in School 23.
-
Review
Come scrive l’autrice, “I cristalli sono intrinsecamente belli”, ma gli studenti spesso considerano la cristallografia un argomento difficile e noioso. Per questi studenti ed i loro insegnanti, l’articolo di Mairi Haddow è un riferimento prezioso per guardare ai cristalli con un approccio nuovo e stimolante. In questo piacevole articolo l’argomento è spiegato in modo chiaro e preciso, insieme con immagini belle ed efficaci (ad esempio quella sulla carta da parati e la simmetria traslazionale).
L’articolo potrebbe essere utilizzato per le lezioni di chimica (strutture solide), fisica (diffrazione, onde, struttura atomica), scienze della Terra (mineralogia, cristallografia), e matematica (simmetria). Questi argomenti, con l’aggiunta di storia dell’arte (tassellatura), offrono varie opportunità interdisciplinari.
Adeguati spunti di verifica includono:
- Dall’articolo potete dedurre che è possibile ottenere dei cristalli da:
- Un sale
- Una molecola
- Un virus
- Un batterio
- Con quali dei seguenti metodi NON si fanno analisi diffrattometriche dei cristalli?
- Raggi X
- Onde radio
- Neutroni
- Laser ad elettroni liberi
- Con quali dei seguenti tasselli è possibile coprire completamente una superficie bidimensionale?
- Triangoli, quadrati, pentagoni ed esagoni
- Triangoli, quadrati, rettangoli ed eptagoni
- Triangoli, quadrati, rettangoli ed esagoni
- Quadrati, rettangoli e pentagoni
Giulia Realdon, Italia





