Den Klimawandel im Klassenzimmer simulieren Teach article
Übersetzt von Thomas Auer. Warum seine Schüler nicht dazu bringen, eigene Prognosen zum Klimawandel abzugeben – mit der Hilfe von Dudley Shallcross und Tim Harrison von der Universität Bristol, Großbritanien?
Klimawandel und globale Erwärmung sind brandaktuelle Themen und verdienen damit in der Schule einen zentralen Platz im naturwissenschaftlichen Stundenplan. Aber wie lässt sich voraussagen, wie sich unser Klima in Zukunft verändern wird? Die Zeit scheint reif, Schüler in die Erstellung einfacher Klimamodelle einzuführen. In diesem Artikel zeigen wir, dass Schüler eine überschaubare Kalkulationstabelle benutzen können, um den Hauptfaktoren, die das Erdklima beeinflussen auf die Schliche zu kommen.
Ein erster Versuch das Klima zu modellieren
Beim einfachsten Klimamodell entspricht die auf die Erde einstrahlende Sonnenenergie der von der Erde abgestrahlten Wärmeenergie; das heißt ein „eintreffende = abgestrahlte Energie“-Modell. Wird in diesem Artikel von „Energie“ gesprochen, so meinen wir eigentlich „Energiefluss“; das heißt Energie pro Sekunde. Von Messungen weiß man, dass die von der Sonne abgestrahlte Energie, die auf die oberste Schicht der Erdatmosphäre (pro Sekunde) einwirkt, und mit der Solarkonstante S bezeichnet wird, 1370 Wm-2 beträgt.
Wir beginnen mit der Berechnung der durchschnittlichen Temperatur, TE, der Erdoberfläche. Nehmen wir an, der Radius einer perfekt sphärischen Erde betrage RE. In unserem einfachen Modell sehen wir, dass die Erde Sonnenstrahlen auf einer Fläche πRE2 absorbiert (was einer flachen Scheibe an Atmosphäre entspricht) aber Energie auf einer Fläche 4πRE2 emittiert (also von der kompletten Oberfläche).
(a) eintreffende = abgestrahlte Energie
sowie unter Berücksichtigung des Stefan-Boltzmann Gesetzes (siehe Box)
(b) Energie pro Flächeneinheit pro Zeiteinheit mal Gesamtfläche(Scheibe) = Energie pro Flächeneinheit pro Zeiteinheit mal Gesamtfläche(Kugel)
(c) 1370 x πRE2 = σTE4 x 4πRE2
Umformen der Gleichung ergibt:
σTE4 = 1370 = S/4
4
TE4 = 1370
(4 x 5,67 x 10-8)
TE = 279 K (6 °C)
wobei s der Stefan-Boltzmann Konstante entspricht (5,67 x 10-8 Wm-2K-4).
Auf den ersten Blick scheint dies eine sinnvolle Zahl für solch ein vereinfachtes Modell zu sein, obwohl die wirkliche Durchschnittstemperatur der Erde bekannterweise 16 °C beträgt. (Es gibt verschiedene Wege dies zu berechnen. Einer davon teilt die Erde in ihre Breitengrade auf, ermittelt die durchschnittliche Temperatur per Breitengrad, summiert diese auf und bildet anschließend den Mittelwert). Das Problem bei dem verwendeten, sehr einfachen Modell liegt jedoch darin, dass ein Teil der Solarenergie nicht von der Erde absorbiert wird. Vielmehr wird ein Teil der Sonnenstrahlen direkt von Wolken und Eis reflektiert und in den Weltraum abgestrahlt.
Etwa 24% der eintreffenden Energie werden von Wolken reflektiert – weitere 6% von der Erdoberfläche z.B. von Eis. Dies ergibt eine Gesamtreflexion der Erde – bekannt als die Albedo (A) – von 30% oder 0,3. Deshalb muss die linke Seite von Gleichung (c) durch den Term 0,7 x 1370 x πRE2 ersetzt werden und die Berechnung von TE ergibt damit:
TE4 = 1370 x 0,7
(4 x 5,67 x 10-8)
TE = 255 K (-18 °C)
Dieser Wert ist offensichtlich bei weitem zu gering und führt zu der Frage: Warum ist die Erde so warm? Um diese Frage beantworten zu können, benötigen wir ein geringfügig komplexeres Modell.
Wichtige physikalische Grundlagen
Die Schwarzkörperstrahlung und das Stefan-Boltzmann Gesetz
Alle Körper emittieren Energie in Form von elektromagnetischer Strahlung. Ein schwarzer Körper absorbiert sämtliche Strahlung, die auf ihn trifft – er emittiert Strahlung als Funktion seiner Oberflächentemperatur.
Das Stefan-Boltzmann Gesetz beschreibt die gesamte Energie, I, die von einem schwarzen Körper bei beliebiger Temperatur, T, ausgestrahlt wird:
I(T) = σT4 (Gleichung 1)
wobei:
I die Energie ist, die pro Flächeneinheit pro Sekund emittiert wird (Wm-2)
T bezeichnet die absolute Temperatur (K)
σ steht für die Stefan-Boltzmann Konstante (5,67 x 10-8 Wm-2K-4).
Das „einschichtige Erdatmosphäre“-Modell
Falls wir annehmen, dass die Atmosphäre aus nur einer einzigen Schicht vermischbarer Gase besteht, so können wir ein genaueres Modell entwerfen, welches für Schüler mit Hilfe einer Kalkulationstabelle anwendbar ist. Bei diesem Modell wird berücksichtigt, dass die Atmosphäre sowohl Teile des eintreffenden, sichtbaren Sonnenlichts als auch des von der Erde abgestrahlten infra-roten Lichts absorbiert.
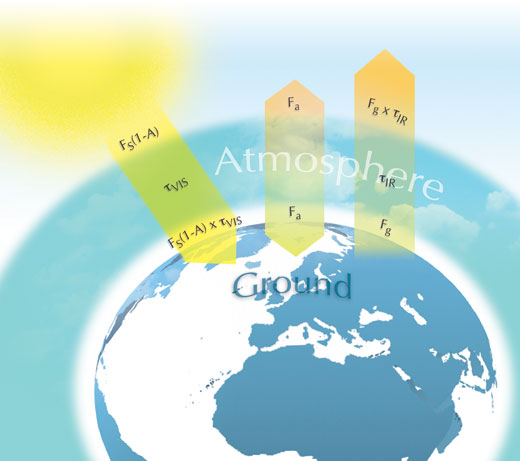
Die unten stehende Abbildung fast die Elemente des Modells zusammen. FS bezeichnet die Solarkonstante geteilt durch 4 (S/4), und ergibt sich aus der Differenz zwischen eintreffender Energie verteilt auf eine Scheibe, πr2, und abgestrahlter Energie von der Oberfläche einer Kugel, 4πr2 der Vorraussetzung, die schon im ersten Model galt). Die von der Sonne eintreffende Energie beträgt dann FS(1-A), wobei A die Albedo bezeichnet – denjenigen Anteil, der zurück in den Weltraum reflektiert wird. Die eintreffende Energie erstreckt sich über das UV und sichtbare Spektrum. τVIS ist der Anteil der eintreffenden Energie, der nicht von der Atmosphäre absorbiert wird. Absorbiert die Atmosphäre 100%, so ergibt sich für τVIS der Wert 0; absorbiert die Atmosphäre nichts, so beträgt der Wert von τVIS 1. Damit erreicht die Oberfläche der Erde Energie im Wert von FS(1-A) x τVIS.
Die Erde wird sich ähnlich einem schwarzen Körper verhalten und die mit Fg bezeichnete Energie von ihrer Oberfläche emittieren. Diese terrestrische Strahlung konzentriert sich dabei auf den infra-rotem Bereich des Spektrums. Bestimmte Gase in der Atmosphäre absorbieren infrarote Energie (Treibhausgase). Ähnlich τVIS, so bezeichnet τIR den Anteil der Energie im infraroten Bereich, der nicht von Treibhausgasen absorbiert wird. Die abgestrahlte Energie beträgt somit Fg x τIR.
Unter der Annahme, dass die Energie, die auf der Erdoberfläche auftrifft und von dieser abgestrahlt wird mit der Energie im äußeren Bereich der Atmosphäre im Gleichgewicht steht, und die Energie der Atmosphäre als Fa bezeichnet wird, so gilt:
an der Erdoberfläche:
FS(1-A) x τVIS + Fa = Fg (Gleichung 2)
und an der Obergrenze der Atmosphäre:
Fg x τIR + Fa = FS(1-A) (Gleichung 3)
Gleichung 2 und 3 zusammengefasst ergibt:
Fg = FS(1-A)(1 + τVIS)
(1 + τIR)
Letztendlich:
Fg = σTE4 = FS(1-A)(1 + τVIS)
(1 + τIR)
TE = [ FS(1-A)(1 + τVIS) ]0,25
[ σ(1 + τIR) ] (Gleichung 4)
Setzen wir dann folgende Werte ein:
FS = 1370/4 = 342,5 Wm-2 (Solarkonstante geteilt durch 4)
A = 0,3
τVIS = 0,8
τIR = 0,1
So gibt uns Gleichung 4:
TE = 288,5 K (15,5 °C),
was einer sehr guten Annäherung an die tatsächliche Durchschnittstemperatur der Erdoberfläche entspricht.
Gleichung 4 kann man nun in einem Programm wie Microsoft Excel einsetzten, so dass die Schüler sehen können, wie sich die globale Temperatur bei Veränderung der Gleichungsparameter verändert. Dies wurde bereits gemacht und eine interaktive Version kann online verwendet oder von der Homepage der Universität Bristolw1 heruntergeladen werden.
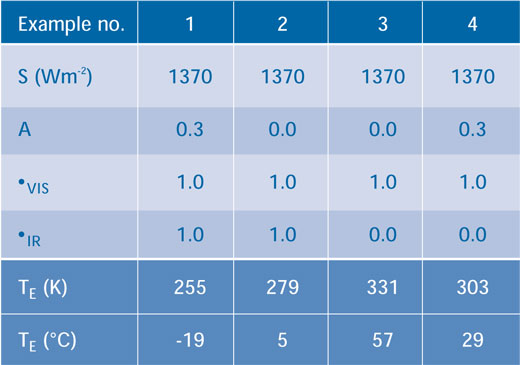
Tabelle 1 zeigt einige Ergebnisse mit veränderten Variablen A, τVIS und τIR. Im Beispiel 1 nehmen wir an, dass die Atmosphäre weder eintreffende noch reflektierte Strahlung aufnimmt (das heißt sowohl τVIS und τIR entsprechen dem Wert 1.0) und die Albedo 0,3 bei einer Temperatur von 225 K beträgt. In Beispiel 2 gehen wir von keinerlei Wolken oder Eis auf der Erde aus (das heißt A = 0,0) was die Erdtemperatur auf 279 K erhöht und die Wichtigkeit der Albedo zeigt. Beispiel 3 geht wieder von A= 0,0 aus, aber diesmal absorbiert die Atmosphäre die gesamte abgestrahlte Energie im infraroten Bereich (das heißt τIR = 0.0). Die Erde erwärmt sich auf 331 K. Wenn wir nun in Beispiel 4 Wolken und Eis wieder mit berücksichtigen (A = 0,3) fällt die Temperatur auf 303 K.
Mögliche Fragen
Typische Fragen, die gestellt werden können und bei deren Beantwortung die Schüler auf die Verwendung des Modells angewiesen sind:
- Welche der Variablen hat den größten Effekt auf die durchschnittliche Erdtemperatur?
- Würde man die durchschnittliche Entfernung Erde – Sonne um 1 % der jetzigen Distanz erhöhen, so würde dies die Solarkonstante um den Faktur 1,0201 erniedrigen, das heißt sie würde 1343 Wm-2 betragen. Wie hoch wäre die Temperatur? Nimm eine Albedo von 0,3, τIR von 0,3 und τVIS von 0,6 an!
(Die Solarkonstante ist proportional zur Entfernung im Quadrat; ein Platzieren der Erde um 10% näher an der Sonne würde damit bedeuten S = 1370/(0,9)2 = 1691 Wm-2 , das Entfernen der Sonne um 1% S = 1370/(1,01)2 = 1343 Wm-2).
Natürlich können auch um einiges anspruchsvollere Fragen gestellt werden:
- Würde der Sand der Sahara zu Glasspiegeln verarbeitet werden (Sand kann zu Glas geschmolzen werden),
- Wie groß müsste der Spiegel sein, um den Planeten um 1 °C abzukühlen?
- Welchem Anteil der Sahara würde dies entsprechen?
Ein komplexeres Modell
Wie kann man unser einfaches Modell mit einem komplexeren Modell, wie dem Hadley Centre Klimamodell, das vom nationale meteorologische Dienst des Vereinigten Königreichs (siehe Bilder unten) verwendet wird, vergleichen? De facto sind sich beide Modelle sehr ähnlich, nur dass das Hadley Centre Klimamodell die Atmosphäre nicht als einheitliche Schicht betrachtet sondern in eine Vielzahl von Abschnitte, basierend auf Längen-, Breitengraden und Höhe über dem Meeresspiegel, unterteilt. Für jeden Abschnitt berechnet das Modell direkt die Summe an eintreffender UV/sichtbarer Strahlung die den Abschnitt durchquert oder aber von ihm gestreut wird. Weiterhin wird die Summe an austretender Infrarotstrahlung, die den Abschnitt durchquert, unter Berücksichtigung der Konzentration der wichtigsten Treibhausgase und der Oberfläche von Wolken und Eis gemessen. Die ausgeklügeltste Version des Hadley Centre Modells bezieht außerdem den Wärmefluss in und aus den Ozeanen sowie die CO2 Aufnahme der Vegetation mit ein. Sollten Sie also die Prinzipien des einfachen Klimamodells verstehen, so sind Sie auf dem besten Weg, auch das komplexere, reale Klimamodell zu begreifen.
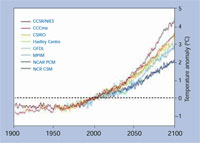
Erwärmung; Voraussage des
Klimamodels zur globalen
Erwärmung relativ zur globalen
Durchschnittstemperatur im Jahr
2000. Die verwendeten Daten
stammen vom Intergovernmental
Panel on Climate Change Data
Distribution Centre. Zum
Vergrößern Bild anklicken.
Mit freundlicher Genehmigung von
Robert A. Rohde; Bildquelle:
Wikimedia Commons.
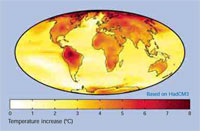
Erwärmung; 2070-2100 Voraussage
im Vergleich zum Durchschnitt
1960-1990. Eine Karte der geschätzten
globalen Erwärmung zum Ende des
21ten Jahrhunderts. Das Modell zeigt
einen Temperaturanstieg um 3,0 °C und
beruht auf dem Hadley Centre HadCM3
Klimamodell. Zum Vergrößern Bild anklicken.
Mit freundlicher Genehmigung von Robert A.
Rohde; Bildquelle: Wikimedia Commons.
An einer echten Klimasimulation teilnehmen
Climateprediction.netw2 ist das größte laufende Experiment, welches versucht eine Vorhersage des Klimas des 21ten Jahrhunderts zu treffen. Es tut dies unter Einbindung von Privatpersonen auf der ganzen Welt, die Zeit auf ihrem Computer zur Verfügung stellen – immer dann wenn der Computer eingeschalten ist, aber nicht dessen volle Kapazität ausgeschöpft wird. Das komplette Klimamodell besitzt eine Vielzahl an veränderbaren Parametern; um all diese Parameter zu bestimmen muss eine phänomenal große Zahl an Simulationen durchlaufen werden. Allein mit der Rechenleistung, die dem climateprediction.net Team zur Verfügung steht, würde solch ein Ensemble an Simulationen eine sehr lange Zeit in Anspruch nehmen. Die Idee hinter climateprediction.net ist, dass jedermann eine Version des Modells herunterladen kann, welches dann einen bestimmten Parameter berechnet (voreingestellt). Die Laufzeit des Modells beträgt dabei etwa drei Monate und es läuft im Hintergrund während Sie arbeiten, ohne die Geschwindigkeit des Rechners zu beeinträchtigen.
Berechnungen werden in drei Teilen durchgeführt:
Der erste Teil führt Kalkulationen unter Berücksichtigung von Klimadaten der Jahre 1850 bis 1900 durch und vergleicht die resultierenden Vorhersagen mit realen Temperaturaufzeichnungen: Dies wird als Eichung bezeichnet. Im zweiten Teil wird eine Simulation des Klimas von 1901 bis heute durchlaufen. Der dritte Teil dann simuliert das zukünftige Klima (2000-2100) unter Veränderung eines einzigen Parameters. Zum Beispiel die Empfindlichkeit des Klimas auf Schwankungen im Schwefelkreislauf. Sobald die Kalkulation beendet ist, werden die Daten automatisch beim nächsten Zugriff aufs Internet an den nationalen meteorologischen Dienst des Vereinigten Königreichs übertragen. Die Simulationssoftware (gebührenfrei) liefert dem Computernutzer eine grafische Darstellung der Klimaveränderung, so wie sie berechnet wurden. Temperaturveränderungen je Jahreszeit mit entsprechendem Längen-, Breitengrad und Höhe über dem Meeresspiegel sind nur einige der Variablen, die bildlich dargestellt werden können. Solch ein Hilfsmittel würde ein fächerübergreifendes Schulprojekt ermöglichen und eine Brücke von Geografie hin zu physikalischen Fächern schlagen.
In der nächsten Ausgabe von Science in School, stellen die Autoren einige chemische Experimente, die mit dem Klimawandel zu tun haben vor.
Web References
- w1 – Eine interaktive Version des einfachen Klimamodells kann online verwendet oder hier heruntergeladen werden: www.chemlabs.bris.ac.uk/outreach/resources/simple_climate_model/index.html
- Benutzen Sie die Schieberegler um die Variablen zu verändern.
- w2 – Für weitere Details über das Experiment und wie man sich selbst einbringen kann, besuchen Sie: http://climateprediction.net.
- Die climateprediction.net Seite bietet darüber hinaus Informationen und Materialien speziell für Schulen, verfügbar in Englisch und Spanisch: http://climateprediction.net/content/resources-schools
Resources
- Harrison T, Shallcross D, Henshaw S (2006) Detecting CO2 – the hunt for greenhouse-gas emissions. Chemistry Review 15: 27-30
- Pacala S, Socolow R (2004) Stabilisation wedges: solving the climate problem for the next 50 years with current technologies. Science 305: 968-972. doi: 10.1126/science.1100103
- Shallcross D (2006) Dirty Air. Education in Chemistry, 43 (5): 131-135
- Zahlreiche, von den Autoren zur Verfügung gestellte Informationen für Lehrer zum Thema Luftverschmutzung, Klimawandel und Ozonloch: www.chemlabs.bristol.ac.uk/outreach/resources/Atmos.html
- Eine hervorragende Quelle für Grafiken und klimarelevante Daten findet sich unter: www.grida.no/climate/vital/index.htm
- Daten von der Earth System Research Laboratory Global Monitoring Station sind einzusehen unter: www.cmdl.noaa.gov
- Die Adresse der Homepage des Zwischenstaatlichen Ausschuss über Klimaveränderungen, wo der Bericht zum Klimawandel 2007 und andere Daten zu finden sind, lautet: www.ipcc.ch
- Haubold B (2008) An Inconvenient Truth. Science in School 9: 72. www.scienceinschool.org/2008/issue9/inconvenient
Review
Klimawandel sollte mit Sicherheit eines der Themen der naturwissenschaftlichen Ausbildung für alle Schularten europaweit sein. Insbesondere nach Al Gore’s medienwirksamer Inconvenient Truth Kampagne hat das Thema weltweite Aufmerksamkeit auf sich gezogen. Nichtsdestotrotz ist es oft schwierig, nützliches Lehrmaterial mit ausreichenden Hintergrundinformationen für Lehrer naturwissenschaftlicher Fächer zu finden. Dieser zweiteilige Artikel nun bietet eine brauchbare und leicht anzuwendende Einstiegsmöglichkeit in den eher komplizierten Prozess der Klimamodellierung.
Während das mathematische Modell wohl am Besten für den Gebrauch in Fortgeschrittenenklassen für Schüler ab 16 Jahren und älter geeignet ist, so können die grundlegenden Phänomene ohne Probleme auch jüngeren Schülern vermittelt werden – selbst wenn sie sich im späteren Verlauf ihres Schullebens nicht auf Naturwissenschaften spezialisieren wollen. Die angeführten Internetquellen bieten eine Vielzahl an unterschiedlichen Ansätzen, gebrauchsfertigen Bildern, kleinen Anwendungen und Grafiken und stellen damit eine nützliche Quelle für jeden Lehrer dar.
Tobias Kirschbaum, Deutschland





