How much carbon is locked in that tree? Teach article

Author(s): Andreas Schwarz, Wibke Niels, Tobias Fuchs, Kirsten Schlüter, Tamaryin Godinho and Michael Meyer

Biology, maths, and the SDGs: estimate the CO2 absorbed by a tree in the schoolyard and compare it to the CO2 emissions of a short-haul flight.

Global warming and the associated climate change are the greatest challenges facing humankind over the next ten years. A reduction in the levels of the greenhouse gas carbon dioxide (CO2) plays a key role in mitigating climate change. As trees absorb CO2 to generate their own biomass, they are part of a global strategy to reduce CO2 levels. But how many trees are needed to offset one flight, for example?

This project starts with the following question: how many trees from the schoolyard are needed to remove the CO2 released when someone takes a plane trip? The worked example in this article is based on 680 kg of CO2, which is one person’s CO2 emissions for a round-trip holiday from Germany to Mallorca by air, but teachers can also pick a destination of equivalent distance from their city or look up the emissions for a more locally relevant route.

In the following materials, students estimate the carbon-storage capacity of a tree in the schoolyard or nearby and compare that to the CO2 emissions of an aeroplane trip, as well as using a Geogebra sheet to better understand intercept theorem. In addition to mathematical content, students recognize the importance of trees in mitigating anthropogenic CO2 emissions through CO2 uptake through photosynthesis and reflect on CO2 emissions in everyday life. This multidisciplinary project ties together curriculum topics from multiple subjects, from maths (geometry and ratios) to biology (photosynthesis) and chemistry (organic compounds and molecular masses). It also ties in with the 17 UN sustainable development goals (SDGs), of which the preservation and protection of the environment on land and water, as well as access to quality education, are key objectives.

The activities are suitable for students aged 11–16, with younger students working through the steps and the teacher explaining everything, and more independent problem-solving and in-depth discussion for older students.

How much carbon do trees store?

Trees need CO2 for their growth, but too much CO2 is responsible for global warming. To slow down the resulting climate change and to limit global warming to 1.5°C, according to the Paris Climate Agreement of 1995, CO2 emissions have to be reduced to net zero by 2050 and greenhouse gases have to be removed from the atmosphere by 2100.[1–3]

Students should know that trees absorb CO2 and understand the role of CO2 as a greenhouse gas in the atmosphere. However, it is often wrongly assumed that CO2 is stored. Trees only use carbon (C) to generate biomass by photosynthesis. If one wants to describe the climate effect of trees correctly, one must speak of carbon binding and not of CO2 binding.

A forest in southern Germany
Image courtesy of Tamaryin Godinho

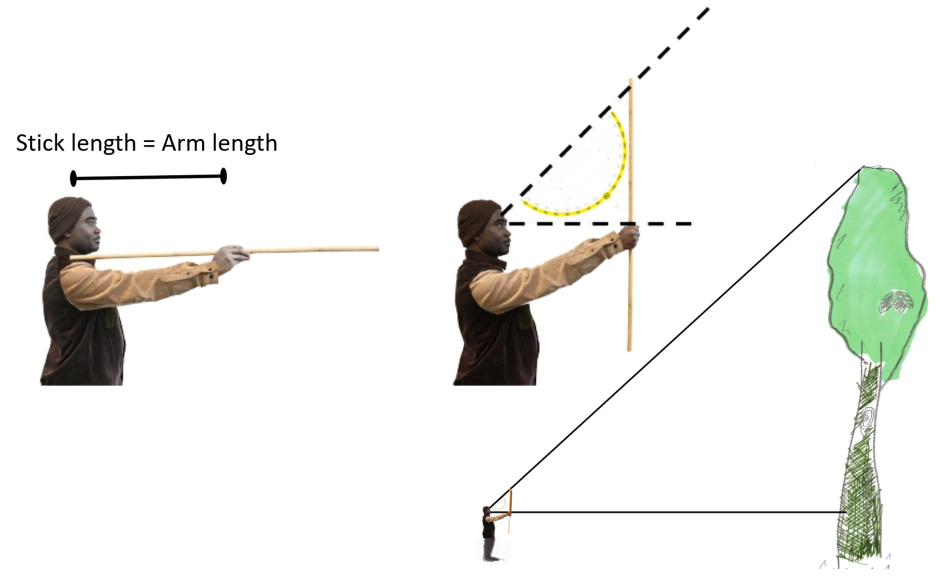
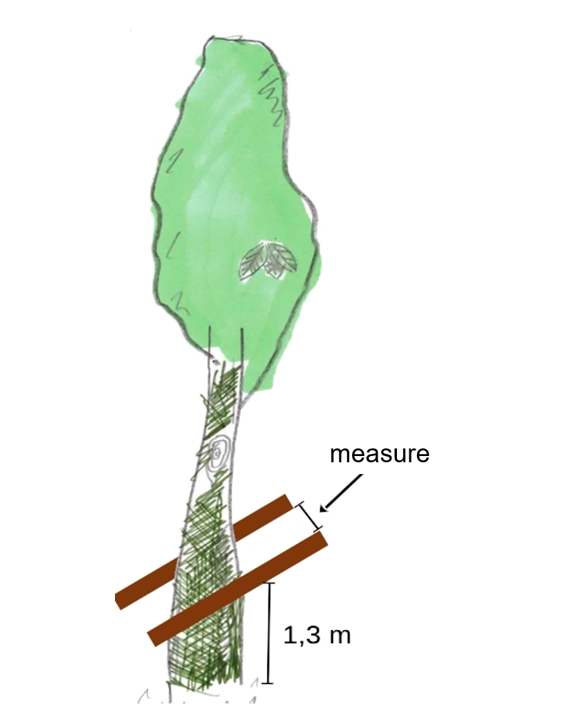
To estimate the amount of CO2 taken up by a tree, one has to estimate the volume of the tree based on its height and diameter at breast height (DBH), defined as 1.3 m, which is the internationally standardized height at which to determine a tree’s diameter.[4,5] A common method for estimating the height of a tree is based on the so-called forester triangle (the walking-stick method), which is based on the intercept theorem. Subsequently, the weight of the calculated volume is determined with the help of the specific weight of the wood of the respective tree species. Notably, this does not include the roots and the amount of biomass, such as sugars given to fungus via the roots into soil, and in general, the roots contribute approximately 30% of the total biomass of a tree.[5–7] Moreover, the sugars from photosynthesis are also used for growth, respiration, and conversion into amino acids and lipids. Therefore, calculations in this activity reflect a rough estimation.

Given that approximately 50% of the dry weight of wood is carbon (although this is a simplification: C content varies among species[8]), one has to divide the calculated weight by two to obtain the amount of C in kg. Finally, to calculate the mass of CO2 absorbed, the C content of the tree must be multiplied by 3.67 (see molecular mass of CO2).

Considering, that every tree species has its own shape and weight, there are different estimation tables available. For simplicity, this activity does not differentiate between different tree species, but is limited to deciduous broadleaf and coniferous trees.

Activity 1: Introduction to the problem

Before proceeding with the practical part of the lesson, a class discussion introduces students to the main question and encourages them to think about the different aspects of the answer.
This activity should take around 30 mins.

Materials

  • Tree carbon estimation tables, which give approximate estimates of the amounts of atmospheric carbon conifers and broadleaf trees of different sizes have incorporated into their above-ground biomass
  • Optional: atlas and a pair of compasses or access to an online map tool with a radius calculator (e.g., this radius-around-a-point tool)

Procedure

  1. Introduce the main question: one person causes 680 kg of CO2 release during a round trip of 2686 km (1343 km each way) by air, which is the distance from Düsseldorf (Germany) to Mallorca and back.
    How many trees are needed to remove this 680 kg of CO2 from the air?
  2. Optional: encourage students to use the atlas and pair of compasses, or online maps with a radius calculator tool, to find a travel destination that is approximately 1343 km from their nearest airport.
  3. Ask what information you’d need to estimate the amount of CO2 fixed by a tree in its life so far. The first question is where does the CO2 absorbed by plants go? You can mention photosynthesis as a hint.
  4. Optional: depending on the ages of the students, you might discuss some of the compounds trees build from the products of photosynthesis, like cellulose and lignin, and look up their chemical structures and identify the positions where carbon is.
  5. Having established that much of the carbon from CO2 fixation ends up in the wood, the next question is how much wood mass does a particular tree contain? What parameters does this depend on? Students should be able to figure out that this depends on the volume, which will be influenced by the size, for example, height and girth, of the tree. Older students might also consider wood density.
  6. Introduce the tree carbon estimation tables, and explain that they can be used to estimate that amount (mass) of wood in a tree with a particular height and diameter at breast height (DBH). Mention that this measures the above-ground mass only, and neglects other ways trees might add biomass to the soil, so it underestimates the total carbon fixation.

Activity 2: Measuring the height and diameter of a tree in the schoolyard

In this activity, students select a tree, measure its DBH, and use a forester’s triangle to measure the height. The forester’s triangle is first employed before teaching intercept theorem to show the practical relevance of this method.

This activity takes around 30 mins.

The forester’s triangle

  • The forester takes a stick and places one end of the stick on their shoulder with their arm outstretched. The stick is then exactly as long as their arm (hand-to-shoulder distance = hand-to-eye distance when using the triangle)
  • Subsequently, they align the stick vertically so that an imaginary line between their eye and hand forms a right angle (figure 1)
    IMPORTANT: the forester holds their hand at eye level!
  • The forester moves away from the tree until they can see the top of the tree above the tip of the stick.
  • The height of the tree corresponds approximately to the distance between the forester and the tree plus the height of the forester’s eye.
Figure 1: Application of the forester’s triangle method
Image courtesy of Dr Andreas Schwarz

Materials

  • Worksheet 1
  • Tape measure or folding ruler and some string and a marker
  • Tape, sticky notes, or other means to mark the tree without damaging it.
  • Some sticks that are slightly longer than the students’ arms
  • A fairly large tree with enough space around it that the crown can be seen and you can walk the same distance away as the tree’s height; this might be in the schoolyard, a local street, or a park
  • Objects to mark position (e.g. wooden blocks, stationary, rocks)
  • Pencil and paper to record results

Procedure

Part 1 – Diameter at breast height (DBH)
  1. Divide the students into groups of three. Small groups allow each student to be involved in measuring.
  2. Students should measure the point on the trunk 1.3 m above the ground using the folding ruler or tape measure and mark this without damaging the tree (e.g., with a piece of tape).
  3. They should then use the tape measure to measure the trunk circumference in cm at this point. Alternatively, they can wrap a piece of string around the tree and mark the points where the string ends touch, and then measure the length of the string between the marked points. Note this value on worksheet 1.
  4. They can then use the following formula to calculate the diameter from the circumference:

d = C/π

where d=diameter and C=circumference.

  • Alternatively, younger students who aren’t familiar with circle formulae can hold two sticks parallel on either side of the tree and measure the distance between them to get the diameter (figure 2).
Figure 2: Measurement of the trunk DBH (1.3 m)
Image courtesy of Dr Andreas Schwarz
Part 2 – Height
  1. Still in their groups, students should read the forester’s triangle instructions on worksheet 1.
  2. One student should follow the instructions, holding the stick as described, and then walk backwards/forwards until the top of the stick lines up with the top of the tree. Another student should put a hand on their shoulder and make sure they do not walk into anything while walking backwards or focussing on the top of the stick.
  3. The position on the ground should then be marked with an object.
  4. The students should then measure the distance in m from the object to the tree trunk using the folding ruler or tape measure.
  5. Ideally, each student should take a turn to make their own measurement and record the value in the worksheet. The height of the tree corresponds approximately to the distance between the forester and the tree.
  6. Optional: ask students to look at the figure again. A distance is missing to determine the exact height of the tree. Which distance is it? Hopefully, some of them should see that the eye height of the forester should be added.
  7. Optional: students can compare their values (as long as they are working on the same tree) and discuss the variation and possible sources of error.

Discussion

For younger students, it may be sufficient to know how the forester’s triangle works, and to discuss the kind of triangles shown on the diagram and their basic properties (a right-angled isosceles triangle). But with older students, it may be valuable to explore the mathematical theory (intercept theorem) behind the forester’s triangle by employing a mathematical simulation. For this, you can use the Intersect Theorem activity in the supporting material.

Activity 3 – Final calculation: how many trees?

Finally, the students can use their measurements (height and DBH) to determine the amount of CO2 the tree has absorbed in its lifetime by employing estimation tables.

Broadleaf trees, such as beech and oak, generally grow more slowly than conifers (such as spruce or fir) and have denser and more complex vascular bundles, which makes them harder and heavier. This is why conifers are often referred to as softwoods and broadleaf trees are often referred to as hardwoods, although there is considerable variation between species. For this reason, separate estimation tables for conifer and broadleaf trees are given.

We offer two approaches.
1) Using worksheet 2, students first estimate the amount of carbon atoms fixed in the trunk and branches of the tree, and from that, they can then calculate the amount of absorbed CO2.
2) In a simpler alternative, students use worksheet 3 to obtain the amount of CO2 directly from the estimation table without further calculations.

Subsequently, the students can calculate how many trees of similar type/size/age would be needed to absorb the CO2 produced by a flight of 2 × 1.343 km by dividing 680 (CO2 released by the flight) by the amount of CO2 having been absorbed by the measured tree.

This activity takes 20 minutes.

Materials

Procedure

  1. Students need to identify whether the tree they measured is a conifer or broadleaf tree. Explain these terms to students if necessary.
  2. Using the tree height and DBH measured in Activity 2, they should read off the carbon mass from the carbon estimation table and fill in the value on worksheet 2.
    Simpler option: for younger or less able students, they can read the CO2 mass directly from the CO2 estimation table instead and enter it on worksheet 3, and then proceed straight to step 5.
  3. Remind students that this is the mass of carbon, and ask what would be needed to get the equivalent mass of CO2 absorbed? Hint: compare the atomic mass of carbon with the molecular mass of CO2. They should be able to calculate that the carbon mass should be multiplied by 3.67.
  4. Students should then calculate the amount of CO2 the tree had absorbed to build its aerial parts during its life (carbon mass from the table × 3.67).
  5. Finally, they can calculate how many trees of similar type/size/age would be needed to absorb the CO2 produced by a flight of 2 × 1343 km by dividing 680 (CO2 released by the flight) by the CO2 amount calculated in Step 4, or read from the CO2 mass estimation table.

Discussion

The results can be used as a basis for discussion or further research/class projects on a number of themes. Possible questions include the following:

  • This calculation only includes the above-ground parts of a tree. How much of a tree’s biomass is underground?
  • How old is the tree/how long would it have taken to absorb that much CO2? How would you find out? Is there a way to estimate this without harming the tree?
  • What happens to this carbon when the tree dies? What about if the tree is used for heating? Or for paper/cardboard packaging?
  • Do all trees absorb similar amounts of CO2, or does it depend on where they grow and on the surrounding conditions? When trees are planted to address deforestation, is it important what trees are used?
  • What other environmental benefits do trees provide? Is there a difference between mature mixed forests and monoculture plantations?
  • What other ecosystems absorb CO2? How much CO2 do these different ecosystems currently absorb?
  • Which has the greatest environmental impact: protecting existing forests or planting more trees? What are the threats to the world’s forests?
  • What alternatives are there to flying? Do they release more or less CO2 for the same journey distance? Which forms of transport are the most environmentally friendly?
  • What aspects of our everyday life contribute to our carbon footprint? Which steps can we take personally to reduce our carbon footprint? What changes can reduce the carbon footprint of a school?

Overall, it is important that students understand how vital forests are for the planet and why we need to protect them, but they shouldn’t come away with the simplistic idea that we can keep releasing CO2 at the current rate and global warming can be solved by simply planting trees.

Acknowledgements

We thank Mr. Minka Aduse-Poku for his support.

We thank the Bayerische Landesanstalt für Wald und Forstwirtschaft for providing the estimation tables.[9]

We are very grateful to the FNR Waldklimafonds (supported by the German Federal Ministry of Food and Agriculture and the German Federal Ministry for the Environment, Nature Conservation, Nuclear Safety and Consumer Protection) for funding our project, WaldKlimaLehrpfade (funding code: 2218WK27X5), in which the teaching sequence presented here was developed. Further teaching materials (in German) can be found on the website https://waldklima.uni-koeln.de.

References

[1] Friedlingstein P et al. (2021) Global carbon budget. Earth System Science Data 14: 1917–2005. doi: 10.5194/essd-14-1917-2022

[2] United Nations Environment Programme’s Paris Agreement: https://unfccc.int/sites/default/files/english_paris_agreement.pdf

[3] Smith S et al. (2023) The State of Carbon Dioxide Removal 1st edition. OSF. doi: 10.17605/OSF.IO/W3B4Z

[4] Burns RM, Honkala BH (1990) Silvics of North America: Volume 2, Hardwoods. U.S. Department of Agriculture, Forest Service, Washington, DC. ISBN: 0160292603

[5] Brokaw N, Thompson J (2000) The H for DBH. Forest Ecology and Management 129: 89–91. doi: 10.1016/S0378-1127(99)00141-3

[6] Sinacore K et al. (2017) Unearthing the hidden world of roots: root biomass and architecture differ among species within the same guild. PLoS ONE 12: 1–22. doi: 10.1371/journal.pone.0185934

[7] Harrison MJ (2005) Signaling in the arbuscular mycorrhizal symbiosis. Annual Review of Microbiology 59: 19–42. doi: 10.1146/annurev.micro.58.030603.123749

[8] Lamlom SH, Savidge RA (2003) A reassessment of carbon content in wood: variation within and between 41 North American species. Biomass Bioenergy 25: 381–388. doi: 10.1016/S0961-9534(03)00033-3

[9] Klein D, Schulz C (2011). Kohlenstoffspeicherung von Bäumen. LWF-Merkblatt 27.

Resources

Cutting-edge science: related EIROforum research

Institut Laue-Langevin (ILL)

Are there other ways of capturing CO2 from the atmosphere? Researchers are investigating a variety of possibilities at ILL! For example, salty water can act as a carbon sink, trapping CO2 in deep saline aquifers with high pressures and temperatures. Scientists are in the process of studying what happens to this CO2. Another exciting approach is to capture and re-use CO2 by converting it into chemicals that are useful to make pharmaceutical drugs and other high-value products.

Author(s)

Dr Andreas Schwarz (biologist), Wibke Nils (geographer), Tobias Fuchs (teacher), and Prof. Kirsten Schlüter (director) are from the Institute of Biology Education, and Prof Michael Meyer is director of the Institute of Mathematics Education at the University of Cologne, Germany. All focus on current didactic efforts for interdisciplinary teaching of sustainable development, environmental protection, inquiry-based learning, and health for children and adults.

Dr Tamaryin Godinho is the executive editor of Science in School. She is passionate about science and believes that evidence-informed decision-making is crucial for addressing today’s challenges and building a better future.

Review

This cross-curricular activity encourages teachers to make the most of trees on their school grounds. A set of three hands-on tasks, enable pupils to explore the intercept theorem at the same time as supporting the delivery of a wide range of topics, from photosynthesis and the carbon cycle to climate change and sustainability. By estimating tree height, pupils can get to grips with geometry and ratios, whilst considering the bigger picture in terms of carbon offsetting and the value of forested landscapes.

Samantha Dobbie, Birmingham Institute of Forest Research (BIFoR), UK

License

CC-BY
Text released under the Creative Commons CC-BY license. Images and supporting materials: please see individual descriptions.

Related articles

Understand

When plants moved ashore and changed the planet

Plants today are extremely diverse, abundant, and flamboyant. However, the first land plants, which initiated a great change in the flora and fauna on planet Earth, were very different.

Biology, Chemistry, Earth science

   

Teach

Graphing stories

Sketch graphs from ‘story’ videos of everyday events to help students understand the basic features of graphs and how to interpret…

General science, Mathematics, Physics

   

Teach

Do you know your water footprint?

Fresh water is a scarce resource on our planet – but how many of us are aware of how much water is needed to make the foods we eat every…

Biology, Chemistry, Earth science, Health, Science and society