A nova definição de cristais – ou como ganhar um Prémio Nobel Understand article
Traduzido por Ana Luísa Carvalho. Porque razão é a simetria tão fundamental para a compreensão da natureza dos cristais? E porque razão a simetria "proibida" alterou a definição do que é um cristal?

Schellhase; Fonte da Imagem:
Wikimedia Commons
O estudo de materiais cristalinos é uma das mais poderosas técnicas analíticas disponíveis para os cientistas. Se é possível crescer um cristal único de um sal, molécula, proteína ou mesmo de um vírus completo, então, é normalmente possível identificar não só a sua conectividade (que átomos estão ligados ao quê), mas também os seus comprimentos e ângulos de ligação e a sua conformação molecular (a forma adoptada por uma molécula flexível). A partir do estudo de cristais de proteína é possível elucidar como funciona essa proteína num organismo e onde se encontram os seus sítios activos.
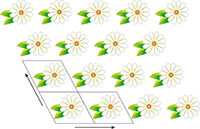
ilustrando a simetria
translacional em duas
dimensões. Os
paralelogramos indicam a
unidade que se repete.
Clique na imagem para
ampliar
Imagem cortesia de Mairi
Haddow
Os cristais possuem uma beleza inerente, graças, em grande parte, à sua simetria. Por convenção, todos os cristais possuem uma propriedade em comum: simetria translacional em três dimensões. De facto, foi assim que os cristais foram originalmente descritos – como materiais onde os átomos, moléculas ou iões constituintes se encontram empacotados num padrão tridimensional repetitivo e com uma ordem regular. A simetria translacional é melhor ilustrada em duas dimensões imaginando papel de parede estampado, que geralmente possui esta propriedade – se pendurado correctamente. Isto significa que podemos desenhar um paralelogramo (mosaico ou azulejo) contendo um determinado padrão e, dispondo esse mosaico em duas direções, obtemos o padrão estilo papel de parede (figura 1).
De forma semelhante, podemos obter a estrutura cristalina 3D de uma “caixa” de átomos, por repetição da caixa ao longo dos eixos x, y, e z. A caixa que se repete é designada por célula unitária (figura 2).
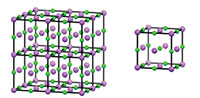
Imagem cortesia de Mairi Haddow

estrutura atómica de cristais
quasi-periódicos num
encontro científico no
National Institute of
Standards and Technology
(Instituto Nacional de
Padrões e Tecnologia), EUA,
em 1985 – alguns meses
depois de publicar a sua
descoberta
Imagem cortesia de Phillip
Westcott, National Institute of
Standards and Technology
Simetria em cristais e quasi-periodicidade
Os cristais que possuem simetria translacional em três dimensões são formalmente designados de cristais periódicos, porque as estruturas possuem um padrão que se repete a uma determinada distância ou período. No entanto, em 2011, o Prémio Nobel da Química foi atribuído a Dan Shechtman pela sua descoberta dos cristais quasi-periódicos. Estes cristais não são periódicos – não possuem simetria translacional – mas, ainda assim, possuem ordem local. Possuem a mesma unidade repetitiva em diferentes pontos do cristal, mas não a intervalos periódicos. O reconhecimento recente deste trabalho é um triunfo para a perseverança de Shechtman, ultrapassando a ridicularização que recebeu quando primeiramente publicou o seu trabalho (Shechtman et al., 1984). Mas, então, porque era esta ideia tão controversa? Porque, aparentemente, estes cristais possuem simetrias que são proibidas em sistemas periódicos.
Além da simetria translacional, a maior parte das estruturas cristalinas periódicas possui simetria adicional, tal como simetria de espelho. Por exemplo, observando a célula unitária do cloreto de sódio, podemos ver que cada metade corresponde à imagem no espelho da outra metade (figura 3; ver também figura 4).
A simetria rotacional é igualmente possível. Isto significa que se pegarmos num objecto e o rodarmos em torno de um ponto central por um determinado número de graus, a sua imagem permanecerá inalterada (figura 4).
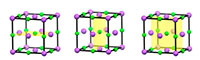
Clique na imagem para ampliar
Imagem cortesia de Mairi Haddow

Clique na imagem para ampliar
Imagem de domínio público (símbolo de reciclagem); outras imagens cortesia de Mairi Haddow
Clique na imagem para ampliar
Imagem cortesia de Mairi Haddow
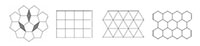
Quando um padrão ou cristal possuem simetria translacional e esta é periódica, as simetrias rotacionais de grau 2, de grau 3, de grau 4 e de grau 6 são todas possíveis. No entanto, o mesmo não acontece com as simetrias de grau 5, ou 7 ou superior. Isto acontece porque é possível, no espaço 2D, empacotar triângulos, rectângulos, quadrados ou hexágonos sem deixar espaços vazios entre eles. O mesmo não é possível usando pentágonos, heptágonos ou polígonos superiores (figura 5).
Como são analisados os cristais?
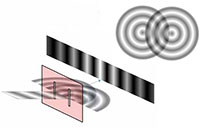
difração de Young,
mostrando a interferência da
luz que passou através da
grelha de difração. Pressione
o botão do rato sobre a
imagem para aumentar
Imagem cortesia de Mairi
Haddow
Já muitos estudantes terão realizado a famosa experiência de Young, na qual se faz passar um feixe de laser através de duas fendas numa grelha de difração, sendo o espaço entre as fendas comparável ao comprimento de onda do laser. Pode observar-se um padrão de interferência, resultante das interferências construtivas e destrutivas entre as ondas difratadas pelas fendas (figura 6).
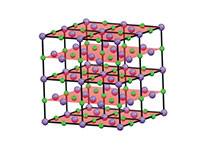
de cloreto de sódio que
actuam de forma semelhante
às fendas de uma grelha de
difração. Clique na imagem
para ampliar
Imagem cortesia de Mairi
Haddow
Os cristais são estudados usando uma técnica conhecida por difração de raios-X, cuja teoria foi extensamente desenvolvida em 1913 por William Henry Bragg e pelo seu filho William Lawrence Bragg, que, pelo seu trabalho, partilharam o Prémio Nobel da Física em 1915. Numa experiência de difração, os cristais comportam-se como uma complexa grelha de difração, onde as “fendas” correspondem a camadas de átomos no cristal (figura 7).
Para que ocorra difração, o comprimento de onda da radiação que interage com o cristal tem que ser comparável à distância entre os átomos.
Frequentemente, em laboratórios, a radiação usada é a radiação X (cujos raios são dispersos pelos eletrões nos átomos), mas existem outras possibilidades, como eletrões ou neutrõesw1.
O cristal é montado no percurso de um feixe de raios-X com um comprimento de onda selecionado, e o padrão de difração é registado à medida que o cristal é rodado em torno de um eixo. Para as camadas de átomos posicionadas a um ângulo θ do feixe de raios-X, os raios dispersos encontrar-se-ão em fase (i.e. possuem interferência construtiva) se, e só se, a diferença de percurso entre dois raios dispersos for igual a um número inteiro de comprimentos de onda, resultando num pico de difração mensurável. Isto é conhecido como a Lei de Bragg e a sua dedução é ilustrada na figura 8.
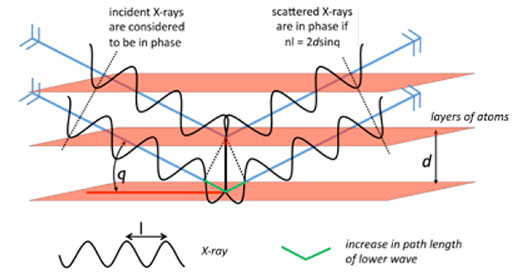
Imagem cortesia de Mairi Haddow

difração de um cristal
convencional medido a um
determinado ângulo. Cada
mancha brilhante (reflexão)
representa a interferência
construtiva de uma camada
diferente de átomos. (A
forma à direita é a sombra do
“beam stop”, um escudo
metálico que absorve o feixe
dos raios-X não difratados)
Imagem cortesia de Mairi
Haddow
À medida que o cristal é rodado, diferentes camadas de átomos irão satisfazer a Lei de Bragg e produzir interferência construtiva. Isto resulta num pico de difração com uma intensidade relacionada com o número e tipo de átomos da camada, como é, por exemplo, mostrado na figura 9. Uma experiência de difração típica irá medir de milhares a milhões de reflexões, e uma análise cuidada permitirá obter a estrutura exata do cristal.
O padrão de difração produzido por um cristal também possui simetria e esta está relacionada com a simetria do cristal. Os padrões de difração de cristais quasi-periódicos possuem simetria que é proibida em cristais periódicos, tal como a rotação de grau 5 ou de grau 10 (figura 10).
As estruturas destes cristais invulgares estão relacionadas com os mosaicos tipo Penrose (figura 11). Estes são estruturas que possuem simetria local, mas não possuem simetria translacional.

Imagens cortesia de Mairi Haddow (imagens esquerda e direita); Imagem central cortesia de Materialscientist; Fonte da Imagem: Wikimedia Commons

pode possuir simetria
rotacional de grau 5 (em
cima) mas estes objetos não
podem ser integrados num
sistema periódico. Isto
ocorre, por exemplo, em
mosaicos Penrose (em baixo),
onde é possível encontrar
simetria local de grau 5, mas
que não possuem simetria
translacional. Clique na
imagem para ampliar
Imagem cortesia de Mairi
Haddow
A investigação nesta área levou a uma alteração na definição de um cristal pela União Internacional de Cristalografia em 1991. Os cristais já não têm necessariamente que conter simetria translacional: um material é um cristal se apresentar um padrão de difração bem definido, o que é uma certeza em cristais quasi-periódicos.
No entanto, é pouco provável que os programas escolares venham a ser alterados em breve para incluírem esta nova definição. São poucos os materiais quasi-periódicos já descobertos, e o primeiro cristal quasi-periódico natural – icosaedrite (Al63Cu24Fe13), um material provavelmente originário de um meteorito e descoberto no rio Khatyrka no leste da Rússia – foi apenas identificado em 2009 (Bindi L et al., 2009). Embora mais exemplos tenham sido criados posteriormente, estando os quasi-cristais presentes em muitas ligas metálicas e alguns polímeros, os cristais que os estudantes crescem em laboratório pouco provavelmente são alguma coisa que não seja periódica e, apesar das suas características invulgares e interessantes, os quasi-cristais não possuem qualquer aplicação prática – ainda.
References
- Bindi L et al. (2009) Natural Quasicrystals. Science 324(5932): 1306-1309. doi: 10.1126/science.1170827
- Shechtman D et al. (1984) Metallic phase with long-range orientational order and no translational symmetry. Physical Review Letters, 53(20): 1951-1953. doi: 10.1103/PhysRevLett.53.1951
Web References
- w1 – A análise por difração é possível não só com raios-X, mas também usando neutrões e electrões. Isto é exemplificado por três membros do EIROforum, entidade responsável pela publicação da Science in School.
-
O European Synchrotron Radiation Facility a instituição europeia de radiação de sincrotrão, usa os padrões de difração de raios-X de elevada energia para a análise de materiais. As experiências realizadas no ESRF têm aplicação não só em ciência dos materiais, mas também em biologia, medicina, física, química, ciência ambiental e até paleontologia e património cultural.
-
O Institut Laue-Langevin opera a mais intensa fonte estável de neutrões do mundo. Os estudos de difração com feixes de neutrões são usados na investigação em física da matéria condensada, química, biologia, física nuclear e ciência de materiais.
-
O European X-ray Free Electron Laser ou laser de raios-X de electrões livres), com início de operação programado para 2015, usará flashes de raios-X para examinar amostras. A ideia básica por trás de uma experiência típica é simples: iluminar uma amostra com ondas intensas de raios-X e contar os fotões que são dispersos pela amostra em diferentes direções. O resultado é um padrão de difração.
-
Resources
- Cornuéjols D (2009) Biological crystals: at the interface between physics, chemistry and biology. Science in School 11: 70-76.
- Para aprender como crescer cristais de proteína na escola, consultar:
-
Blattmann B, Sticher P (2009) Growing crystals from protein. Science in School 11: 30-36.
-
- Mais informação sobre Dan Shechtman e a sua descoberta.
- Howes L (2011) Quasicrystals scoop prize. Chemistry World 8(11): 38-41.
- Para uma entrevista com o matemático e investigador em simetria Marcus de Sautoy, consultar:
-
Hayes E (2012) Finding maths where you least expect it: interview with Marcus du Sautoy. Science in School 23: 6-11.
-
Review
Tal como escreve a autora, “os cristais possuem uma beleza inerente”, mas os alunos frequentemente encaram a cristalografia como um assunto difícil e entediante. Para estes estudantes e para os seus professores, o artigo da Mairi Haddow é um material de apoio precioso para uma abordagem nova e inspiradora aos cristais. Neste artigo de leitura agradável, o tópico é explicado numa linguagem clara e precisa, associado a imagens belas e impressionantes (por exemplo, a que se refere ao papel de parede e à simetria translacional).
O artigo pode ser usado no âmbito dos planos curriculares de química (estruturas de sólidos), física (difração, ondas, estrutura atómica), ciências da terra (mineralogia, cristalografia) e matemática (simetria). Estes temas, associados a história da arte (azulejaria), oferecem diferentes oportunidades interdisciplinares.
Como questões para avaliação da compreensão incluem-se:
- A partir do artigo pode deduzir que é possível crescer um cristal de:
- Um sal
- Uma molécula
- Um vírus
- Uma bactéria
- Com quais dos seguintes NÃO é possível realizar uma análise por difração?
- Raios-X
- Pndas de rádio
- Neutrões
- Laser de electrões livres
- Com quais dos seguintes tipos de mosaicos é possível cobrir completamente uma superfície 2D?
- Triângulos, quadrados, pentágonos e hexágonos
- Triângulos, rectângulos e heptágonos
- Triângulos, quadrados, rectângulos e hexágonos
- Quadrados, rectângulos e pentágonos
Giulia Realdon, Itália





