Agudeza visual: ¿con qué nitidez podemos ver realmente? Teach article

Traducido por Pilar Bustos-Sanmamed. El estudio detallado de la agudeza visual requiere no solo de ensayos biológicos sino también de algunos conocimientos de física básica.

La agudeza visual es la medida del nivel de precisión de nuestra visión, particularmente de la capacidad con la que podemos determinar los pequeños detalles. Los ópticos evalúan esto haciéndonos leer en un cartel hasta que las letras se vuelven demasiado pequeñas para que las descifremos con claridad.

Uno de los factores biológicos que determina la agudeza visual es la densidad de células fotoreceptoras de la retina (ver el recuadro “Cómo funcionan nuestros ojos”). Esto nos hace plantear una pregunta intrigante: ¿aumentar la densidad de receptores en la retina haría nuestra visión más nítida? Para responder a esta pregunta, necesitamos tener en consideración tanto la biología del sistema de la visión como la física de la luz. Estos temas están integrados en la mayoría de los planes de estudio para las asignaturas de Biología y Física de la secundaria. Sin embargo, tradicionalmente se abordan por separado, frecuentemente a diferentes grupos de estudiantes. Contrario a esto, el plan de estudios cruzado propone capacitar a los estudiantes para que adquieran una comprensión profunda tanto de la biología como de la física relativa a la agudeza visual y transmitir un importante mensaje general: muchos problemas de la Ciencia Moderna pueden resolverse mejor mediante colaboraciones y un equipo de trabajo interdisciplinares.

En este artículo se describe una forma sencilla de evaluar la agudeza visual creando un cartel y usándolo para calcular la resolución del ojo. Este método puede usarse para estimar la distancia mínima a la que la imagen de dos puntos proyectados sobre la retina pueden identificarse como dos objetos diferentes. Un experimento adicional, disponible en el material extra, relaciona esta distancia con los límites teóricos de la agudeza visual basado en las propiedades físicas de la luz.

Las dos actividades están orientadas a estudiantes de 16-19 años, para realizarlas en un tiempo aproximado de dos horas cada una, incluido la preparación y el análisis de datos. Deberían emplearse otras dos horas más para la discusión de resultados.

Cómo funcionan nuestros ojos 

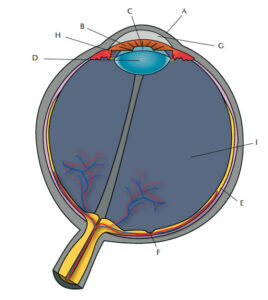
Los rayos luminosos reflejados por los objetos entran en los ojos a través de la pupila. Cuatro de los componentes de los ojos – la cornea, el cristalino, el humor acuoso y el humor vítreo – concentran los rayos de luz en la retina, la parte posterior del globo ocular (figura 1). La retina está organizada en diferentes capas, una de ellas está formada por millones de fotorreceptores sensibles a la luz que transmiten la señal al cerebro a través de otras células como las células ganglionares. Las células fotorreceptoras son células nerviosas especializadas y se dividen en dos tipos – bastones y conos (nombrados así por su forma). Los conos, localizados principalmente en el centro de la retina, permiten la visión con detalle en colores bajo condiciones de alta luminosidad. Los bastones, localizados hacia los bordes de la retina, nos ayudan a detectar el movimiento y a ver en condiciones de baja luminosidad y, nos permiten tener vision periférica. La densidad de fotorreceptores en la retina (que puede ser de unas 200.000 células por milímetro cuadrado en la fovea central) juegan un papel importante en la agudeza visual.

Calculando la resolución del ojo humano

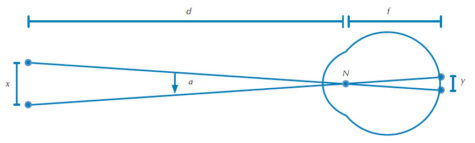
La resolución angular del ojo humano es una medida del ángulo más pequeño entre dos puntos que son percibidos como diferentes y está relacionada en parte con la densidad de fotorreceptores de la retina. Equivale a un minuto de arco (1/60 parte de un grado). En esta actividad, la resolución angular se calcula determinando la relación de la distancia entre los dos puntos y la distancia entre el observador y los puntos. Este método matemático simplificado (que reemplaza cálculos más complicados de la tangente del ángulo α en la figura 2) es posible porque la resolución angular adquiere valores muy pequeños. En matemáticas, este atajo es conocido como la aproximación de ángulos pequeños. El valor calculado puede ser usado para estimar la distancia entre dos puntos proyectados en la retina, como se muestra en la figura 2.

Los estudiantes crearán un cartel con líneas negras simples separadas por espacios de anchura variable. Se les pedirá que indiquen qué líneas perciben como separadas y cuales parecen fusionadas y, usarán estos resultados para hacer un cálculo estimado de la resolución angular y de esta forma el espacio entre los receptores en los ojos.

Materiales

• Ordenador con un programa sencillo de dibujo instalado
• Impresora y papel blanco
• Cinta métrica
• Regla milimetrada

Método

1. Pide a tus estudiantes que usen el programa de dibujo y creen un cartel de barras negras separadas por espacios pequeños. La anchura de estos espacios deben variar entre 0,5 mm y 5 mm y, las barras deben de estar en una sola página, igual que en la figura 3. Poner una o dos barras enteras sin sepración como control.
2. Pide a tus estudiantes que hagan un cartel adicional usando el mismo patrón de barras en filas individuales como en el paso 1 pero ordenadas de forma aleatoria.
3. Imprime los carteles en un papel blanco usando la opción de calidad alta.
4. Pon el cartel en la pared de una sala bien iluminada y pon en el suelo un punto de mira a unos 7-10 m aproximadamente de distancia del cartel. Mide exactamente esta distancia (d)
5. Agrupa a los alumnos en parejas o en grupos pequeños, así se les podrá pedir que lean un cartel diferente del que diseñaron. Uno de los miembros del grupo es el sujeto, que esperará fuera de la habitación, mientras el otro, el experimentador, seleccionará el cartel.
6. Pide al sujeto que entre en la habitación y que se sitúe en el punto de observación mientras el experimentador tapa el cartel elegido.
7. Repetir hasta que todos los estudiantes hayan sido tanto sujetos como experimentadores.
8. Usando la regla, determinar el ancho x del espacio más pequeño del cartel que cada estudiante fue capaz de distinguir correctamente.
9. Para cada estudiante, usa los valores de la distancia desde el cartel, d, y el espacio más pequeño percibido, x, para calcular la resolución angular α (en minutos de arco), que viene dada por la ecuación 1. Asegúrate de que las unidades para d y x son las mismas.
   α = (180x / dπ)60                          Ecuación 1
10. ¿Cuál es el rango de valores de α para los distintos estudiantes? ¿Cuál es la media de la resolución angular para ese grupo de estudiantes? Estima el error para las medidas teniendo en cuenta la precisión cuando mides d con la cinta métrica y x con la regla.
11. Ahora calcula la distancia y entre la imagen de dos puntos cuando se proyecta en la retina. Para este cálculo, se asume un modelo simplificado del sistema óptico del ojo con una sola superficie refractaria y un índice de refracción uniforme. La distancia focal f de este ojo reducido es 20,1 mm. La distancia entre dos puntos de la retina viene dado por los términos de la ecuación 1 para la ecuación 2:
    y = (απf) / (180 ⋅ 60)                      Ecuación 2
12. Pregunta a tus estudiantes cuál, teóricamente, sería el número mínimo de fotorreceptores necesarios para diferenciar con nitidez esos dos puntos. ¿Cuál sería la distancia de centro a centro de estos fotorreceptores?

¿Qué está sucediendo?

La resolución angular del ojo humano oscila normalmente en torno a 40 segundos de arco y 1 minuto de arco. Para percibir dos puntos separados, al menos se necesitan tres fotorreceptores dispuestos en fila: uno para recibir luz desde cada uno de los puntos y, uno para para el hueco entre los puntos. Para la resolución angular de 1 minuto de arco (que corresponde a 0,3 m en una distancia de 1 km), las imagenes de la retina están separadas por, aproximadamente, 6 µm, lo que significa que la distancia de centro a centro de dos receptores vecinos es de 3 µm. Para una resolución angular de 40 segundos de arco, la distancia entre los puntos de la imagen es aproximádamente 4 µm.

La verdadera resolución del ojo depende no sólo de la separación entre fotorreceptores, sino también de la difracción de la luz a su paso por la pupila. Puedes profundizar más sobre esto descargándote el experimento 2.

Entonces, ¿puede mejorarse la agudeza visual si se incrementa la densidad de conos en la retina?

Una resolución angular de 40 segundos de arco a 1 minuto de arco se consigue solo cuando miramos fíjamente un objeto. La imagen del objeto se proyecta en una parte concreta del centro de la retina, la fovea, que contiene solamente fotorreceptores de tipo cono. La densidad de conos en la fovea es más elevada que en cualquier otro lugar de la retina y, los conos aquí tienen un diámetro de solo 3 µm (comparado con los 10 µm de otras zonas de la retina). Dejando lugar para el espacio extracellular alrededor de cada cono (ej. para el transporte de nutrientes), la distancia de centro a centro entre conos en la fovea es de unos 4 µm. Por lo tanto, la densidad de conos en la fóvea está casi próxima a la máxima capacidad posible.

Como puede analizarse en el siguiente experimento, la difracción de la luz en el ojo significa que la distancia mínima que puede diferenciarse entre dos puntos de luz es de unos 5 µm, dada una distancia mínima establecida entre conos de aproximadamente 2,5 µm. Dejando lugar para cierto espacio extracellular entre conos, esta distancia teórica establecida concuerda con los 4 µm de distancia real entre los receptores de tipo cono en la fovea. Además un mayor incremento en la densidad de los conos no sería biológicamente posible y, considerando las limitaciones físicas determinadas por las propiedades de la luz, no ocasionarían ninguna ganancia significativa de la agudeza visual.