La dinámica de la enfermedad: entendiendo la propagación de las enfermedades Teach article

Traducido por Pilar Bustos-Sanmamed. Enfrentarse con la expansión de las enfermedades infecciosas con estas actividades para clase, resaltando las aplicaciones en la vida real de las matemáticas de la escuela.

Las escuelas son el caldo de cultivo para las infecciones: los estudiantes están en constante interacción entre ellos y, a menudo no tienen aún desarrollada la inmunidad las enfermedades. Entendiendo que estas interacciones son vitales para predecir como una enfermedad infecciosa – como es la gripe – se expande. Para los escolares, es importante reflexionar sobre sus interacciones sociales y comprender los tipos de análisis que pueden usarse para determinar la dinámica de la enfermedad

Estas actividades transversales son para estudiantes de 12-15 años, aunque algunas son adecuadas para alumnus más jóvenes o más mayores también.TLas actividades pueden realizarse por equipos de distinto tamaño, desde pequeños grupos hasta toda la clase. Los recursos no requieren nada más que las diapositivas que pueden descargarse desde la sección de materiales addicionales^w1, papel y dados.

Actividad 1: Duración de la enfermedad

Esta actividad corta y para toda la clase simula el comienzo de una enfermedad, el síntoma por el que se pone en marcha. El objetivo es ver cómo de rápido la enfermedad se expande de forma exponencial a través de la clase. Con cada paso, el número de estudiantes que están infectados se duplica (ver figura 1). Esto ayudará a los estudiantes a entender que no se necesitan muchos pasos entre un brote y la propagación a través de una población susceptible.

Los estudiantes descubrirán que la velocidad a la que la enfermedad se propaga depende del número de individuos que son susceptibles o están infectados. No obstante, esto es solamente un modelo matemático simple para determinar la propagación de una enfermedad, ya que asume que todo el mundo es susceptible de ser infectado y que exactamente dos individuos son infectados por cada persona.

Método

1. Comenzar con toda la clase sentada. Pedir un voluntario para ser el primer caso.
2. El primer voluntario debe entonces levantarse e “infectar” a dos compañeros señalándolos.
3. Estos dos estudiantes, a continuación, también se levantarán al haber sido infectados.
4. Cada uno de estos dos estudiantes infectarán a su vez a otros dos estudiantes más de la clase y, así se continuará, hasta que toda la clase esté de pie.
5. Preguntar a los estudiantes cuántos pasos ha llevado infectar a la clase.

Discusión

• Pregunta a tus estudiantes que estimen el número de pasos que se necesitarían para infectar a su escuela, ciudad,  país o el mundo. Se necesitan aproximadamente 33 pasos para infectar el mundo con una población de 8,5 miles de millones (ya que se dan 2ⁿ nuevos casos en la generación n del brote de la enfermedad).
• ¿Qué ocurriría si cada persona infectara 3 ó 4 personas en vez de a 2?
• ¿Qué puede decirnos esto sobre cómo se propagan las enfermedades infecciosas?
• ¿Cuáles son las limitaciones de esta simulación de un brote?

R₀ y redes

R₀ (de otra forma conocido como índice de transmisibilidad) es una medida usada en epidemiología para indicar el promedio de gente que una persona infecta durante el transcurso del periodo contagioso (asumiendo que nadie en la población es inmune a la enfermedad). Si R₀ es mayor de uno, la enfermedad se expandirá a través de la población. Si R₀ es menor de uno, los casos de enfermedad disminuirán y la propagación no tendrá lugar.

R₀ varía dependiendo del tiempo durante el que el paciente es contagioso, el número de personas susceptibles dentro de la población y, el método de transmisión. Las enfermedades que se transmiten por el aire, como el sarampión, generalmente tienen un R₀ más alto que aquellas que se transmiten a través de los fluidos corporales, como el Ébola.

Para los epidemiólogos es importante saber no solo el número de gente que cualquier persona pueda infectar (R₀), sino también como el brote puede extenderse a través de la población. Así, es vital entender la dinámica de la comunidad o de la población. Esto se hace observando cómo los individuos interaccionan unos con otros y, la frecuencia con que lo hacen. De esta forma, los matemáticos pueden elaborar modelos introduciendo esta información en sus simulaciones para comprender como un brote se puede extender a través de la población. Esto resulta vital para los investigadores en ciencias de la salud, puesto que les ayuda a rastrear individuos que pueden haber sido infectados. También puede indicar qué patrones de comportamiento social necesitarían ser modificados si un brote da comienzo, como el distanciamiento social o la cuarentena.

Si bien el Ébola tiene igual de bajo el R0 que la gripe, se convirtió rápidamente en un brote importante en el este de África con una alta tasa de mortalidad – algo que generalmente limitaría la propagación de una enfermedad ya que las personas mueren demasiado pronto como para infectar a un gran grupo. Entonces, ¿cuál fue la mayor causa de la propagación?

La epidemia se desencadenó, en parte, por azar; la primera persona que se infectó resulto ser un tradicional curandero en Sierra Leona, cuyo funeral atrajo a una gran multitud (Freiberger, 2015). La tradición cultural de bañar al difunto para el entierro produjo un aumento de la transmisión y, las personas que tocaron el cuerpo infectado llevaron la enfermedad con ellos según viajaban a otros lugares. El brote además tuvo lugar en un área con un pobre sistema sanitario que fue incapaz de llevar a cabo el control de la infección.

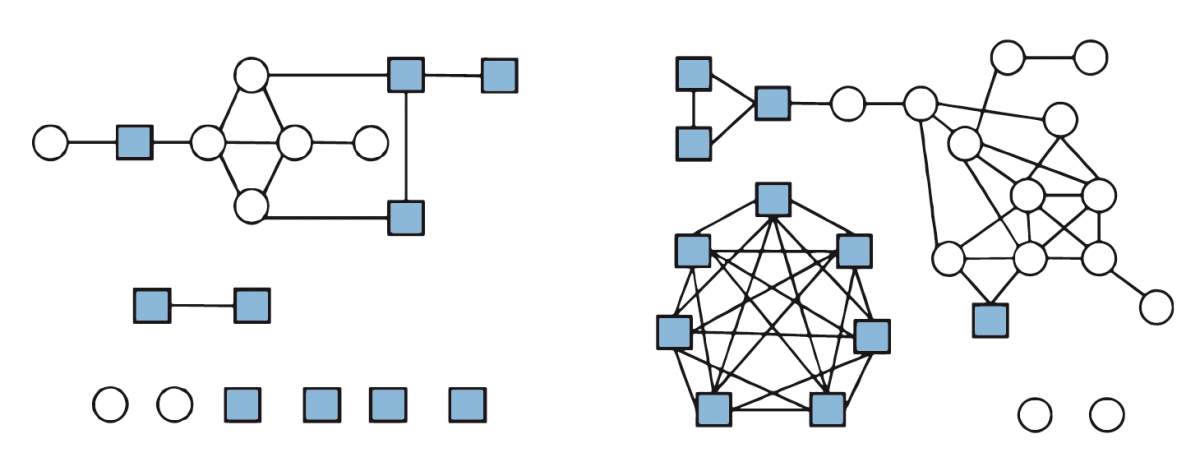
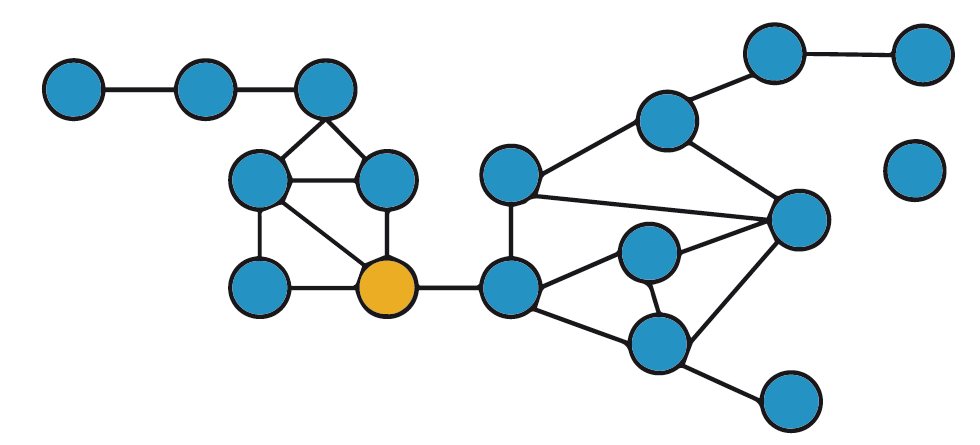
Este ejemplo demuestra que el R0 de un patógeno puede variar en los diferentes brotes. La expansión de la gripe, por ejemplo, será probablemente diferente en un grupo de entre 4 y 5 años de edad y un grupo de entre 10 y 11 años. La figura 2 muestra las interacciones entre individuos en estos dos grupos de edad en un día de escuela en particular. En el grupo con menos edad, hay menos interacciones entre los individuos en comparación con el grupo de mayor edad, en el cual es evidente la existencia de dos grandes pandillas en función del sexo. Los nodos individuales sin interacción alguna indican que un estudiante estuvo ausente en ese día.

Actividad 2: clasificación R₀

Método

1. En grupos pequeños, pide a tus estudiantes que elaboren una lista de cinco enfermedades infecciosas (rabia, gripe, Ébola, varicela y sarampión) según el orden que ellos creen que tienen de mayor a menor índice de transmisibilidad. A continuación revela cada R₀ (0, 1-2, 1-2, 10, 16-18, respectivamente), ¿era lo que los estudiantes esperaban?

Discusión

• ¿Hay alguna relación entre la gravedad de los síntomas y el R₀?
• ¿Qué podéis decir sobre las enfermedades con alto R₀ (ej. sarampión y varicela) – por qué son tan altos?
• ¿Por qué el R₀ de la rabia es 0? No se conoce transmisión de humano a humano.
• ¿Por qué el Ébola es tan preocupante cuando su valor R₀ es bajo?
• ¿Por qué el R₀ de un mismo patógeno puede variar en diferentes brotes?

Actividad 3: Comparando redes

Método

1. Muestra a la clase los diagrámas^w1 de dos redes sociales diferentes: una con 4 a 5 años de edad y, una con 10 a 11 años (ver figura 2). Pregunta a los alumnos qué diferencia creen que hay.
2. Discute por qué estos patrones en las redes se diferencian a lo largo del tiempo.

Discusión

• ¿Cómo/por qué la red social cambia entre los 4-5 años de edad y los 10 a 11 años?
• ¿Esperaríais que esta red cambie de nuevo a la edad de 16 años? ¿Y para adultos?

Actividad 4: Propagación de la enfermedad a través de una red

Método

1. Separar la clase en parejas o en pequeños grupos. Reparte a cada grupo fotocopias de una red social^w1 (figura 3) y un dado.
2. Todo el mundo es inicialmente susceptible; escoge un punto de la red en la fotocopia para ser la primera persona infectada.
3. Por turnos, recorre todos los contactos de la persona  infectada. Para cada uno, tira el dado; si saca un 1 ó un 2, esa persona también se infecta. Si sacan cualquier otro número, son inmunes.
4. Repite para cada nuevo caso de infección  – y así, hasta que se haya tirado el dado para cada uno de los contactos de la persona infectada.
5. Cuenta cuántos casos de infección hay en el grupo y, cuantos pasos se han dado en total para infectarlos.
6. Repite el ejercicio varias veces, con diferentes puntos de partida. Anota el número de casos para cada vez.
7. Estos datos pueden usarse para realizar más análisis, ej. La media, mediana, moda y distribución. Pide a los alumnos hacer la gráfica de puntos (ej. Figura 4) y analiza sus resultados entre pequeños grupos – o en la clase entera.

Discusión

• ¿Por qué se infectan sólo los nodos cuando se saca 1 ó2?
• ¿Qué ocurriría si dejásemos que 1, 2, 3 ó 4 infectaran a alguien?
• ¿Qué ocurre si se comienza en diferentes lugares de la red?
• ¿Por qué el brote cambia de tamaño con cada simulación?

Actividad de ampliación: vacunación selectiva

Los estudiantes pueden reflexionar sobre estas cuestiones de forma individual y después exponerlas a la clase entera:

• ¿A quién vacunarías dentro de la red?
• Si sólo tuvieras 2 ó 3 dosis de vacunas para la red, ¿a quién elegirías para vacunar y por qué?
• ¿Protegerías a la gente con mayor número de uniones o, te centrarías en romper la red en determinados lugares?

Agradecimientos

Las actividades de aprendizaje de este artículo están adaptadas a partir de la colección Dinámicas de la enfermedad NRICH^w2. Actividades adicionales están disponibles en esta colección con el objetivo de mostrar cómo las matemáticas pueden usarse para entender las epidemias, las interacciones sociales y la vacunación.