Supporting materials
Adapting the activity to different age groups
Download
Download this article as a PDF

This activity was presented at the Science on Stage Festival 2022 ![]()
Everybody dance now: students hold ropes and dance to form a topological tangle. Using fraction arithmetic, the knot will finally be untied!
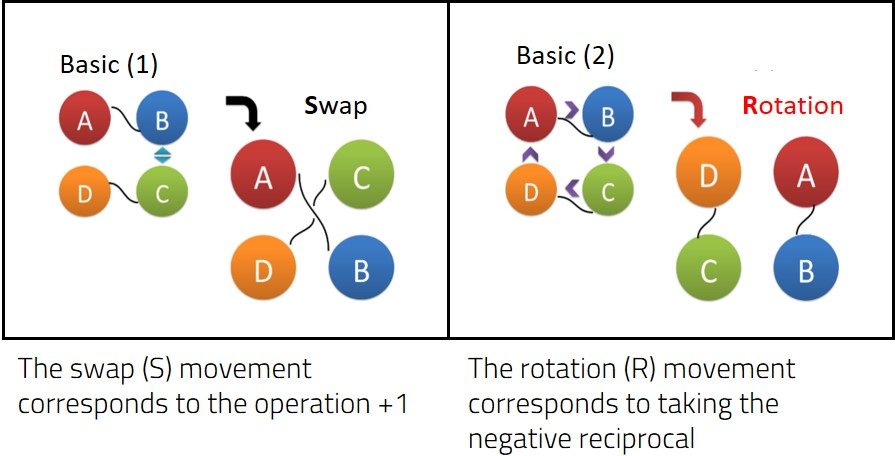
Topology is often excluded from educational programs due to its complex formalism, but, at basic levels, it is a rich, interesting topic that is very suitable for games: false and true knots, the cutting of Möbius strips, folded papers, holes, puzzle games, and magic tricks are all examples. Here, the concept of Conway’s rational tangles[1] is used to propose a ‘dance’ based on simple movements of four people holding ropes.[2] While they’re swapping their positions, a tangle forms between their ropes. To untie the knot, it is necessary to assign rational numbers to knots and operations to each dance step. Using only fraction arithmetic, the knots will finally be untied!

In secondary schools, it could be proposed as a team competition to practise arithmetic, while, in primary schools, it could be used without the more complex mathematics as a precoding activity.
The mathematical field of topology turns out to be rather intuitive and stimulating at a playful level, mainly with the aid of commonly used objects, such as ropes, scarfs, earphone cables, and doughnuts.
The general aim of this activity is to introduce simple elements of topology and open the mind to a vision of forms different from those proposed by geometry or algebra. Topology deals with connections between points of an object, to give mathematical descriptions based to the presence of ‘holes’, ‘continuity’, faces and surfaces, nodes and overlaps, the concepts of internal and external, and borders. Topology is a complex mathematical field, but these intuitive concepts can also be used to give a sort of playful ‘order’ to objects and affinities between different objects, through continuous transformations, such as knots, tangles, and cutting with scissors.
These activities can be carried out in one or two lessons, depending on how much time is taken for discussion and recap of mathematical topics. They are described at a suitable level for students aged 11–16; however, they can be adapted for students aged 17–19 too. They can be used to simply introduce the topology environment; to review/consolidate the teaching of fractions and simple arithmetic; or as a starting point to go deeper into the topic, finding rules and connections between knots and algebra. More detail on how to adapt the activity for different age groups and incorporate it into the curriculum can be found in the supporting material.
Firstly, we introduce some simple and intuitive topological concepts using simple games and tricks. Additionally, if teachers would like to present some background to topology, simple video introductions to topology and knots can be found in the Resources section.


In this activity, pairs of students hold onto either end of pieces of rope and then ‘dance’ specific movements to create knots. They then learn how these dance moves can be assigned mathematical functions, thus allowing the knot and its solution (untying) to be described mathematically.
Try the dance sequences on your own with two strings and four weights tied to the ends!

The knot obtained thus corresponds to a rational number (in the previous example, it corresponds to 7/3). Now students have to search for a sequence of operations that will eventually lead back to zero.
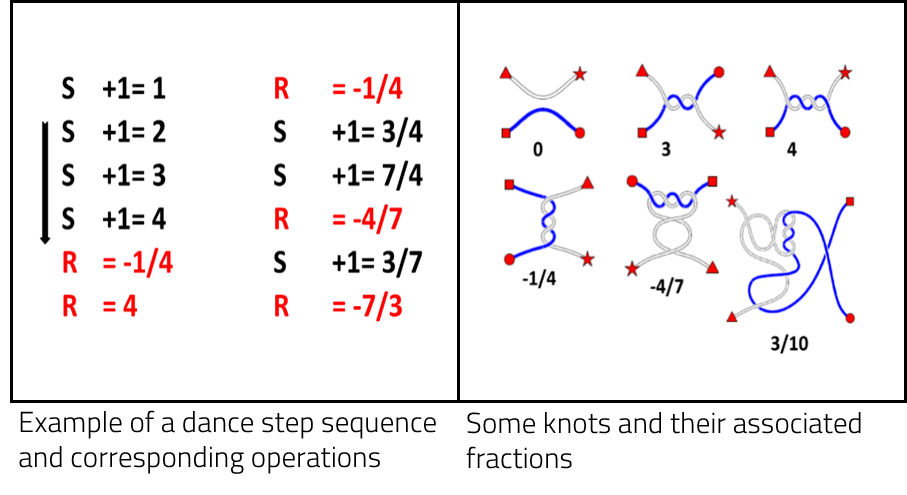
A nice variation is a team competition: the teacher gives the initial steps, and the students have to decide on the best algorithm to untie the knots. When the music is turned on again after the knots are checked, the first team to untie the knot wins.
Considering that there is no single solution algorithm, most teams should be able to untie the knot, but there is still a shortest algorithm, so the fastest team could win. Let students compete on the aspect of optimization of the procedure, which is a more purely computational skill.
Overall, the activities can be used more generally to stimulate problem solving and to demonstrate how mathematics can be used to describe real-world phenomena. However, they can also be used to explore more specific curriculum topics in an engaging context, such as computational thinking, operations with fractions (sum, inverse, opposite sign), computational thinking, dimensionality (e.g., lines versus surfaces), nodes, rational numbers, solving equations, and algorithms.
[1] Goldman JR, Kauffman LH (1997) Rational tangles. Advances in Applied Mathematics, 18: 300–332. doi: 1.1006/aama.1996.0511
[2] Davis T (2017) Conway rational tangles: http://www.scienceinschool.org/wp-content/uploads/2023/05/Tom-Davis-tangles.pdf
Adapting the activity to different age groups
Download this article as a PDF

Sketch graphs from ‘story’ videos of everyday events to help students understand the basic features of graphs and how to interpret…

Do you have more than the average number of ears? Is your salary lower than average? When will the next bus arrive? Ben Parker attempts to convince…
Do you find the binary system complicated? With this activity, your students will find it as easy as…