Verdraaide leugens Understand article
Vertaald door Carolien de Kovel. Hebt u meer dan het gemiddelde aantal oren? Is uw salaris lager dan gemiddeld? Wanneer komt de volgende bus? Ben Parker probeert ons te overtuigen van het nut van statistiek – indien correct toegepast.

aantal oren?
Figuur met dank aan Lisa Kyle
Young/iStockphoto
Of het nu de schrijver Mark Twain was of de politicus Bejamin Disraeli die voor het eerst het gedachte uitsprak dat er drie soorten onwaarheden zijn – “leugens, verdomde leugens en statistiek”- datzelfde gevoel heerst nog steeds. Statistici zijn manipulatieve, verraderlijke types, erop uit om onze geest te vervuilen met betekenisloze en misleidende informatie die ons ertoe brengt om te stemmen voor hun favoriete politieke partij, hun aantoonbaar effectieve huidcrème te gebruiken of het kattenvoer te kopen dat hun eigen huisdieren het liefst eten. Voor mij, als statisticus, wordt het tijd om een paar mythen te ontzenuwen.
Precies 96.4% van onze moderne wereld draait om statistiek en hoewel er ook schokkend slechte statistiek rondwaart, hoop ik u ervan te kunnen overtuigen dat in de meeste gevallen de fout ligt in de presentatie ervan.
(V)ooruit
Ik zou zonder aarzelen met u, mijn beste lezer, willen wedden dat u meer dan het gemiddelde aantal oren heeft. Waarom? Laten we aannemen dat er zes miljard mensen op onze dichtbevolkte planeet wonen, van wie meer dan 99% twee oren heeft. Er zijn een paar bijzondere mensen die, door een ongeval of een aangeboren afwijking één oor of helemaal geen oren hebben. Voor zover ik weet zijn er geen mensen met drie oren (Captain Kirk uit de televisieserie Star Track is helaas verzonnen, maar hij had drie oren: een linkeroor, een rechteroor en tenslotte een middenvoor-oor). Als we het gemiddelde berekenen (alle oren optellen die de mensheid momenteel bezit en dat delen door het aantal mensen), dan krijgen we het sommetje:
Iets minder dan 12 miljard/6 miljard
Wat iets minder is dan twee. Dit betekent dat, aangezien veruit de meeste mensen in de wereld twee oren hebben, ze iets meer dan het gemiddelde toebedeeld hebben gekregen, dus ik zou die weddenschap winnen.
Wat betekent dat?
Wel, dit is natuurlijk alleen maar een statisticus die pedant doet. Er zijn echter voorbeelden bij de vleet die maar ietsje minder onzinnig zijn. Statistieken over hoe een bepaalde groep mensen minder verdient dan een bepaald percentage van het gemiddelde nationale inkomen worden als voetballen heen en weer geschopt in de politiek. Het gebeurt maar al te vaak dat we commentaren lezen in de kranten over hoe schandalig het is dat mensen maar een x percentage verdienen van het gemiddelde nationale inkomen en dat dat allemaal de schuld is van de (Britse) Labour-regering, van het eerdere Conservative kabinet, de Europese Unie of zonnevlekken.
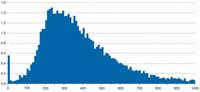
per huishouden 2004/2005:
Aantal individuen
(miljoenen), Groot-Brittanni?.
Bron: ?Housholds below
Average Income (HBAI)
1994/95-2?4/05?, Department
for Work and Pensions ofwel
?Huishoudens onder het
gemiddelde inkomen
1994/95-2?4/05?, DWP
De verdeling van inkomens, volgens het UK Department for Work and Pensions (Britse departement voor werk en pensioenen) (zie de afbeelding hierboven), is zodanig dat er relatief weinig mensen zijn die enorm veel geld verdienen (helaas vallen statistici niet in deze hoge-inkomensgroep). Dit betekent dat het gemiddelde inkomen, dat door het Departement is berekend als £427 per week voor een stel zonder kinderen (DWP, 2006), veel meer is dan wat de meerderheid van de mensen verdient, geheel parallel met het voorbeeld hierboven van het aantal oren. Een paar uitzonderlijke mensen, of ze nu minder dan twee oren hebben of gigantisch veel geld verdienen, verschuiven het gemiddelde weg van de situatie van de meerderheid van de mensen.
Natuurlijk hadden mensen al gauw door dat dit veelgebruikte gemiddelde, berekend door alles op te tellen en dan te delen door het aantal dingen dat je had opgeteld, en wat eigenlijk het ‘rekenkundig gemiddelde’ heet, gemakkelijk verkeerd geïnterpreteerd kon worden. Daarom wordt vaak het concept van de ‘mediaan’ gebruikt in de praktijk. Als we alle mensen in Groot-Brittannië op een rij zouden zetten op volgorde van hun inkomen, dan zou het mediane salaris het bedrag zijn dat de persoon die precies in het midden staat verdient. Het mediane inkomen, zo’n £349 in dit voorbeeld, geeft meestal een beter idee van wat ‘normaal’ is.
Nu we zijn uitgekomen op wat gezond verstand, kunnen we er toch wel van uitgaan dat iedereen dit tamelijk basale probleem begrijpt dat ligt in het overbrengen van ideeën met behulp van gemiddelden? Tenslotte is het toch zeker de rol van een goede journalist om ideeën te nemen en de waarheid dan zo te presenteren dat het publiek het kan begrijpen.
Helaas, feitelijke juistheid en correcte interpretatie van gegevens verkopen soms geen kranten of maken soms niet het gewenste politieke punt.
De kreukels gladstrijken

was tevreden
Figuur met dank aan Al
Wekelo/iStcokphoto
Erger dan journalisten, maar nog niet zo erg als politici, zijn adverteerders. Een recente televisiereclame van een cosmetisch bedrijf beweert dat over hun nieuwste anti-rimpelcrème 8 van de 10 klanten tevreden zijn, gebaseerd op een onderzoek onder 134 mensen. We kunnen de kleine steekproef misschien nog wel vergeven – en zelfs de afronding (134 x 8/10 = 107.2), die inhoudt dat ze ergens 0.2 klant moeten hebben gevonden om de crème te proberen – maar de cruciale vraag is hoe ze het onderzoek hebben uitgevoerd.
Het lijkt me dat het dubieus is als je 134 klanten vraagt of het product ze bevalt – als die mensen al klant zijn, en ze hebben het product vrijwillig gekocht, dan is dat misschien niet de eerlijkste steekproef die je had kunnen hebben. Waarom zou iemand iets kopen als het product hem (haar) niet bevalt? In de netste wetenschappelijke tests, zou men graag zien dat de prestaties van deze crème objectief worden vergeleken met die van merk X, of een placebo, om te zien of willekeurige mensen een positief effect van de crème ondervinden.
Adverteren op zich is geen probleem: filosofen beweren dat adverteren een essentieel onderdeel is van een sterke democratie. Het is prima als adverteerders mensen van hun product op de hoogte stellen en de voordelen ervan benadrukken. Echter, het is niet acceptabel als een dun vernislaagje van wetenschap rond de reclame wordt aangebracht. Hoewel het slim is gebracht, als de methode niet wordt uitgelegd, zegt dat getal ‘ 8 van de 10’ helemaal niets. Het is net zo onzinnig als zeggen, dat “onze auto een topsnelheid heeft van 800 km per uur”, zonder daarbij te vermelden dat die snelheid gehaald wordt als je meet hoe snel de auto uit een vliegtuig valt: het is wel waar, maar het is misleidend.
Drie tegelijk
Misschien is het niet helemaal eerlijk om alle schuld bij de boodschappers te leggen in plaats van bij de statistiek zelf. Er zijn best wat echte, lastige, niet-intuïtieve feiten die door de statistiek worden uitgespuugd en waarvan de waarheid maar erg moeilijk te vatten is. Stel dat u op de bus staat te wachten en u kijkt op het rooster, dat u vertelt, mits het niet door vandalen gemold is, dat er vijf bussen per uur komen. Hoe lang denkt u op uw bus te moeten wachten?
Gewone logica vertelt ons dat als er 5 bussen per uur komen, dat dan de gemiddelde (sorry rekenkundig gemiddelde) tijd tussen twee bussen 12 minuten is. Als we dus aannemen dat u bij de halte aankomt op een willekeurige tijd tussen twee bussen, dat u dan kunt verwachten dat u zes minuten moet wachten. Logisch, maar helaas over het algemeen niet correct.
We weten dat bussen niet op de minuut rijden. Ze verlaten het depot wellicht op tijd, maar allerlei toevalsfactoren beïnvloeden hun voortgang op verschillende manieren, dus we kunnen verwachten dat het patroon waarin ze arriveren wat varieert. Welke distributie we daarvoor aannemen kan variëren – we kunnen bijvoorbeeld aannemen dat de wachttijden tussen twee bussen exponentieel verdeeld zijn -, maar het belangrijkste feit is dat de bussen niet strikt regelmatig komen. Laten we nu weer aannemen dat u op een willekeurig moment bij de halte arriveert – hoe lang moet u dan op een bus wachten?
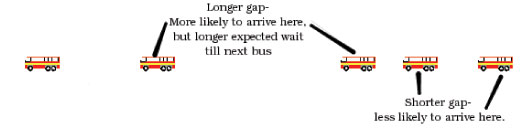
Figuur met dank aan Ben Parker
We hebben meer kans bij de halte te arriveren tijdens een groot tijdsgat tussen twee bussen dan tijdens een klein tijdsgat – aangezien zo’n groot gat nu eenmaal meer tijd inneemt dan een klein tijdsgat. Als we dus in zo’n groter gat arriveren, dan weten we ook dat de periode tussen twee bussen meer dan 12 minuten is (ook al zijn er nog steeds 5 bussen per uur) – dus de gemiddelde wachttijd, gegeven dat we op elk willekeurig punt in het tijdsgat kunnen arriveren met dezelfde waarschijnlijkheid, is meer dan 6 minuten.
Dit staat bekend als de inspectieparadox, en het valt niet mee om je hersens eromheen te buigen. Het is echter een echt fenomeen en het wordt gebruikt door verkeersplanners en logistieke onderzoekers, die bijvoorbeeld moeten uitzoeken wat de handigste manier is om rijen in het postkantoor op te stellen, hoewel ze het soms prompt vergeten.
Is het dan verkeerd dat de busmaatschappijen beweren dat ze ongeveer elke 12 minuten een bus laten rijden? Ik vind eigenlijk van wel, hoewel het wat lastig is om al de smerige details van de inspectieparadox uit te leggen; in dit geval kunnen we misschien wel wat statistische slordigheid vergeven.
Conclusies
In het algemeen is statistiek vrij intuïtief en de gevallen die moeilijk te bevatten zijn, zijn zeldzaam. In het algemeen moet een lezer:
- Uitzoeken wie de data presenteert en wat hij/zij daarmee beoogt.
- Indien mogelijk, de methode achterhalen waarmee de steekproef getrokken is: of de gegevens komen van een geschikte representatieve steekproef uit de gemeten populatie en of de test op een nette manier is uitgevoerd. Zijn de juiste dingen vergeleken en is de juiste vraag gesteld?
- Kritisch kijken naar gemiddelden en percentages en erover nadenken hoe extreem de getallen nu echt zijn, en wat je dan eigenlijk zou verwachten dat ze waren. In het bijzonder, er niet van uitgaan dat gemiddelden typerend zijn voor de dataset.
Statistiek is een krachtig en handig werktuig in de juiste handen en we moeten de mensen de mogelijkheid geven om het te begrijpen. We moeten er ook voor zorgen dat wat basaal onderwijs in statistiek, vooral met betrekking tot het interpreteren van advertenties, aan elk kind op school wordt aangeboden. Op zijn minst tot het moment dat journalisten, de reclamewereld, en de mensen die ze aansturen wat verstand hebben van statistiek en vooral hoe je die moet presenteren, zal de wereld niet de beste huidcrème kopen of het beste kattenvoer voor zijn huisdieren, die vrijwel allemaal meer dan het gemiddelde aantal oren hebben.

References
- DWP (2006) Households Below Average Income (HBAI) 1994/95-2004/05. London, UK: Department for Work and Pensions
- Dit artikel is eerder verschenen in Plus, een gratis online tijdschrift dat een blik biedt de wereld van de wiskunde: http://plus.maths.org. “Damn lies” (Verdraaide leugens) was tweede in de algemene publiekscategorie van de Plus-prijs van nieuwe auteurs.
Review
Dit artikel biedt een geestige blik op hoe statistiek wordt misbruikt in het leven van alledag. Het zou te begrijpen moeten zijn voor leraren, studenten en algemene lezers uit de hele wereld. Op school zou het gebruikt kunnen worden als een inleiding in statistiek en waarschijnlijkheidsrekenen om leerlingen ertoe aan te zetten na te denken over hoe statistiek en waarschijnlijkheid kunnen worden gebruikt en misbruikt.
Ik vind vooral de komische koppen en de humor in het artikel leuk – soms overduidelijk, soms subtiel.
Marco Nicolini, Italië





