Podstawy balistyki: modelowanie torów dla rzutów Teach article

Author(s): Elias Kalogirou, Ian Francis

Tłumaczenie Grzegorz Glubowski. Niekiedy sprawiają uczniom trudność obliczenia związane z torami rzutów. Model stworzony przez Elias Kalogirou pozwala łatwo obrazować ich trajektorie. Dodatkowo, Ian Francis proponuje szersze zastosowania dla tego modelu na lekcjach.

Budowa modelu

Dzięki uprzejmości yenwen /
iStockphoto

Wprowadzenie

Rzucona lub uderzona piłka, wystrzelona z broni palnej kula lub zrzucony z mostu kamień mają coś wspólnego – w sensie fizycznym są one pociskami. Określenia tego używa się w odniesieniu do dowolnego obiektu o znanej prędkości początkowej poruszającego się wzdłuż określonego toru, na którego kształt mają wpływ: grawitacja i opór powietrza. Zaprojektowałem model, który ma ułatwić obrazowanie torów ruchu, a także pozwolić studentom na szacowanie składowych poziomych i pionowych rzutu. Opór powietrza nie jest w tym modelu uwzględniony.

Budowa

Materiały

  • Statyw
  • Drewniana listewka, przynajmniej 105 cm długości
  • Wiertarka oraz wiertła
  • Cienki sznurek, najlepiej kolorowy
  • 20 drewnianych lub plastikowych koralików o średnicy 14 mm z otworem w środku, przez który można przewlec sznurek
  • 20 spinaczy biurowych
  • Miara taśmowa
  • Nożyczki

Wykonanie

  1. Przymocuj linijkę do statywu
    tak, aby było można
    regulować kąt pomiędzy nimi

    Wywierć otwór w listewce, w niewielkiej odległości od jej końca (u mnie 3 cm). Później wykorzystasz go do przymocowania listewki do statywu.

  2. Wywierć 20 otworów (ja wybrałem średnicę 2,5 mm) w odstępach co 5 cm mierząc od otworu wykonanego według opisu z punktu 1.
  3. Przymocuj listewkę do statywu. Ponieważ potrzeba zapewnić możliwość regulowania kąta pomiędzy nimi, zamocuj listewkę na sworzniu. Ja użyłem łącznika i dwóch podkładek (zobacz obraz).
  4. Dla każdego z 20 otworów oblicz potrzebną długość sznurka (Tabela 1). Odmierz wyliczoną długość sznurka, dołóż około 5 cm ekstra na mocowanie sznurka do koralika oraz do listewki i odetnij.
  5. Dla każdego kawałka sznurka przywiąż u jednego jego końca koralik, a drugi koniec przewlecz przez odpowiedni otwór w listewce i zamocuj na nim spinacz biurowy, który będzie spełniać rolę ogranicznika (zobacz obraz). Nie używaj taśmy klejącej (zamiast spinaczy), ponieważ stopniowo będzie się luzować.
  6. Zamocuj sznurki do linijki
    przeplatając ich końce przez
    spinacze biurowe
    Dzięki uprzejmości Elias’a
    Kalogirou

    Wyreguluj długości sznurków tak aby dokładnie odpowiadały wyliczonym.

Przygotowanie kompletnego modelu zajęło mi około dwie godziny.

Obliczanie długości sznurków

Tor rzutu – model
Zdjęcia dzięki uprzejmości
Elias Kalogirou

Przed przystąpieniem do obliczania długości sznurków, powinieneś rozumieć co nasz model przedstawia. Wyobraź sobie, że w chwili początkowej wystrzeliłeś ze stałą szybkością pocisk (brak przyspieszenia poziomego) z miejsca, w którym znajduje się sworzeń (łączący linijkę i statyw) w kierunku, w którym wycelowana jest linijka.

Model demonstruje dwie właściwości toru. Po pierwsze, kierunek w którym jest wycelowana linijka, pokazuje kierunek w którym pocisk kontynuowałby lot, gdyby nie było grawitacji.

Po drugie, sznurki demonstrują wpływ przyspieszenia grawitacyjnego (g). Gdyby w chwili początkowej pocisk spadł ze sworznia (spadek pionowy bez prędkości początkowej), długość sznurka na którym wisi pierwszy koralik pokazałaby odległość, o jaką pocisk opadłby po czasie t; długość sznurka na którym wisi drugi koralik pokazałaby odległość, o którą pocisk opadłby po 2t; itd. (Tabela 1).

Grawitacja działa identycznie podczas rzutu z niezerową prędkością początkową, zatem gdy zamiast pozwolić pociskowi spaść, wyrzucisz go poziomo, będzie opadał o tyle samo w kolejnych odstępach czasu t.

Dla prędkości początkowej większej od zera, długość pierwszego sznurka jest odległością o jaką pocisk opada po czasie t, drugiego sznurka odległością o którą pocisk opada po 2t, itd. Położenie koralików przedstawia paraboliczną trajektorię rzutu, a kąt między linijką i statywem początkowy kąt rzutu.  

Położenia 20 koralików, wiszących w odstępach co 5 cm, ukazują pozycje pocisku w 20 równoodległych w czasie położeniach – pierwszy koralik położenie po czasie t, drugi koralik (na linijce 5 cm dalej) po czasie 2t, itd., aż do ostatniego koralika, który pokazuje pozycję pocisku po czasie 20t.

Model przedstawia trajektorie rzutów o stałej prędkości poziomej (także zerowej – po umieszczeniu listewki pionowo, czyli równolegle do statywu) i stałego przyspieszenia w kierunku pionowym. Jeśli wybierzesz wartość t, przytniesz odpowiednio sznurki i zbudujesz model, otrzymasz możliwość demonstrowania możliwych torów dla wybranej wartości t, jak też szczególnej prędkości początkowej i przyspieszenia grawitacyjnego – w zależności od kąta ustawienia linijki, przy pominięciu oporu powietrza. Pytanie jak dokładnie model ten odzwierciedla rzeczywistość może być punktem wyjścia do interesującej dyskusji.

Długość najkrótszego ze sznurków, jest dla czasu t obliczana na podstawie:

a = ½ g× t2.

By obliczyć długość a, określ wpierw maksymalną długość sznurka dla koralika numer 20, który będzie 100 cm dalej, a która odpowiada długości 400a (Tabela 1). Nasz najdłuższy sznurek (400a) miał 145 cm, zatem a = 0.3652. Możesz wyliczyć długości sznurków dla wszystkich 20 koralików, korzystając z kolumny ‘String length’ – „długość sznurka” w tabeli 1 (przy odcinaniu nie zapomnij o dodatkowych 5 cm – krok 4 powyżej.

Czas Odległość wzdłuż listewki (cm) Tracona wysokość podczas opadania Długość sznurka Długość sznurka jeżeli a = 0.3652 (cm)
Tabela 1: Opadanie pionowe przy wykorzystaniu modelu
t 5 ½ g t2 a 0.3652 
2t 2 x 5=10 ½ g (2t)2 4a 1.4608
3t 3 x 5=15 ½ g (3t)2 9a 3.2868
4t 4 x 5=20 ½ g (4t)2 16a 5.8432
… … … … …
20t 20 x 5=100 ½ g (20t)2 400a 145

Użycie modelu podczas lekcji

Budowa modelu jest ważnym elementem procesu dydaktycznego. Produkt finalny może być dodatkowo wykorzystany do dalszej pracy. Można go użyć do  demonstrowania rzutów poziomych lub pionowych, a także skierowanych pod dowolnym kątem pośrednim. Poniżej podaję kilka sugestii dotyczących jego wykorzystania – nie wyczerpuje to wszystkich możliwości.

Eksperyment 1

W tym eksperymencie, uczniowie dowiadują się, że składowe pozioma i pionowa toru są niezależne od siebie, przy czym prędkość pozioma pozostaje stała podczas całego „lotu”.

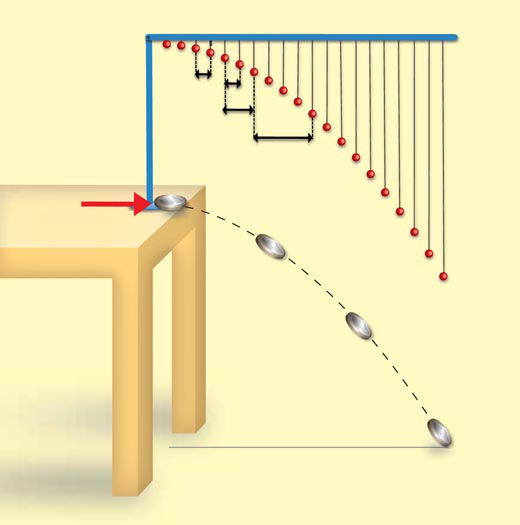
  1. Uczniowie ustawiają listewkę poziomo (90 stopni względem statywu). Koraliki wskazują teraz pozycje pocisku, któremu nadano początkową prędkość poziomą, ale nie ma początkowej prędkości pionowej (jak dla monety poziomo zrzuconej ze stołu).
  2. Uczniowie szacują jak długo pocisk przemieszczałby się z pozycji startowej (sworzeń) do pierwszego koralika (lub od dowolnego koralika do kolejnego po nim). Jakikolwiek czas różny od jednej sekundy będzie do przyjęcia.
    Spróbujmy następnie określić ten czas dokładniej – co oczywiście zależeć będzie od tego, z jaką szybkością ciało jest wyrzucane.
  3. Niech uczniowie wyrzucają monetę wzdłuż modelu próbując spowodować by odległość, którą pokonuje ona w kierunku poziomym była zbliżona do długości listewki, oraz mierzą czas upływający do momentu zetknięcia się monety z podłożem. Podzielenie tego czasu przez liczbę koralików, które moneta minęła, pozwoli oszacować przedział czasu dla przelotu pomiędzy kolejnymi koralikami, przy pominięciu oporu powietrza. Im dłuższa trajektoria lotu, tym mniej znaczący powinien być błąd wyznaczenia tego czasu.
  4. Znając wartość tego czasu, niech uczniowie obliczą wartość prędkości poziomej dla kilku par koralików (zarówno sąsiadujących ze sobą jak i położonych nieco dalej od siebie, np.: pomiędzy 3 i 4 koralikiem, następnie pomiędzy 3 i 15 koralikiem (upewnij się, że uczniowie stosują odpowiednio dłuższy przedział czasu gdy biorą pod uwagę nie sąsiadujące ze sobą pary koralików) wykorzystując fakt, że prędkość pozioma = poziome przemieszczenie / przedział czasu:
    vpoz = spoz / t

Upewnij się, że uczniowie mierzą odległość poziomą pomiędzy parami koralików, nie odległość po przekątnej. Jeśli model został zbudowany poprawnie, powinni otrzymać stałą wartość prędkości poziomej.

Uczniowie mogą być zaznajomieni z pojęciem prędkości średniej, natomiast w mniejszym stopniu z ideą dzielenia przemieszczenia na małe przedziały czasowe. Dlatego mogłoby być użyteczne obliczenie średniej prędkości poziomej = całkowite przemieszczenie poziome / całkowity czas. Powinna być oczywiście równa wartościom prędkości wyliczonym na podstawie położenia koralików.

  1. Niech uczniowie objaśnią jakie założenie przyjmujemy gdy twierdzimy, że prędkość pozioma pocisku jest stała. Prawidłowe wyjaśnienie powinno stwierdzać, że można pominąć opór powietrza.
Przygotowanie do eksperymentu nr 1. Uczniowie powinni zmierzyć poziomą odległość pomiędzy sąsiadującymi oraz nie sąsiadującymi parami koralików i czas  ruchu monety wyrzuconej wzdłuż modelu
Dzięki uprzejmości Marlene Rau i Nicola Graf

Eksperyment 2

W tym doświadczeniu uczniowie dowiadują się, że prędkość pozioma dla rzutu z niezerową początkową prędkością w kierunku pionowym (np. pod kątem) jest stała, ale że jest ona mniejsza niż w przypadku rzutu bez początkowej prędkości pionowej. (jak to było w eksperymencie nr 1).

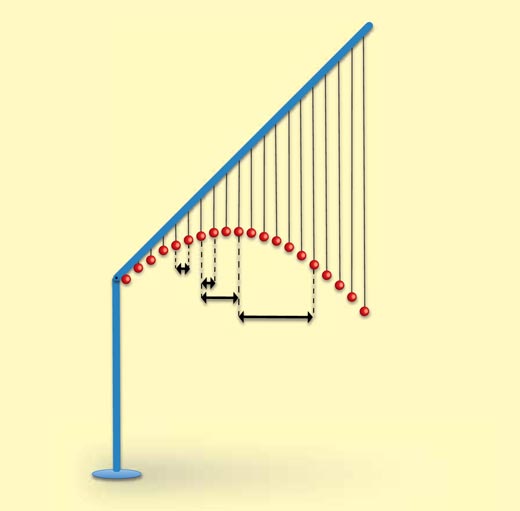
  1. Ustaw listewkę pod kątem względem poziomu. Sugeruję zastosowanie dużego kąta, aby uczniowie zaobserwowali znacząco inne przemieszczenie poziome niż w eksperymencie nr 1.
  2. Stosując wartość t obliczoną w eksperymencie nr 1 lub wartość t użytą przy budowie modelu uczniowie powtarzają obliczanie prędkości poziomej, jak w punkcie 4 eksperymentu nr 1.

Ponownie, jeśli model został zbudowany starannie, uczniowie powinni stwierdzić, że odległość pozioma pokonywana w równych odstępach czasu jest stała, ale oczywiście mniejsza niż dla rzutu bez początkowej prędkości w kierunku pionowym (eksperyment nr 1) – sznurki odpowiednich koralików będą bliżej siebie.

Przygotowania do eksperymentu nr 2. Uczniowie mierzą odległość poziomą pomiędzy sąsiadującymi i nie sąsiadującymi koralikami / parami sznurków – która okaże się mniejsza niż w eksperymencie nr1
Dzięki uprzejmości Marlene Rau

Eksperyment 3

W tym eksperymencie uczniowie badają odległości pionowe pokonywane w jednakowych odstępach czasu dla rzutu bez początkowej prędkości pionowej (jak w eksperymencie nr 1). Ten eksperyment przeznaczony jest dla tych uczniów, którzy nie byli zaangażowani w budowę modelu, choć jego przeprowadzenie może być pożyteczne dla wszystkich.

  1. Umocuj listewkę poziomo.

Zmiana składowej pionowej prędkości określa przyspieszenie (a). Z równania
F = m× a wiemy, że dla uzyskania przyspieszenia potrzebna jest siła – w tym przypadku działająca na obiekt siła grawitacji. Ponieważ jest to siła stała, z równań dla ruchu jednostajnie przyspieszonego otrzymujemy

pionowo pokonywana odległość (s) = (u×t) + (½ a× t2)

gdzie u jest prędkością początkową.

Ponieważ prędkość początkowa (u) jest równa zero, (u× t) można pominąć, a skoro ½ a jest wielkością stałą równanie stwierdza, że przemieszczenie pionowe jest proporcjonalne do kwadratu czasu. Warto wspomnieć, że przyspieszenie (a) oraz przyspieszenie ziemskie (g) są w tym przypadku jednakowe i obie te wielkości stanowią przyspieszenie w swobodnym spadku.

  1. Niech uczniowie obliczą czas „przelotu” do każdego koralika (w miejscu połączenia t = 0) – dla pierwszego koralika będzie to zatem 1t, dla drugiego 2t, itd. (Tabela 1), stosując wartość t przyjętą dla modelu.
  2. Niech uczniowie zmierzą długości sznurków dla różnych pozycji – jeśli brak czasu dla zmierzenia wszystkich 20, niech zmierzą przynajmniej najkrótszy, najdłuższy i przynajmniej trzy inne – oraz zanotują wartości. Są to dla tych punktów pokonane odległości pionowe (tracona wysokość „lotu”).
  3. Niech uczniowie przedstawią graficznie wartość traconej wysokości w czasie całkowitym podniesionym do kwadratu (np. t2 dla punktu nr 1, (2t)2 dla punktu nr 2, itd.) dla każdej mierzonej pozycji, włączając punkt zero.

Zamiast stosować wartość t przyjętą podczas budowy modelu, uczniowie mogliby zastosować wartość wyliczoną w eksperymencie nr 1. Nawet jeśli nie jest ona zbliżona do wartości przyjętej na początku oczekujemy nadal, że wykres będzie linią prostą, przynajmniej poza drugim punktem wykresu.

Eksperyment nr 4

Ten prosty eksperyment ma ukazać fakt że składowe poziome i pionowe prędkości są niezależne od siebie.

  1. Ustaw linijkę pod kątem 45 stopni do statywu.
  2. Uczniowie powinni zauważyć, że przemieszczenia pionowe pozostały nie zmienione to jest, że odległość od dowolnego koralika do listewki będzie zawsze taka sama, niezależnie od kąta położenia linijki, ponieważ długości sznurków nie zmieniły się.

Możliwe rozwinięcia

Oto pytania które można postawić uczniom:

  • Pod jakim kątem względem poziomu zasięg będzie największy? Co będzie, jeśli grunt nie jest płaski?
  • W jaki sposób należałoby zaadoptować model dla tych planet, na których przyspieszenie grawitacyjne jest mniejsze niż 9.8 m/s2 na Ziemi?
  • Czy uczniowie potrafią określić wartości składowych pionowych chwilowych prędkości, grupując parami odczyty podczas gdy listewka jest ustawiona pod pewnym kątem? Czy potrafią wykorzystać te wartości dla stwierdzenia na ile dobrze ten model ukazuje, że przyspieszenie grawitacyjne ma wartość 9.8 m/s2?
  • Czy przyspieszenie w kierunku pionowym zmienia się w zależności od kąta pod jakim zamocowano linijkę?

Resources

  • Freier GD, Anderson FG (1981) Demonstration Handbook for Physics (2nd edition). College Park, MD, USA: American Association of Physics Teachers. ISBN: 9780917853326
  • Animację rzutu można obejrzeć na: www.phy.hk/wiki/englishhtm/ThrowABall.htm
  • Wikipedia zawiera dobre objaśnienia rzutów, w szczególności ‘Angle θ required to hit coordinate (x,y)’ – „Kąt θ potrzebny by wcelować w punkt o współrzędnych (x,y)”: http://en.wikipedia.org/wiki/Trajectory_of_a_projectile

Author(s)

Elias Kalogirou był 10 lat nauczycielem fizyki i naprawdę lubi uczyć swych uczniów rzeczy, które mogą zastosować w codziennym życiu. Odpowiada za działanie regionalnego centrum laboratoryjnego nauk fizycznych w Pyrgos, Ilia, Grecja, w którym nauczyciele szkół średnich mogą doskonalić zawodowo poznając metody eksperymentalne w nauce fizyki, chemii i biologii.

Ian Francis nauczał w szkole średniej i na poziomie zaawansowanym przez około 20 lat, głównie w Londynie, UK, oraz na południu Anglii. Jest również egzaminatorem egzaminów państwowych (GCSE oraz A levels). Autoryzował materiały dydaktyczne dla różnych projektów w UK włączając ‘I’m a scientist, get me out of here!’ i SEPnet (South East Physics Network).

Review

Idea leżąca u podstaw budowy modelu proponowanej w tym artykule jest niezwykle kreatywna, a uczniowie uczą się poprzez aktywne uczestnictwo, wykorzystując po drodze wiele różnych umiejętności. Gotowy model będzie również służył jako pomoc wizualna dla omawianej na lekcjach teorii. Ważne uzupełnienie stanowi zestaw ćwiczeń, które można wykonać podczas lekcji.

W zależności od uczniowskich umiejętności, nauczyciele mogą pozwolić im na samodzielne odkrycie teorii leżącej u podstaw eksperymentu lub też poprowadzić ich na tej drodze.

Ćwiczenie mieści się w programie nauczania fizyki, jako część nauki o rzutach, zagadnieniu zawartym w większości europejskich programów. Można je traktować interdyscyplinarnie, ponieważ budowa modelu wymaga wykorzystania umiejętności projektowych i technicznych. Umiejętności matematyczne również są tutaj wykorzystywane.

Jürgen Azzopardi, Malta

License

CC-BY-NC-SA

Download

Download this article as a PDF