Un modello per lo studio del moto dei proiettili Teach article
Tradotto da Giulio Sinno - Liceo scientifico L.Mossa - Olbia. Gli studenti, nello studio della cinematica, spesso trovano difficoltà nel calcolo delle traiettorie dei proiettili. Con l’aiuto del modello di Elias Kalogirou queste traiettorie possono essere visualizzate facilmente.…
Realizzazione del modello

concessa da yenwen /
iStockphoto
Introduzione
Quando si colpisce una palla, si spara un proiettile con una pistola o si lancia un sasso da un ponte, gli oggetti ‘volanti’ in questione hanno una cosa in comune: da un punto di vista fisico sono tutti dei proiettili. Il termine proiettile è usato per tutti quegli oggetti ai quali viene impressa una velocità iniziale e di conseguenza percorrono una ben definita traiettoria determinata dalla gravità e dalla resistenza dell’aria. Abbiamo realizzato un modello che aiuta a visualizzare queste traiettorie in classe e che permette di studiare le componenti orizzontali e verticali del moto di un proiettile. Bisogna specificare che il modello non tiene conto della resistenza dell’aria.
Realizzazione
Materiali
- Uno stativo con morsetto
- Un righello di legno lungo almeno 105 cm
- Un trapano e relative punte
- Spago sottile, preferibilmente colorato
- 20 palline in plastica o legno di 14 mm di diametro con un foro attraverso il quale sia possibile far passare lo spago
- 20 graffette
- Un metro a nastro
- Un paio di forbici
Procedura
-

Fissare il righello al morsetto
in modo che si possa variare
l’angolo di inclinazioneAd una piccola distanza dalla fine del righello (nel nostro caso 3 cm), fare un foro per inserire un perno che fisserà il righello al morsetto dello stativo.
- Fare 20 fori (noi abbiamo usato una misura di 2.5 mm per il diametro) a intervalli di 5 cm sul righello, il primo dei quali a 5 cm dal foro fatto al punto 1.
- Fissare il righello allo stativo con il morsetto. L’angolo deve essere regolabile: usare un perno e due rondelle (vedere foto).
- Per ciascuno dei 20 fori, calcolare la lunghezza corrispondente della cordicella richiesta (vedere la tabella 1). Lasciare 5 cm in più per ciascuna cordicella, per poterla attaccare alla pallina e al righello, quindi tagliare dal gomitolo di spago le 20 cordicelle.
- Per ciascuna cordicella legare una pallina ad una estremità e fissare l’estremità opposta al righello con una graffetta (vedere foto). Evitare l’uso di nastro adesivo al posto delle graffette in quanto col tempo tende a staccarsi.
-

Fissare le cordicelle al
righello utilizzando le
graffette
Immagine gentilmente
concessa da Elias KalogirouRegolare la lunghezza delle cordicelle ai valori calcolati
Il modello ora è completo. Per regolarvi noi abbiamo impiegato circa due ore per costruirlo.
Calcolo delle lunghezze delle cordicelle
Per poter calcolare le lunghezze delle cordicelle, dobbiamo capire cosa sta rappresentando il modello. Immaginate di sparare un proiettile all’istante zero a velocità costante (accelerazione orizzontale nulla) dall’origine (nel nostro caso il punto di giunzione del righello con il morsetto) lungo la direzione del righello.

di un proiettile
Immagine gentilmente
concessa da Elias Kalogirou
Il modello mette in evidenza due aspetti della traiettoria. Primo, la direzione del righello fornisce la direzione lungo la quale il proiettile continua a volare se non c’è gravità.
Secondo, le cordicelle rappresentano l’effetto della gravità (g). Se lasciamo cadere il proiettile dall’origine all’istante zero (caduta verticale a velocità iniziale nulla), la lunghezza della cordicella della prima pallina fornisce la distanza percorsa dal proiettile in caduta all’istante generico t, quella della seconda pallina la distanza a 2t e così via (vedi tabella 1).
La gravità fornisce lo stesso effetto su un proiettile con una velocità iniziale non nulla, quindi se spariamo un proiettile piuttosto che lasciarlo cadere, esso cadrà ancora alla stessa distanza nell’istante t.
Per una velocità iniziale maggiore di zero, la lunghezza della prima cordicella di nuovo dà la distanza del proiettile che cadrebbe all’istante t, la seconda, la distanza del proiettile che cadrebbe all’istante 2t e così via. Le palline quindi rappresentano la traiettoria parabolica di un proiettile con l’angolo di inclinazione del righello pari all’angolo di partenza del proiettile.
Le posizioni delle 20 palline, appese ciascuna a 5 cm di distanza l’una dall’altra, corrispondono alle posizioni di un proiettile in 20 istanti diversi consecutivi ed equispaziati nel tempo: la prima pallina all’istante t, la seconda (5 cm distante sul righello dalla prima) all’istante 2t e così via, fino all’ultima corrispondente a 20t.
Il modello rappresenta traiettorie a velocità orizzontale costante (compreso lo zero se disponiamo il righello in posizione verticale, parallelo allo stativo) e accelerazione costante verticale. Una volta scelto il valore di t, tagliate le cordicelle e costruite il modello, sarà un modello con quello specifico valore di t, così come anche per specifici valori di velocità e accelerazione (gravità) ad angoli differenti, in base alla posizione angolare del righello, e trascurando la resistenza dell’aria. Quanto il modello si avvicina alla realtà potrebbe essere un interessante argomento di discussione con gli studenti.
La lunghezza della cordicella più corta, all’istante t , si calcola con:
a = ½ g t2.
Per calcolare la sua lunghezza (a), scegliete la massima lunghezza della cordicella della pallina numero 20 la quale è a 100 cm dall’origine, che corrisponde a 400a (vedere tabella 1). La cordicella più lunga che abbiamo usato (400a) era 145 cm, quindi a = 0.3652. Quindi si possono calcolare le lunghezze di tutte le 20 cordicelle da tagliare usando i valori della colonna ‘Lunghezza della cordicella’ della Tabella 1 (non dimenticate di lasciare 5 cm in più, quando tagliate, come detto al punto 4 della procedura).
Come utilizzare il modello in classe
La costruzione stessa del modello costituisce già una valida fase di apprendimento di per sé. Ma il prodotto finale può essere utilizzato ulteriormente per lo studio di traiettorie orizzontali o verticali così come per valori di angoli di gittata intermedi. Di seguito alcuni suggerimenti.
Esperienza numero 1
In questa esperienza gli studenti imparano che le componenti orizzontali e verticali di una traiettoria sono indipendenti nel caso in cui la velocità orizzontale rimane costante durante il volo.
- Chiedete agli studenti di mettere in posizione orizzontale il righello. Le palline ora indicano la posizione di un proiettile che ha una velocità orizzontale costante ma non ha una velocità verticale iniziale (come una moneta colpita lungo un tavolo che poi cade).
- Chiedete agli studenti di stimare il tempo di percorrenza di un proiettile per muoversi dall’origine (il perno) alla prima pallina (o anche da una pallina qualunque a quella successiva). Qualsiasi valore del tempo minore di un secondo andrà bene.
Poi cercheremo di ottenere questo numero più vicino alla reale configurazione, che dipenderà naturalmente dalla velocità iniziale del proiettile. - Invitate gli studenti a colpire una moneta sul tavolo accanto al modello con la velocità giusta per ottenere una gittata (distanza orizzontale) di lunghezza pari a quella del righello e stimare il tempo impiegato. Fate dividere questo intervallo di tempo per il numero di palline sorpassate dalla moneta, si otterrà l’intervallo di tempo approssimato del tempo di volo fra due palline successive, trascurando la resistenza dell’aria. Più lunga è la traiettoria minore dovrebbe essere l’errore sul tempo.
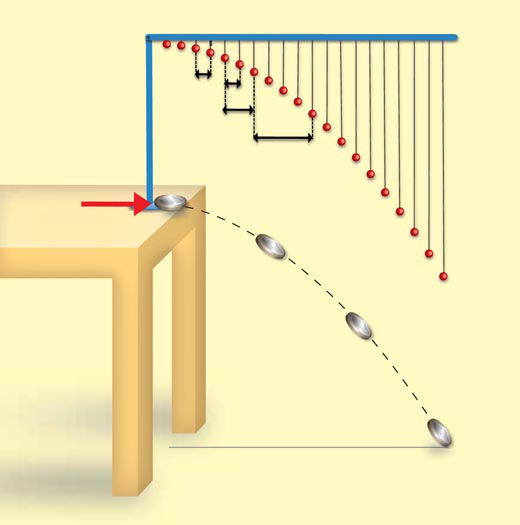
Immagine gentilmente concessa da Marlene Rau and Nicola Graf
- Con questo valore dell’intervallo di tempo, chiedete agli studenti di calcolare la velocità orizzontale per qualche coppia di palline (sia quelle consecutive che non, ad esempio fra la 3 e la 4 e fra la 3 e la 15 – assicuratevi che gli studenti utilizzino l’intervallo di tempo appropriato nel caso di coppie di palline non consecutive), usando velocità orizzontale = spostamento orizzontale/ intervallo di tempo: vhoriz = hhoriz / t.
Assicuratevi che gli studenti misurino la distanza orizzontale fra coppie di palline, non la distanza diagonale. Se il modello è stato costruito accuratamente, dovrebbero trovare la velocità orizzontale costante.
Per gli studenti è familiare la formula della velocità media, ma non così familiare è il concetto di dividere un moto in piccoli intervalli di tempo. Quindi potrebbe valere la pena di far calcolare loro la velocità orizzontale media = spostamento orizzontale totale / tempo totale. Questa dovrebbe naturalmente uguagliare le velocità ottenute dalle posizioni delle palline adiacenti.
- Chiedete agli studenti quale ipotesi si sta facendo quando si assume che la velocità orizzontale di un proiettile è costante. La risposta dovrebbe essere che la resistenza dell’aria è trascurabile.
Esperienza 2
In questa esperienza si mostrerà che la velocità orizzontale sarà ancora costante per un proiettile con velocità verticale non nulla (cioè per un angolo di gittata non nullo) ma sarà più piccola di quella di un proiettile con traiettoria con velocità iniziale verticale nulla (come nell’esperienza 1).
- Disporre il righello in posizione non orizzontale. Suggeriamo un inclinazione abbastanza pendente, in modo da notare una apprezzabile differenza con l’esperienza 1.
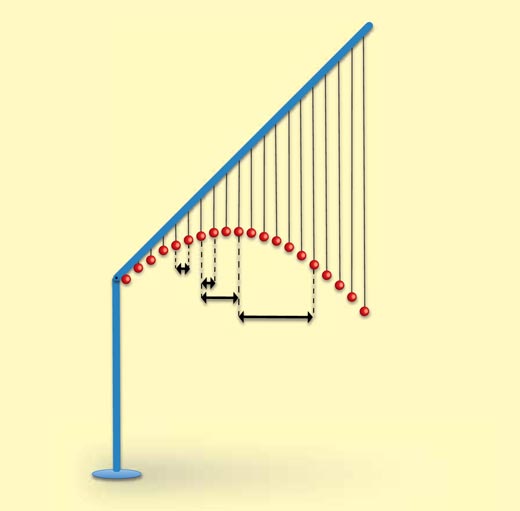
Immagine gentilmente concessa da Marlene Rau
- Usando il valore di t calcolato nell’esperienza 1 – o il valore di t usato per costruire il modello – chiedete agli studenti di calcolare la velocità orizzontale come nel punto 4 dell’esperienza 1.
Ancora una volta, se il modello è stato costruito accuratamente, gli studenti dovrebbero trovare che la distanza orizzontale percorsa in intervalli tempo uguali è costante, ma sarà naturalmente minore rispetto al caso in cui la velocità verticale è nulla (Esperienza 1) – le cordicelle di palline adiacenti saranno più vicine fra loro.
Esperienza 3
In questa esperienza gli studenti studieranno la distanza verticale percorsa in intervalli di tempo uguali per una traiettoria con velocità iniziale verticale nulla (come nell’esperienza 1). L’esperienza si presta meglio per gli studenti che non hanno partecipato alla costruzione del modello, sebbene può essere utile per consolidare la comprensione anche di quelli.
- Riportare il righello in posizione orizzontale.
Un cambiamento della velocità verticale è una accelerazione (a) e dall’equazione F = m a sappiamo che un’accelerazione è il risultato di una forza – in questo caso la gravità che agisce sull’oggetto. Dato che questa forza è costante dall’equazione del moto uniformemente accelerato, si ottiene
la distanza verticale percorsa (s) = (u t) + (½ a t2)
dove u = velocità iniziale.
Poiché la velocità verticale iniziale (u) è zero, (u t) può essere ignorato, e dato che ½ a è costante, l’espressione ci dice che la distanza verticale percorsa è proporzionale al quadrato del tempo. Si può far notare che l’accelerazione (a) e la gravità (g) sono intercambiabili in questo contesto perché entrambe rappresentano l’accelerazione dei caduta libera.
- Chiedete agli studenti di calcolare il tempo trascorso per ogni posizione delle palline (notare che i corrispondenza del perno t = 0) – i valori saranno 1t per la prima pallina, 2t per la seconda, ecc. (vedere Tabella 1), usando come valore di t quello del modello costruito.
- Fate misurare agli studenti le lunghezze delle cordicelle a differenti posizioni – se avete poco tempo a disposizione per farle misurare tutte scegliete le due codicelle estreme e 3 nel mezzo. Queste lunghezze sono le distanze di caduta per ciascuna posizione scelta.
- Fate disegnare un grafico della distanza verticale percorsa in funzione del tempo impiegato elevato al quadrato (cioè t2 per il punto1, (2t)2 per il punto 2, ecc.) per ciascuna delle posizioni misurate incluso lo zero.
Invece di usare il valore di t del modello, gli studenti potrebbero usare il valore calcolato nell’Esperienza 1. Se questo non corrisponde al valore del modello il grafico sarà ancora una retta mostrando la stessa correlazione ma solo dopo il secondo punto del grafico.
Esperienza 4
Questa semplice esperienza serve a rinforzare la comprensione del fatto che le componenti verticale e orizzontale della velocità sono indipendenti l’una dall’altra.
- Posizionare il righello a 45 gradi rispetto alla verticale.
- Gli studenti dovrebbero rendersi conto del fatto che gli spostamenti verticali non sono cambiati, cioè la distanza fra ciascuna pallina e il righello è sempre la stessa a prescindere dall’angolo di inclinazione del righello, poiché le lunghezze delle cordicelle non sono cambiate.
Altre idee
Qui abbiamo altre idee da proporre agli studenti sulle quali investigare:
- Per quale inclinazione del righello si ha la massima gittata? Cosa succede se si considera la superficie non piana?
- Come si può adattare il modello per pianeti in cui l’accelerazione di gravità è più piccola o più grande di quella terrestre (9.8 m/s2)?
- Gli studenti riescono a determinare la velocità verticale istantanea prendendo coppie di letture dal righello ad angolo fissato? Riescono a usare queste velocità per verificare quanto il modello si avvicina a predire una accelerazione di 9.8 m/s2?
- Cambia la determinazione dell’accelerazione verticale alla posizione angolare a cui è fissato il righello?
Resources
- Freier GD, Anderson FG (1981) Demonstration Handbook for Physics (2nd edition). College Park, MD, USA: American Association of Physics Teachers. ISBN: 9780917853326
- Per vedere una animazione del moto di un proiettile, andare su: www.phy.hk/wiki/englishhtm/ThrowABall.htm
- Su Wikipedia c’è una chiara spiegazione della traiettoria di un proiettile, in particolare nella sezione ‘Angle θ required to hit coordinate (x,y)’: http://en.wikipedia.org/wiki/Trajectory_of_a_projectile
Review
L’idea che c’è dietro l’esperimento della costruzione del modello proposto in questo articolo è molto creativa, e gli studenti impareranno attraverso una partecipazione attiva, utilizzando diverse capacità nella sua realizzazione. Una volta costruito il modello servirà anche come un aiuto visuale per la teoria in classe; ciò viene completato con proposte per un insieme di attività che può essere effettuata durante le lezioni.
A seconda delle abilità degli studenti, i docenti possono scegliere di lasciare la scoperta della teoria che c’è dietro gli esperimenti ai loro studenti, o altrimenti guidarli alla soluzione.
Questa attività dovrebbe inserirsi sicuramente nel curricolo della fisica come parte dell’insegnamento della cinematica (moto dei proiettili) argomento incluso nella maggior parte dei programmi europei. L’attività può considerarsi come interdisciplinare poiché la costruzione del modello richiede capacità nell’ambito del disegno e della tecnologia. C’è anche naturalmente la componente matematica.
Jürgen Azzopardi, Malta





