Misure intelligenti dei cieli Teach article

Tradotto da Rocco G. Maltese. Insegnare ai propri studenti come usare gli smartphones per alcuni calcoli astronomici alla portata di mano.

Esattamente sapete dove vi trovate in questo momento? Un modo per saperlo potrebbe essere quello di utilizzare la funzione di posizionamento satellitare (spesso detta GPS) del vostro cellulare. In passato, avreste potuto interrogare le stelle per sapere dove vi trovavate – specialmente se eravate un marinaio in mezzo al mare senza alcun punto di riferimento lungo la costa.

In questo articolo, descriviamo alcuni degli sviluppi storici della navigazione che si affidavano alle stelle, e dimostriamo come queste tecniche tradizionali possano essere riprodotti in classe usando delle semplici applicazioni di un telefono cellulare. I vostri studenti possono utilizzare la funzione GPS dei loro cellulari per verificare la precisione dei loro lavori prima di considerare delle potenziali sorgenti di errori.

Adatte per studenti di età compresa tra i 14-18 anni, le due attività riguardano la storia, l’astronomia, la geografia e la matematica: Determinare la vostra latitudine (figura 1) con il Sole, e determinare la propria latitudine con la stella Polare. I dettagli di una attività collaborativa tra scuole, per calcolare la circonferenza della Terra, posso essere tratti dal sito internet di Science in School. Le tre attività richiedono poco più di un telefonino e si possono eseguire in meno di un’ora.

Determinare la latitudine utilizzando l’altezza del Sole

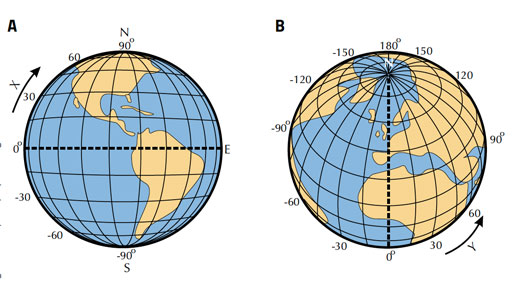
“Cosa significa mezzogiorno?” potrebbe sembrare una strana domanda. Certamente per mezzogiorno intendiamo le ore 12 in punto? Precisamente, il mezzogiorno solare è l’stante in cui il Sole attraversa il meridiano, o la linea di longitudine, e culmina a nord o a sud. Questo succede quando il Sole si trova nel punto più alto nella volta celeste e le ombre sono le più corte di tutta la giornata. Questo è il momento in cui la posizione del Sole può essere utilizzata per determinare la vostra latitudine, detta anche distanza angolare dall’equatore.

Come si fà? Consideriamo di trovarci in uno dei due Equinozi (approssimativamente il 20 Marzo e il 23 Settembre di ogni anno), quando il piano dell’Equatore passa per il centro del Sole (figura 2).

• A: Immagina di stare sull’equatore, alla latitudine 0°, a mezzogiorno: il Sole è proprio al di sopra della tua testa. Se misuri l’altezza del Sole (cioè l’angolo dell’elevazione al di sopra dell’orizzonte) dovresti trovare che è 90° (figura 3A). Sottraendo questo numero da 90° troviamo 0°, cioè la latitudine.

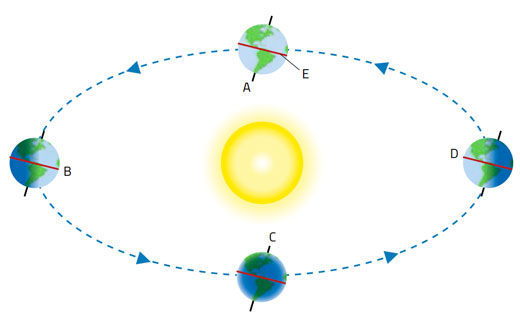
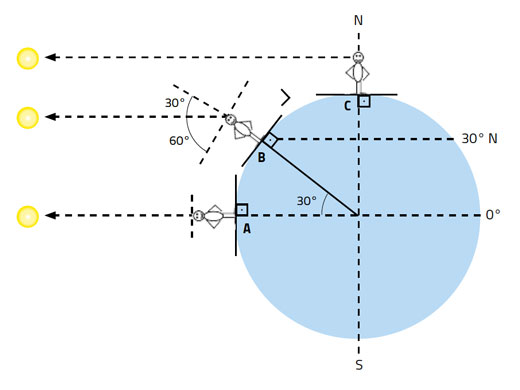
(Abbiamo stabilito che il Sole a a mezzogiorno è generalmente o verso Nord o verso Sud. Agli equinozi è direttamente al di sopra delle nostre teste.)

• B: Una vostra compagna si trova o al Polo Nord o al Polo Sud (rispettivamente, latitudine 90° N o 90° S). In quello stesso istante, lei dovrebbe osservare che il Sole si trova direttamente sull’orizzonte: con una altezza di 0° (figura 3B). Sottraendo a questo valore 90° otteniamo 90°, cioè la latitudine.
• C: Un altro compagno si trova sullo stesso tuo meridiano, ma alla latitudine di 30° N. Poiché si trova sullo stesso tuo meridiano, anche per lui è mezzogiorno, ma dovrebbe osservare il Sole ad una altezza di di 60° sull’orizzonte (figura 3C). Sottraendo questo valore da 90° otteniamo 30°: cioè la sua latitudine.

Latitudine = 90° – altezza del Sole a mezzogiorno all’equinozio               (Equazione 1)

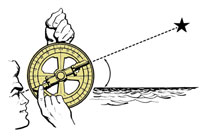
Come possiamo praticamente utilizzare queste conoscenze? Nel 15mo e ai primi anni del 16mo secolo, molti navigatori utilizzavano l’astrolabio per misurare l’altezza del Sole e calcolare così la latitudine della loro imbarcazione. L’astrolabio marinaresco era essenzialmente un inclinometro: sospeso sul piano orizzontale, si può traguardare un corpo celeste, ad esempio il Sole. Si può un’alidada rotante per leggere l’altezza del corpo celeste sulla scala riportata sul scala graduata riportata sul cerchio più esterno  dell’alidada (figura 4).

Poiché un astrolabio marino è uno strumento piuttosto semplice da costruire^w2, è altrettanto semplice utilizzare uno smartphone per misurare l’altezza del Sole con l’aiuto dell’applicazione dell’inclinometro. Prima di affrontare questo metodo, tuttavia, abbiamo bisogno di introdurre alcune ulteriori formule affinché si possano utilizzare per tutto l’arco dell’anno.

A causa della inclinazione dell’asse di rotazione della Terra (23.45°; 23°27’) e per il fatto che la terra orbita attorno al Sole, è solo agli equinozi che esso appare al di sopra dell’equatore. A iniziare con l’equinozio di Marzo, la posizione del Sole a mezzogiorno sembra che si muova a nord dell’equatore, raggiungendo la sua altezza massima di 23.45° al solstizio di Giugno, ritornando a 0° all’equinozio di Settembre, muovendosi poi a sud dell’equatore per raggiungere -23.45° al solstizio di Dicembre. Questo angolo definisce la declinazione del Sole (figura 5).

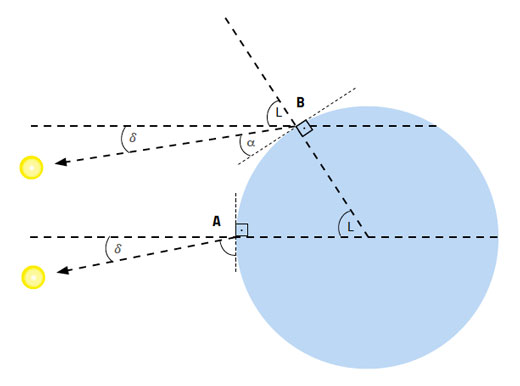
Così l’altezza del Sole a mezzogiorno, che i primi navigatori misuravano con un astrolabio marino e che noi oggi possiamo misurare con uno smartphone, dipende sia dal periodo dell’anno – e perciò dalla declinazione del Sole – e dalla nostra latitudine (figura 6):

Altezza del Sole a mezzogiorno = 90° + declinazione – latitudine               (Equazione 2)

o, meglio:

Latitudine            = 90° – altezza del Sole a mezzogiorno + declinazione               (Equazione 3)

Per determinare la declinazione del Sole i primi naviganti utilizzavano le tavole dei dati astronomici o un più sofisticato astrolabio astronomico che riportava su un altro cerchio rotante, la declinazione del Sole. Possiamo ottenere la stessa informazione da una applicazione dello smartphone chiamata planetarium, dopo di ciò saremo in grado di l’altezza del Sole e quindi la nostra latitudine.

Materiali

Ogni gruppo di studenti avrà bisogno di:

• Smartphone con installate l’app dell’inclinometro e dell’astrolabio
• Una cannuccia per bevande
• Nastro adesivo
• Una livella ad alcool (facoltativo)

Procedura

Per determinare la latitudine, i vostri studenti avranno bisogno di:

1. Nastro adesivo per fissare la cannuccia allo smartphone lungo uno dei suoi lati (figura 7). Questa rappresenterà l’alidada.
2. Utilizzare l’app dell’astrolabio per determinare l’istante del mezzogiorno locale, e la declinazione del Sole.

Dipendendo dalla vostra posizione all’interno del fuso orario, il mezzogiorno locale cadere alle 11.30, e se vi è l’ora legale, il mezzogiorno può cadere anche alle 13.30 (1.30 pm).

3. Posizionando lo smartphone con la cannuccia sul lato superiore, puntare la cannuccia in direzione del Sole. Quando l’ombra della cannuccia raggiunge il minimo, lo smartphone sarà correttamente allineato (figura 7).
4. Utilizzando l’applicazione dell’inclinometro, leggere l’angolo di elevazione del Sole.
5. Utilizzare l’equazione 2 per stimare la latitudine.

In alternativa a questo metodo per aiutare gli studenti ad allineare più precisamente il loro smartphone in direzione del Sole e misurare la sua altezza potrebbero costruire un treppiede dove appoggiare lo smartphone. I dettagli di questa procedura e i materiali necessari si possono acquisire online^w3.

Discussione

Domandate ai vostri studenti di confrontare i risultati ottenuti con quelli registrati dalla funzione GPS dello smartphone o utilizzando l’applicazione del planetario. Quanto saranno precisi i loro calcoli? Quali fonti di errore potrebbero aver influenzato la misura?

Naturalmente l’accuratezza dipende dalla precisione con la quale gli studenti hanno eseguito il loro lavoro, per es., quanto è stato preciso l’allineamento della cannuccia posizionata sul bordo dello smartphone, o quanto l’ombra generata dai raggi solari era veramente al suo minimo. Per la massima accuratezza, le misure dovrebbe essere prese a mezzogiorno, ma alcuni minuti prima o dopo non dovrebbero influire sulla stima poiché a mezzogiorno il Sole si trova alla sua massima altezza, ed essa varia molto lentamente.

Gli smartphone sono in grado di misurare gli angoli con una precisione di 0.1°, il che non è male. Potrebbe essere interessante, comunque, calibrare l’app dell’inclinometro con una livella ad alcool verificando se la lettura è perfettamente orizzontale.

Potreste altresì chiedere ai vostri alunni perché sebbene la latitudine si è potuta misurare sin dai primordi della navigazione, è solo nel 18.mo secolo che è stato possibile misurare la longitudine.

La risposta risiede nella rotazione della Terra: 360° in un giorno o circa 15° in un ora. Così confrontando il tempo locale con il tempo del punto di riferimento di longitudine nota, è possibile determinare la propria longitudine. L’ora locale può essere stimata con il Sole, ma la difficoltà risiedeva nella determinazione dell’ora del punto di riferimento: un orologio molto preciso, anche su una nave in navigazione, così solo nel 1759 John Harrison inventò un tale cronometro marino.

Determinare la latitudine utilizzando l’altezza della Polare

Nella precedente attività, abbiamo misurato l’altezza del Sole a mezzogiorno locale: cioè nel momento in cui il Sole passa sul meridiano dell’osservatore. In questo – e solo in questo momento – che il Sole apparirà culminare a sud o verso nord. Se i vostri studenti hanno calcolato la latitudine con il Sole, in altri momenti della giornata, i loro risultati sarebbe risultati errati. Fortunatamente, vi è un altro metodo che non è così sensibile coi tempi – sebbene funzioni solo nell’emisfero settentrionale bisogna che sia buio – ed è correlato alla Polare, cioè la stella del Nord.

Mentre la posizione delle altre stelle sembra variare al trascorrere del tempo durante la notte, la Polare appare fissa verso nord (figura 8), poiché la sua posizione è in direzione dell’asse di rotazione terrestre. Se vi trovaste al Polo Nord (latitudine 90° N), la stella Polare vi dovrebbe apparire direttamente sopra di voi, con un’altezza di 90°. All’equatore (latitudine 0°), invece, la Polare vi dovrebbe apparire all’orizzonte, con una altezza di 0°. Così, l’altezza della Polare è uguale alla vostra latitudine: se vi trovaste a Parigi, alla latitudine di 49° N, dovreste misurare l’altezza della Polare di circa 49°.

Latitudine = altezza della Polare               (Equazione 4)

I primi navigatori usano un astrolabio marino per navigare con le stelle, con lo stesso metodo che adoperavano con il Sole. Nuovamente possiamo usare uno smartphone.

Materiali

• Smartphone con installate le app di un inclinometro e di un planetario
• Binocolo (facoltativo)
• Torcia (facoltativa)

Procedura

E’ più semplice calcolare la vostra latitudine con la Polare che con il Sole: non è necessario conoscere la declinazione, perché la posizione della Polare rimane invariata durante tutto l’anno.

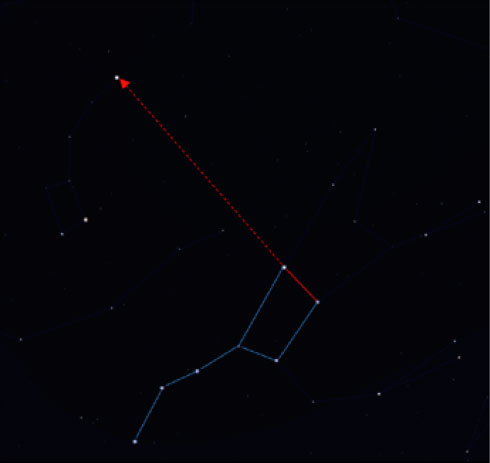
Come si individua la Polare? Cercate la costellazione dell’Ursa Major (Orsa Maggiore), (Big Dipper o Plough) (figura 9). Prolungare una retta ideale che congiunge le ultime due stelle del tetragono, per una lunghezza pari a sette volte la loro distanza. La prima stella brillante che si incontra lungo questa retta è la stella Polare, che fa parte della costellazione dell’Ursa Minor (Orsa Minore),  (Little Dipper), si può utilizzare alternativamente anche l’app del planetario e la funzione di ricerca della stella Polare.

Poiché la luce della Polare è molto più debole del Sole, le  osservazioni della Polare possono essere effettuate direttamente, senza un alidada, ma questa sua debolezza la rende anche piuttosto difficile da individuare. Si può far pratica con oggetti celesti più luminosi come i pianeti o la Luna.

Domandate ai vostri studenti di:

1. Tenere lo smartphone con il lato più lungo verso l’alto che punti direttamente alla Polare, guardare la superficie del cellulare.

Avranno bisogno di una luce portatile per fare ciò, per riconoscere lo spigolo del cellulare al buio.

2. Utilizzare l’app dell’inclinometro, leggere l’angolo di elevazione della Polare. Questa lettura vi fornirà una stima della vostra latitudine.

In alternativa a ciò, lavorando in coppia, si possono usare i binocoli. Uno studente dovrebbe puntare il binocolo verso la Polare, in modo tale che la stella rimanga al centro del campo visivo (appoggiando il binocolo su un muretto in modo che rimanga ben fermo). Un altro studente dovrebbe appoggiare il cellulare sul binocolo e determinare così l’angolo dell’elevazione della Polare utilizzando la app dell’inclinometro. Se è necessario calibrate il binocolo, posatelo su una superficie orizzontale, e ponetevi sopra il cellulare e verificate l’angolo con l’app dell’inclinometro.

Discussione

Domandate ai vostri studenti di determinare l’altezza della Polare utilizzando l’app del planetario. Quanto è stata precisa la loro osservazione? Quanto si discosta la stima della latitudine rispetto a quella fornita dal planetario o dal GPS del loro smartphone? Quali fonti si errore pensano che vi siano state, diverse da quelle della precedente attività?

Sebbene la Polare sia una stella luminosa, è considerevolmente più debole del Sole, il che potrebbe rendere più difficile una lettura accurata della latitudine.

Un’altra fonte di errore è la posizione della Polare. Noi affermiamo che la Polare dovrebbe apparire al di sopra della vostra testa se vi trovaste al Polo Nord: con una altezza di 90°. Di fatto la sua altezza al Polo è di 89.3°, il che introduce un errore di 0.7° nei calcoli dei vostri studenti, che corrisponde ad una differenza di posizione di circa 100 km.

Questo metodo funziona abbastanza bene alle medie latitudini. Molto più a Nord, è difficile osservare la Polare che rimane al di sopra delle vostre teste. Vicino all’equatore, la Polare appare vicino all’orizzonte, il che significa che vi saranno dei disturbi introdotti dalla luminosità dell’atmosfera.

Riconoscimenti

Questo articolo si basa sull’attività pubblicata da Science on Stage, la rete Europea per gli insegnanti di scienze, tecnologia, ingegneria e matematica (STEM), che inizialmente fu inaugurata nel 1999 dal forum EIROforum, l’editore di Science in School. Science on Stage mette insieme gli insegnanti di scienze di tutta Europa per uno scambio di idee di insegnamento e le migliori esercitazioni con colleghi entusiasti provenienti da 25 paesi.

Alla riunione di Science on Stage di Vienna, Austria, e Berlino Germania, oltre alle discussioni attraverso email e la piattaforma educativa pubblica di Moodle, 20 insegnanti provenienti da 14 paesi Europei hanno lavorato insieme per sviluppare 11 unità didattiche che sfruttano le proprietà degli smartphone e delle applicazioni per costruire lezioni di matematica, fisica, chimica o biologia. Queste unità didattiche sono state pubblicate nel 2014 da Science on Stage Germania con il titolo iStage 2: Smartphones in Science Teaching (lo smartphone nell’Insegnamento delle Scienze)^w4. Il progetto è stato finanziato da SAP.

Oltre a Gerhard Rath e Philippe Jeanjacquot, Pere Compte dalla Spagna e Immacolata Ercolino dall’Italia sono stati coinvolti nello sviluppo di questo progetto. Martin Pratl ha fonito un valido aiuto con il testo dell’articolo.