Supporting materials
Download
Download this article as a PDF

Übersetzt von Inci Aydin. Das Erforschen der Sehschärfe erfordert nicht nur biologische Experimente, sondern auch ein gewisses Verständnis der zugrundeliegenden Physik.
Die Sehschärfe ist ein Maß dafür, wie stark unser Sehvermögen ist, insbesondere wie gut wir kleine Details auflösen können. Optiker beurteilen dies, indem sie uns bitten, von einer Schautafel zu lesen bis die Buchstaben uns zu klein werden, um sie klar zu erkennen.
Eines der biologischen Faktoren, die die Sehschärfe bestimmen, ist die Dichte der Fotorezeptorzellen in der Netzhaut (Retina) (siehe Kasten, “Wie unsere Augen funktionieren”). Dies veranlasst die faszinierende Frage: Könnte eine größere Dichte von Rezeptoren in der Retina unsere Sehkraft verbessern? Um diese Frage zu beantworten, müssen wir die Biologie des visuellen Systems und die Physik des Lichts beachten. Diese Themen sind meist Teil der Biologie- und Physiklehrpläne der Sekundarschule. Jedoch werden sie traditionellerweise separat und oft unterschiedlichen Gruppen von Schülern gelehrt. Dagegen wird die hier vorgeschlagene lehrplanübergreifende Vorgehensweise den Schülern ermöglichen, ein tiefes Verständnis sowohl der Biologie als auch der Physik der Sehschärfe zu erlangen, und sie wird eine allgemein gültige Nachricht vermitteln: Viele Probleme in der modernen Wissenschaft können am besten durch Teamarbeit und interdisziplinäre Kollaboration gelöst werden.
Dieser Artikel beschreibt einen einfachen Weg zur Bewertung der Sehschärfe, indem eine Schautafel erstellt und zur Berechnung der Auflösung des Auges benutzt wird. Diese Methode kann verwendet werden, um den kleinsten Abstand auf der Retina abzuschätzen, bei dem die Bilder von zwei Punkten als zwei deutlich getrennte Objekte identifiziert werden können. Ein Nachfolgeexperiment, das in den zusätzlichen Materialien zur Verfügung steht, bringt basierend auf den physikalischen Eigenschaften von Licht diesen Abstand in Zusammenhang mit den theoretischen Grenzen der Sehschärfe.
Die beiden Übungen sind am besten für Schüler im Alter von 16-19 Jahren geeignet und dauern jeweils etwa 2 Stunden, inklusive der Vorbereitung und Datenanalyse. Zwei weitere Stunden sollten für die Diskussion der Ergebnisse vorgesehen werden.
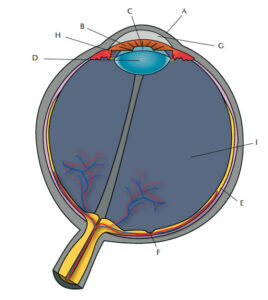
Von Objekten reflektierte Lichtstrahlen treten durch die Pupille in das Auge. Vier Bestandteile des Auges – Hornhaut, Linse, wässrige Flüssigkeit und glasige Flüssigkeit – fokussieren die Lichtstrahlen auf der Retina, der Innenseite des Augapfels (Abbildung 1). Die Retina ist in unterschiedlichen Schichten aufgebaut, die jeweils Millionen lichtsensitive Fotorezeptoren enthalten, welche wiederum Signale über andere Zellen, z.B. die retinalen Ganglienzellen, zum Gehirn übertragen. Die Fotorezeptorzellen sind spezialisierte Nervenzellen, von denen es zwei Typen gibt – Stäbchen und Zapfen (nach ihrer Form benannt). Zapfen befinden sich hauptsächlich im Zentrum der Netzhaut und ermöglichen scharfes Farbsehen in hellem Licht. Stäbchen, die sich am Rand der Retina befinden, helfen uns, Bewegung zu erkennen und bei gedämmtem Licht zu sehen, und ermöglichen periphere Sicht. Die Dichte der Fotorezeptoren (sie kann größer als 200 000 Zellen pro Quadratmillimeter in der Fovea Centralis sein) in der Retina spielt eine wichtige Rolle für die Sehschärfe.
Die Winkelauflösung des menschlichen Auges ist ein Maß des kleinsten Winkels zwischen zwei Punkten, die als deutlich getrennt wahrgenommen werden, und steht teilweise in Beziehung mit der Dichte der Fotorezeptoren in der Netzhaut. Sie ist normalerweise etwa 1 Bogenminute (1/60 eines Grads). In dieser Übung wird die Winkelauflösung berechnet, indem das Verhältnis vom Abstand zwischen zwei Punkten zum Abstand zwischen dem Beobachter und den Punkten bestimmt wird. Dieses vereinfachte mathematische Vorgehen (welches die viel kompliziertere Berechnung der Tangente des Winkels α in Abbildung 2 ersetzt) ist möglich, weil die Winkelauflösung von sehr kleinen Werten ausgeht. In der Mathematik ist diese Abkürzung als die Kleinwinkelnäherung bekannt. Wie in Abbildung gezeigt, kann das errechnete Verhältnis dann genutzt werden, um den Abstand zwischen diesen zwei Punkten, projiziert auf die Netzhaut, zu schätzen.
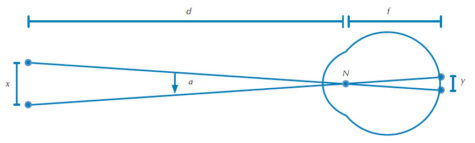
d = Abstand zwischen dem Objekt (in diesem Experiment, die Schautafel ) und dem Auge der Versuchsperson; f = Brennweite des reduzierten Auges; x = die kleinste wahrgenommene Lücke zwischen zwei Punkten (in diesem Experiment, die Breite der kleinsten wahrgenommenen Lücke, die die zwei schwarzen Balken in einem unterbrochenen Balkenmuster trennt); y = Abstand zwischen den Bildern dieser zwei Punkte auf der Netzhaut; N = virtueller Brennpunkt.
Mit freundlicher Genehmigung von Günther KH Zupanc
Die Schüler werden ein Schaubild mit einfachen, schwarzen Linien, die durch Lücken mit unterschiedlicher Weite getrennt sind, erstellen. Sie werden dann gebeten, anzugeben, welche Linien sie als getrennt wahrnehmen und welche als verschmolzen erscheinen. Diese Ergebnisse werden sie nutzen, um eine Schätzung der Winkelauflösung, und daher den Abstand zwischen den Rezeptoren im Auge, zu berechnen.

Die Winkelauflösung des menschlichen Auges schwankt typischerweise zwischen 40 Bogensekunden und 1 Bogenminute. Um zwei einzelne Punkte wahrzunehmen, sind mindestens drei aneinandergereihte Fotorezeptoren erforderlich: einen, um das Licht von jedem der Punkte zu empfangen, und einen für die Lücke zwischen den Punkten. Für eine Winkelauflösung von 1 Bogenminute (das entspricht 0.3 m auf einer Entfernung von 1 km) sind die Bilder auf der Retina durch etwa 6 µm getrennt, was bedeutet, dass der Mitte zu Mitte Abstand zwischen zwei benachbarten Rezeptoren 3 µm beträgt. Bei einer Winkelauflösung von 40 Bogensekunden beträgt der Abstand zwischen den Bildern der Punkte ungefähr 4 µm.
Die tatsächliche Auflösung des Auges wird nicht nur durch den Abstand zwischen den Fotorezeptoren beeinflusst, sondern auch durch die Beugung des Lichtes, wenn es durch die Pupille dringt. Sie können dies weiter erkunden, indem Sie Experiment 2 herunterladen.
Könnte also die Sehschärfe verbessert werden, indem die Dichte der Zapfen in der Netzhaut erhöht wird?
Eine Winkelauflösung von 40 Bogensekunden wird nur erreicht, wenn wir starr auf einen Gegenstand schauen. Das Bild des Gegenstandes wird dann auf einen bestimmten Teil im Zentrum der Retina, der Fovea Centralis, projiziert, der nur Zapfenfotorezeptoren enthält. Die Dichte der Zapfen in der Fovea ist viel größer als irgendwo sonst in der Retina, und die Zapfen hier haben einen Durchmesser von nur 3 µm (verglichen mit bis zu 10 µm in anderen Bereichen der Retina). Unter Berücksichtigung von ein wenig extrazellulärem Raum um jeden Zapfen herum (z.B. für den Transport von Nährstoffen) beträgt der Mitte zu Mitte Abstand zwischen den Zapfen in der Fovea etwa 4 µm. Daher ist die Dichte der Zapfen in der Retina schon sehr nahe an der maximal möglichen Packungsdichte.
Wie man in dem Nachfolgeexperiment erkunden kann, bedeutet Lichtbeugung im Auge, dass der kleinste auflösbare Abstand zwischen zwei Lichtpunkten etwa 5 µm beträgt, was einen vorhergesagten minimalen Abstand von ungefähr 2.5 µm zwischen Zapfen ergibt. Unter Berücksichtigung von etwas extrazellulärem Raum zwischen den Zapfen, stimmt dieser theoretisch vorhergesagte Abstand exzellent mit dem tatsächlichen Abstand von etwa 4 µm zwischen den Zapfenrezeptoren in der Fovea Centralis überein. Deshalb wäre eine weitere Erhöhung der Zapfendichte aus biologischen Gründen nicht möglich, und würde basierend auf den physikalischen Grenzen, die durch die Eigenschaften des Lichts bestimmt werden, zu keiner signifikanten Steigerung der Sehschärfe führen.
Dieser Artikel beschreibt zwei Experimente im Zusammenhang mit der Sehschärfe, ein Beispiel für die zahlreichen in der Natur vorfindlichen Verbindungen zwischen Biologie und Physik. Lehrplanübergreifende Übungen können die Wissenschaft reizvoller machen und eine große Gelegenheit bieten, mit anderen Lehrern zusammenzuarbeiten.
All die für die Experimente erforderlichen Materialien sind einfach zu bekommen und die Anweisungen sind leicht zu verfolgen. Daher ist es für die Schüler angemessen, die Übungen in kleinen Gruppen durchzuführen.
Der Text könnte als Grundlage für Diskussionen über die Wichtigkeit von Gruppenarbeit und interdisziplinärer Zusammenarbeit zur Lösung vieler Probleme in der modernen Wissenschaft und auch in anderen Fächern dienen.
Mireia Güell, Spanien
Download this article as a PDF