Uczniów można zachęcić i zaangażować do modelowania zmian klimatu Teach article
Tłumaczenie: Anna Malańska i Bogusław Malański. Cóż stoi na przeszkodzie by zaangażować uczniów w przewidywanie zmian klimatycznych? Pomogą w tym Dudley Shallcross i Tim Harrison w Uniwersytetu w Bristol, Wielka Brytania?
Zmiana klimatu i globalne ocieplenie są tematami „na czasie”. Niewątpliwie zasługują na uwagę w realizacji programu szkolnego. But how do we predict how our climate is going to change? Jak można przewidzieć rozwój zmian klimatycznych na Ziemi? Wydaje się, że właściwym sposobem jest zapoznać uczniów z elementarnym modelowaniem klimatu. W artykule tym pokazujemy jak uczniowie mogą użyć prosty arkusz kalkulacyjny w celu zbadania, jak poszczególne czynniki wpływają na klimat na Ziemi? (tłum. znajomość elementarnej matematyki, przekształceń, podstawy fizyki, jak i posługiwania się arkuszem kalkulacyjnym np. Excelem są nieodzowne).
Pierwsza próba modelowania klimatu
Najprostszym modelem klimatycznym jest model opisujący równowagę między energią dostarczaną przez Słońce, a energią rozpraszaną przez Ziemię w przestrzeń pozaziemską. W skrócie: „energia otrzymana = energia rozpraszana”. W artykule tym pod słowem “energia” będziemy rozumieli natężenie przepływu energii tzn. ilość przepływającej energii w ciągu sekundy. Z pomiarów wiadomo, że energia dochodząca od Słońca do górnych warstw atmosfery (w ciągi 1 sekundy) wynosi: 1370 Wm-2– wielkość ta; S – nosi nazwę stałej słonecznej.
Rozpoczniemy obliczenia od oszacowania średniej temperatury powierzchni Ziemi -TE. Zakładamy, że Ziemia ma kształt idealnej sfery o promieniu RE. W tym uproszczonym modelu widać, że Ziemia absorbuje energię na powierzchni πRE2 (płaski dysk atmosfery), a emituje energię z powierzchni 4πRE2(całkowita powierzchnia kulista).
(a) energia na wejściu = energia na wyjściu
i stosując prawo Stefana-Boltzmanna (ramka)
(b) Energia na jednostkę powierzchni w jednostce czasu x powierzchnia całkowita(okrąg) = energia na jednostkę powierzchni w jednostce czasu x powierzchnia całkowita(kula)
(c) 1370 x πRE2 = σTE4 x 4πRE2
Prosta manipulacja równaniem daje:
σTE4 = 1370 = S/4
4
TE4 = 1370
(4 x 5.67 x 10-8)
TE = 279 K (6 °C)
Gdzie s jest stałą Stefan-Boltzmann’a równą (5.67 x 10-8 Wm-2K-4).
Na pierwszy rzut oka, ten uproszczony model wygląda rozsądnie, chociaż, jak wiadomo średnia temperatura powierzchni Ziemi wynosi 16 °C. (rozpatrzeć to zagadnienie można dokładniej, Np. rozpatrując różne strefy klimatyczne). Problem z tym uproszczonym leży gdzie indziej. Nie cała energia słoneczna jest pochłaniana, albowiem pewna jej część jest natychmiast odbijana przez chmury oraz obszary pokryte lodem i wysyłana z powrotem w przestrzeń.
W przybliżeniu około 24% padającej energii jest odbijana z powrotem przez chmury i około 6% przez obszary pokryte lodem. Zjawisko to nosi nazwę albedo (oznaczane literą -A). Dla Ziemi albedo wynosi 30% (lub 0.3). Z tego powodu lewą stronę równania (c) należy zmienić, jak następuje 0.7 x πRE2. Odpowiednio policzona średnia temperatura powierzchni Ziemi wyniesie:
TE4 = 1370 x 0.7
(4 x 5.67 x 10-8)
TE = 255 K (-18 °C)
Ta wartość jest zdecydowanie za mała. Prowadzi to do pytania; „dlaczego zatem Ziemia jest tak ciepła?” Aby odpowiedzieć na to pytanie należy wprowadzić model nieco bardziej złożony.
Konieczne podstawy teoretyczne z fizyki
Ciało doskonale czarne i prawo Stefana_Boltzmanna’a
Wszystkie ciała emitują energię postaci fali elektromagnetycznej. Ciało doskonale czarne jednocześnie absorbuje energię z całego zakresu promieniowania elektromagnetycznego. Ciało to emituje energię i wielkość tej emisji jest funkcją temperatury powierzchni.
Prawo Stfana-Boltzmann’a opisuje całkowitą energię (I) promieniowania, jakie emituje ciało doskonale czarne w danej temperaturze T. Stosowne równanie jest proste:
I(T) = σT4 (Równanie 1)
gdzie:
I – jest energią emitowaną przez jednostkę powierzchni w czasie 1 sekundy (Wm-2)
T – jest temperaturą bezwzględną
σ jest stałą Stefan-Boltzmann’a równą (5.67 x 10-8 Wm-2K-4).
Model z jedną warstwą atmosfery otaczającej Ziemię
Jeżeli założymy, że atmosfera zbudowana jest tylko z jednej warstwy gazów mieszalnych, to możemy zbudować bardziej precyzyjny model. Warto w tym celu użyć arkusza kalkulacyjnego (tłum. na przykład Excel). W modelu tym można zmieniać absorpcję przez atmosferę światła widzialnego docierającego ze Słońca oraz absorpcję promieniowania podczerwonego emitowanego z Ziemi.
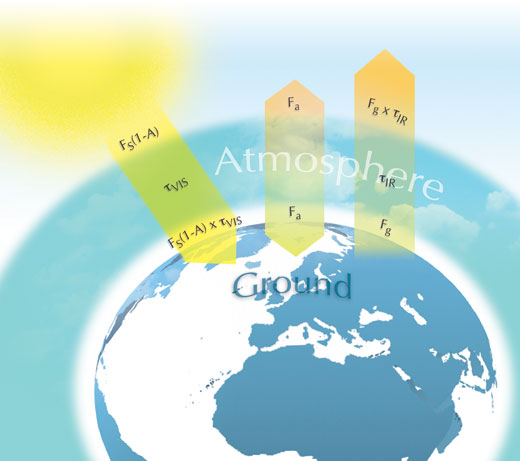
Poniższy rysunek pokazuje wszystkie czynniki tego modelu. FS jest stałą słoneczną podzieloną przez 4 (S/4), co wynika z różnicy energii dostarczanej do płaszczyzny dysku Ziemi, πr2a emitowanej przez jej całą powierzchnię, 4πr2 (założenie opisane w pierwszym, uproszczonym modelu). Energia dochodząca ze Słońca wynosi, zatem: FS(1-A)gdzie A- oznacza albedo, czyli część energii odbijanej z powrotem w przestrzeń. Energia dostarczana leży w zakresie UV oraz widzialnym. τVIS – oznacza część otrzymywanej energii, która nie jest pochłaniana przez atmosferę. Jeżeli atmosfera pochłania wszystko, to τVIS = 0, jeżeli atmosfera nic nie pochłania (całą energia dochodzi do powierzchni Ziemi), to τVIS = 1. Zatem ilość energii dochodzącej do powierzchni Ziemi wynosi: FS(1-A) x τVIS.
Ziemia zachowuje się w przybliżeniu, jak ciało doskonale czarne (tłum. dla niezorientowanych; takie ciało nie musi wyglądać „czarne”, ono ma się zachowywać według definicji, jak ciało doskonale czarne – patrz początek paragrafu: „Ciało doskonale czarne i prawo Stefana_Boltzmanna’a” lub dowolny podręcznik fizyki). Maksimum promieniowania Ziemi przypada w zakresie podczerwonym widma promieniowania. Niektóre gazy w atmosferze pochłaniają to promieniowanie (gazy cieplarniane). Podobnie, jak oznaczenie τVIS, τIR – oznacza część promieniowania podczerwonego, która nie jest pochłaniane przez gazy atmosfery. Zatem energia wypromieniowana przez Ziemię wynosi: Fg x τIR.
Oznaczając: Fa – energia pochłonięta przez atmosferę oraz balansując przepływ energii na powierzchni Ziemi i w atmosferze otrzymamy:
na powierzchni Ziemi:
FS(1-A) x τVIS + Fa = Fg (Równanie 2)
na górze atmosfery:
Fg x τIR + Fa = FS(1-A) (Równanie 3)
Z równania 2 i 3 otrzymamy:
Fg = FS(1-A)(1 + τVIS)
(1 + τIR)
Ostatecznie:
Fg = σTE4 = FS(1-A)(1 + τVIS)
(1 + tIR)
TE = [ FS(1-A)(1 + τVIS) ]0.25
[ σ(1 + τIR) ] (Równanie 4)
Jeżeli przyjmiemy następujące wartości:
FS = 1370/4 = 342.5 Wm-2 (stała słoneczna podzielona przez 4)
A = 0.3
τVIS = 0.8
τIR = 0.1
Równanie 4 daje nam wynik:
TE = 288.5 K (15.5 °C),
Co się bardzo dobrze zgadza z aktualną średnią temperaturą powierzchni Ziemi.
Równanie 4 można wprowadzić do programu Excel -Microsoft. Uczniowie zmieniając wartości parametrów mogą badać wpływ poszczególnych czynników na średnią temperaturę powierzchni Ziemi. Przykładowy wpływ poszczególnych czynników został przebadany i można go znaleźć na stronie Bristol Universityw1.
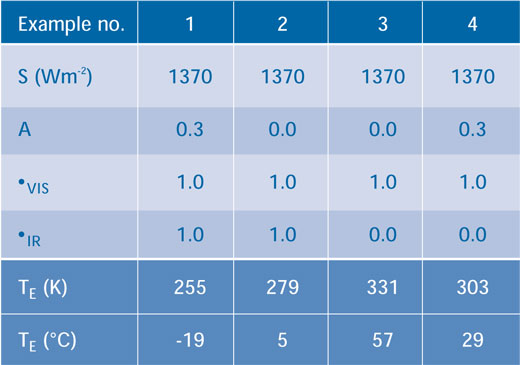
Tabela 1 pokazuje wpływ parametrów A, τVIS oraz τIR . Przykład 1: jeżeli założymy, że atmosfera nie pochłania, zarówno energii dochodzącej ze Słońca, jak i emitowanej przez Ziemię (τVIS i τIR są równe 1) oraz albedo równe 0.3; otrzymamy wynik 255 K (-180oC). Przykład 2; jeżeli założymy brak chmur i obszarów pokrytych lodem (albedo A=0), to otrzymamy temperaturę powierzchni Ziemi równą 279 K (6oC), Ilustruje to silny wpływ albedo na temperaturę. Przykład 3: brak chmur i obszarów pokrytych lodem, ale atmosfera pochłania promieniowanie podczerwone (τIR = 0.0); wtedy powierzchnia Ziemi ogrzewa się do 331K (58oC), Jeżeli dołożymy w naszym modelu chmury i lód – Przykład 4; otrzymamy spadek temperatury do 303K (30oC)
Możliwe pytania
Typowe pytania, jakie mogą zadać uczniowie i wymagające od uczniów użycia modelu w celu uzyskania odpowiedzi są:
- Które parametry mają największy wpływ na średnią temperaturę powierzchni Ziemi?
- Jeżeli średnia odległość Ziemi od Słońca wzrosłaby o 1%, to stała słoneczna zmniejszyłaby się o czynnik 1.0201, czyli wynosiłaby 1343 Wm-2. Jaki miałoby to wpływ na temperaturę powierzchni Ziemi? Proszę założyć albedo A=0.3, τIR of 0.3 i τVIS of 0.6.
(Stała słoneczna skaluje się, jak odległość do kwadratu; przysuwając, zatem Ziemię o 10% bliżej Słońca otrzymamy S = 1370/(0.9)2 = 1691 Wm-2 a oddalając o 1% dostaniemy S = 1370/(1.01)2 = 1343 Wm-2)
Oczywiście można zadać wiele innych ciekawych pytań takich jak:
- Załóżmy, że piaski Sahary można zamienić w zwierciadło (piasek można łatwo stopić i zamienić w niezłe lustro)
- jak wielkie musiałoby być to zwierciadło z piasku by oziębić powierzchnię planety o 1 °C?
- jaka by to była część powierzchni Sahary?
Model bardziej zaawansowany
Jak można nasz model porównać z modelem bardziej zaawansowanym, używanym chociażby przez Centrum Hadley’a Biura Meterologicznego Wielkiej Brytanii (patrz zdjęcia poniżej)? W swej istocie modele te są do siebie bardzo podobne, z wyjątkiem, że model używany w Centrum Hadley’a rozważa atmosferę ziemską zbudowaną z wielu warstw. Warstwy te, o różnych właściwościach, są rozmieszczone w zależnościom wysokości, szerokości oraz długości geograficznej. Dla każdej warstwy osobno liczone są współczynniki, tak jak to było zrobione w naszym modelu z pojedynczą warstwą. Uwzględniane są albeda, gazy cieplarniane, zachmurzenie, obszary pokryte lodem. Jeszcze bardziej zaawansowany model używany w Instytucie Haydley’a, rozważa przepływ ciepła przez wody oceanów oraz zużycie dwutlenku węgla CO2 przez rośliny. Jeżeli nasz uproszczony model jest przez ucznia zrozumiały, to zrozumienie modelu zaawansowanego nie stanowi już problemu.
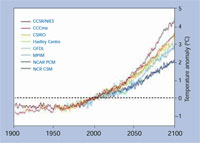
ocieplenia; Prognozowanie
globalnego ocieplenia na rok 2000.
Dane użyte w tym modelu zostały
wzięte z Międzynarodowego Panelu
– Centrum Dystrybucji Danych Zmian
Klimatycznych
Dzięki uprzejmości Robert A. Rohde;
Źródło ilustracji: Wikimedia Commons
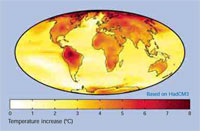
ocieplenia; lata 2070-2100, w
zestawieniu z prognozą na lata
1960-1990. Mapa prognozująca
globalne ocieplenie w wieku XXI.
Model przewiduje średni wzrost
temperatury powierzchni Ziemi o
3.00C – został zastosowany model
zmian klimatycznych
HadCM3 z centrum Hadley’a
Dzięki uprzejmości Robert A. Rohde;
Źródło ilustracji: Wikimedia Commons
Uczestnictwo w prawdziwej symulacji zmiany klimatu
Sieć Prognozowania Klimatuw2 jest największym eksperymentem starającym się przewidzieć zmiany klimatyczne w XXI wieku. Sieć ta korzysta z indywidualnych komputerów użytkowników z całego świata, którzy są w stanie udostępnić wolny czas pracy swoich maszyn – chociażby w czasie pracy komputera, gdy nie jest on wykorzystywany do granic swojej możliwości. Rozbudowany model klimatu zawiera wiele parametrów. Powoduje to wzrost ilości obliczeń. Nawet przy użyciu komputerów będących w dyspozycji Sieci Prognozowania Klimatu, takie obliczenia zajęłyby dużo czasu. Idea użycia indywidualnych komputerów podłączonej do światowej sieci zakłada, że każdy chętny instaluje na swojej maszynie wersję modelu, która bada wpływ wybranego parametru. Przeważnie zajmuje to 3 miesiące pracy maszyny „w tle”, nie spowalniając zbytnio pracy komputera.
Obliczenia przeprowadzane są w trzech częściach. W pierwszej używa się danych z lat 1850 – 1900, sprawdzając przewidywania z prawdziwymi odczytami temperatur; część ta nosi nazwę kalibracji. W części drugiej uruchamiana jest symulacja przy pomocy danych od roku 1901 do chwili obecnej. Część trzecia dokonuje symulacji klimatu na lata 2000-2100, zmieniając tylko jeden parametr, np. badając wpływ na klimat niestabilności w cyklu siarkowym. Po zakończeniu pracy, wyniki przesyłane są automatycznie do Biura Meteorologicznego Wielkiej Brytanii przy następnym logowaniu się do sieci. Interfejs oprogramowania do indywidualnego komputera dostarczany jest bezpłatnie. Użytkownik komputera może oglądać wykres pokazujący aktualnie obliczone zmiany klimatu. Zmiany temperatury spowodowane porami roku, długością i szerokością geograficzną, jak i wysokością również mogą być zobrazowane. Te właściwości oprogramowania są idealne do użycia w szkole np. jako interdyscyplinarne projekty w czasie lekcji nauk przyrodniczych ( tłum. matematyka, fizyka, geografia, biologia)
W następnym wydaniu „Science In School” autor przedstawi kilka doświadczeń chemicznych związanych z tematem zmian klimatu.
Web References
- w1 – interaktywną wersję prostego modelu zmian klimatu można znaleźć na stronie: www.chemlabs.bris.ac.uk/outreach/resources/simple_climate_model/index.html
- w2 – więcej o tym eksperymencie, jak się dołączyć; znajdziesz na stronie: http://climateprediction.net.
- Strona Sieci Prognozowania Klimatu zawiera wiele informacji i źródeł szczególnie przydatnych dla szkół. Wiadomości te dostępne są w języku angielskim i hiszpańskim: http://climateprediction.net/content/resources-schools
Resources
- Harrison T, Shallcross D, Henshaw S (2006) Detecting CO2 – the hunt for greenhouse-gas emissions. Chemistry Review 15: 27-30
- Pacala S, Socolow R (2004) Stabilisation wedges: solving the climate problem for the next 50 years with current technologies. Science 305: 968-972. doi: 10.1126/science.1100103
- Shallcross D (2006) Dirty Air. Education in Chemistry, 43 (5): 131-135
- Wiele uwag dla nauczycieli przygotowanych przez autora na temat zanieczyszczeń powietrza, zmian klimatu, zaniku warstwy ozonowej można znaleźć tutaj: www.chemlabs.bristol.ac.uk/outreach/resources/Atmos.html
- Wspaniałym źródłem danych, obrazów itd. związanych z tematem tego artykułu można znaleźć: www.grida.no/climate/vital/index.htm
- Dane ze Stacji Globalnego Laboratorium Monitorowania dotyczących Systemu Badania Ziemi można znaleźć pod adresem: www.cmdl.noaa.gov
- Strona Międzyrządowego Panelu Zmian Klimatu zawierająca dane i raporty dotyczące zmian klimatu w roku 2007 znajduje Si e pod adresem: www.ipcc.ch
- Haubold B (2008) An Inconvenient Truth. Science in School 9: 72. www.scienceinschool.org/2008/issue9/inconvenient
Review
Modelowanie zmian klimatu może stać się jednym z ważniejszych i ciekawszych punktów w programie nauczania w szkołach średnich w całej Europie. Zwłaszcza po kampanii Al Gore’a temat ten zyskał rozgłos światowy i uznanie. Potrzebne materiały, podstawy teoretyczne, informacje nie były zawsze łatwo dostępne, zwłaszcza dla nauczycieli przedmiotów przyrodniczych. Zmieniło się. W artykule tym autorzy oferują szeroki wachlarz szeroki zakres informacji (odnośniki literaturowe). Ten dwuczęściowy artykuł przedstawia skomplikowane procesy w przejrzystej formie.
Model matematyczny najlepiej jest omówić i wypróbować z młodzieżą powyżej 16 lat ( tłum. w polskich warunkach, przełom gimnazjum i liceum). Podstawy fizyczne można z 15- latkami lub młodszymi. Źródła informacji dostępne w sieci wspomniane w artykule bardzo pomagają w przyswojeniu zagadnienia; są to zdjęcia, wykresy, aplety, programy bardzo pomocne w pracy nauczyciela
Tobias Kirschbaum, Niemcy





