Geometria te poate duce pe Lună Teach article
Tradus de Mircea Băduţ. Vom măsura distanţa de la Pământ la Lună folosind geometria şi datele de la o reţea internaţională de şcoli şi observatoare.

spaţiu
Pentru imagine mulţumim
NASA
Să ne imaginăm că întidem braţul şi ne uităm la degetul mare, mai întâi cu un ochi, apoi cu celălalt. Deplasamentul aparent al degetului relativ la fundal se numeşte paralaxă. Acelaşi principiu se aplică dacă două şcoli diferite se ‘uită’ la Lună: fiecare o va vedea cu un pic de deplasament în raport cu stelele din fundal.
În activitatea educativă propusă aici, şcoli din diferite continente se împerechează astfel încât elevi de 16-19 ani pot să-şi compare şi coreleze observaţiile referitoare la Lună pentru a calcula distanţa de la Pământ la satelitul său natural (figura 1). Echipaţi doar cu o cameră foto decentă şi cu o bună cunoaştere a geometriei, observaţiile vor necesita aproximativ 2 ore de clasă, iar calcularea datelor alte 3 ore. (Însă stabilirea parteneriatului între echipe poate lua mai mult timp…).
Definirea condiţiilor corecte
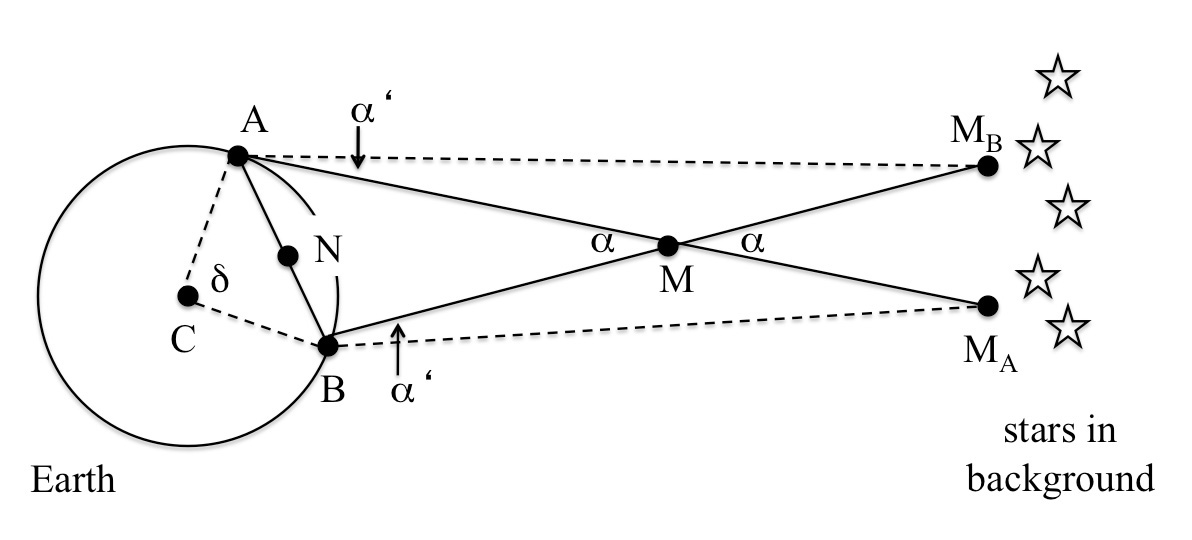
Planul de observare pentru această activitate este detaliat în figura 1, unde M este Luna, reprezentată ca un punct deoarece mărimea ei este foarte mică în comparaţie cu distanţa calculată (aproximativ 1/100).
La fel ca în multe cercetări științifice, şi aici cheia stă în planificare. În cazul de față, pe lângă definirea condițiilor propice pentru realizarea observațiilor, profesorul trebuie să determine (şi să explice) ce marjă de eroare este acceptabilă: lucrul este important pentru ca elevii să nu fie dezamăgiți dacă nu găsesc distanța exactă. Mai jos avem o listă cu aspecte importante de evidențiat atunci când se discută activitatea cu clasa, aspecte utile şi când se stabileşte parteneriatul cu cealaltă școală/organizaţie.
Pentru imagine mulţumim autorilor
Figura 1 arată cum doi observatori (A şi B) văd Luna, M, ca fiind în poziţii uşor diferite ale cerului. Deşi în practică punctele implicate – punctele de observaţie (A şi B), M şi centrul Pământului (C) – nu se află în acelaşi plan, pentru a simplifica lucrurile şi pentru a putea folosi calcule trigonometrice, vom presupune că ele sunt coplanare.
bolta cerească
Pentru imagine mulţumim
Nicola Graf
Pentru ca această aproximare să fie cât mai exactă, cele două puncte de observaţie trebuie să aibă aceeaşi longitudine, iar Luna trebuie să se afle în cel mai înalt punct (în culminaţie)w1 la momentul efectuării observaţiei. Această situaţie este foarte dificil de obţinut, dar vă recomandăm să vă apropiaţi cât mai mult de această cerinţă, și să fiţi conștienți de erorile semnificative implicate de abaterile de la aceasta.
Mai mult, dacă unghiul dintre Lună şi ecuatorul celest (declinaţia)w1 este egal cu media latitudinilor punctelor A şi B, atunci ABM formează un triunghi isoscel, şi aceasta va face calculele şi mai simple.
Un cer de fundal cât mai bun
Vom mai avea nevoie şi de cel puţin două stele strălucitoarew1 (sau planete) în fundal, pentru a determina cele două poziţii aparente ale Lunii, MA şi MB.
Prespupuneri şi ipoteze geometrice
Apoi vom considera că cele două linii drepte AMA şi BMA sunt aproape paralele, aşa cum sunt şi segmentele AMB şi BMB. Aceasta înseamnă că unghiurile α ≈ α’ (figura 1). Deşi nu este adevărată în mod absolut, presupunerea este acceptabilă, întrucât perechea de linii are punctul de convergenţă departe de Pământ şi de Lună. Desigur, deoarece figura 1 nu este desenată la scară, în schemă aspectul pare departe de adevăr.
Dacă măsurăm unghiul α şi distanţa AB – segmentul acesta fiind linia de bază – plus oricare alt unghi din triunghiul ABM, putem apoi calcula toate celelalte distanţe. În mod particular, am putea face triunghiul ABM să fie isoscel, şi atunci cunoaşterea lui a şi a bazei AB ar fi suficientă pentru a calcula toate distanţele.
Esenţial în această triangulaţie este ca linia de bază să fie cât mai lungă (suficient de lungă, în comparaţie cu distanţa pe care dorim să o determinăm), pentru a evita ca deviaţia de paralaxă să fie nesemnificativă. Pentru a determina distanţa până la Lună, se recomandă o distanţă de minim 1000 km între perechea de şcoli partenere.
Însă vor fi erori…
În ciuda încercărilor noastre de a alege condiţiile cele mai bune, măsurătorile nu vor fi perfecte. Principalele surse de eroare sunt:
- Imprecizia de punctare a decalajului Lunii în cele două imagini, în principal din cauza supraexpunerii luminoase a discului Lunii;
- Punctele A, B, C şi M nu sunt chiar coplanare;
- Distorsiuni datorate lentilelor camerei foto;
- Condiţiile de observare;
- Refracţia atmosferică;
- Sincronizarea temporală a măsurătorilor.
Erorile d) şi e) nu sunt foarte importante: măsurătoarea este bazată pe unghiuri largi, astfel că nu este afectată semnificativ de imprecizia a câtorva secunde de arc.
Sincronizarea temporală a măsurătorilor (f) nu este nici ea foarte importantă, deoarece Luna se deplasează într-o oră cu o distanţă echivalentă cu diametrul propriu, aşa încât o desincronizare de câteva secunde (sau chiar de câteva minute) nu este importantă.
Distorsiunile optice din obiectivul camerei foto (c) pot fi reduse dacă se foloseşte un unghi de vizualizare mic, ca la teleobiective. O cameră foto uzuală adaugă o eroare mare, dar totuşi acceptabilă. În cazul nostru, unghiul nu a fost destul de mic, şi am estimat o eroare de aproximativ 1-2%.
Erorile datorate surselor a) şi b) sunt cele mai importante şi fiecare poate adăuga o imprecizie de 5-10%. Împreună, ele vor conduce la o eroare cumulată de 10-20%. Pentru a reduce a) trebuie să alegem o linie de bază cât mai lungă, astfel încât decalajul de paralaxă al Lunii să fie cât mai mare; pentru a reduce b) trebuie să alegem judicios locaţiile şi momentele pentru observaţie, astfel încât punctele A, B, C şi M să fie în acelaşi plan. Dacă ambele condiţii sunt îndeplinite (pentru experimentul nostru prima condiţie s-a îndeplinit, însă a doua nu), eroarea poate fi redusă până la câteva procente.
Reţeaua paralaxă
Am pregătit o reţea de şcoli, observatoare şi de profesori pe întinsul globului pentru a realiza această măsurătoare. Reţeaua constă din următorii membri:
- Mario Koch, profesor la Liceul Friedrich-Schiller din Weimar, Germania
- Noorali Jiwaji, lector de fizică la Open University of Tanzania, din Dar es Salaam, Tanzania
- Frank Oßwald, profesor la Goethegymnasium din Weissenfels, Germania
- Matthias Penselin, profesor la Albert Schweitzer Gymnasium Crailsheim şi la House of Astronomy din Heidelberg, Germania
- Alexander GM Pietrow, Iosto Fodde şi Jelle Mes, studenţi la Observatorul din Leiden şi membri ai comitetului de observaţii Astronomisch Dispuut ‘F. Kaiser’, Leiden, Olanda
- Elena Servida, profesor la Liceul Vittorio Veneto in Milan, Italia
- Brian Sheen, Observatorul Roseland, St. Austell, Mare Britanie
Folosind fie această reţea, fie propria reţea liber constituită, profesorii pot ajuta la obţinerea datelor necesare la derularea observaţiilor lunare pentru ca elevii să poată calcula distanţa de la Pământ la Lună.
Distanţele dintre centrele din reţeaua constituită de noi asigură linii de bază (distanţe AB) suficient de mari pentru a face posibilă măsurarea distanţei de la Pământ la Marte în luna mai 2016 (Cenadelli et al, 2009; Penselin et al, 2014). În luna mai, Terra va fi situată între Soare şi Marte, iar Marte va fi la cea mai mică distanţă de Pământ, fiind o poziţie ideală pentru astfel de măsurători.
Dacă veţi dori să contactaţi oricare dintre centrele acestei reţele internaţionale pentru a efectua măsurători, luaţi legătura cu Davide Cenadelli prin adresa de email davide.cenadelli@unimi.it
Materiale
Singurul material specific necesar este o cameră foto bună pentru a fotografia Luna pe cer. (Şi eventual un trepied pentru a sprijini camera foto pe durata fotografierii.) Un obiectiv telefoto, cu distanţa focală 100–200mm, ar fi de preferat, însă şi un obiectiv normal va funcţiona dacă stelele sau planetele din fundal nu sunt foarte apropiate de Lună.
Procedura de lucru
- Folosiţi reţeaua de paralaxe (vedeţi caseta) pentru a găsi o şcoală sau un observator care se află pe o longitudine similară şcolii dumneavoastră.
- Notaţi latitudinea şi longitudinea celor doi parteneri (l = latitude, l = longitude). Aici noi am folosit observaţii preluate în Cape Town, Africa de Sud, şi Observatorul Astronomic al Regiunii Autonome a Văii Aosta (OAVdA), Italia:
OAVdA, Italy: (λI 45.78° N, lI 7.48° E)
Cape Town, Africa de Sud: (λS 33.93° S, lS 18.42° E) - Puneţi de comun acord datele şi orele la care se vor face observaţiile asupra Lunii (este recomandat să planificaţi mai multe date, pentru eventualitatea unor condiţii meteo nefavorabile). Cei doi observatori de mai sus au fost de acord să facă observaţiile simultane pe 2 februarie 2015, la ora 20.02. În acea seară au fost două corpuri cereşti luminoase alese ca referinţă, Jupiter şi Procyon (α CMi), aflate pe cer nu departe de Lună, servind astfel ca puncte de referinţă pentru măsurarea poziţiei Lunii.
Cele mai favorabile condiţii sunt când corpurile alese (planete luminoase sau stele, precum Jupiter şi Procyon) sunt vizibile pe fundal lângă Lună, şi cât mai aproape de aceasta, astfel încât să putem folosi un obiectiv foto cu distanţă focală lungă. Acest fapt va evita efectele de distorsiune optică specifice obiectivelor foto largi. - La data stabilită, toţi participanţii cu cer senin vor realiza câteva fotografii ale Lunii, urmând orarul planificat. Imaginile trebuie să arate cât mai clar posibil Luna şi cele două corpuri cereşti alese ca referinţă. Trebuie captate mai multe imagini foto, cu timpi de expunere diferiţi, pentru a putea alege apoi imaginea care asigură cel mai bun compromis între o Lună nu prea strălucitoare şi corpurile din fundal.
- Suprapuneţi imaginile alese din cele două observaţii într-o singură imagine, ca în figura 2.

Pentru imagine mulţumim autorilor
- Măsuraţi distanţa dintre Jupiter şi Procyon pe o imagine, şi rescalaţi cealaltă imagine astfel încât acea distanţă să coincidă – astfel cele două imagini sunt aduse la aceeaşi scară;
- Suprapuneţi imaginile şi marcaţi poziţiile Lunii aşa cum a fost ea văzută de cele două şcoli.
- Măsuraţi deplasamentul centrelor de Lună.
- Calculaţi linia de bază a paralaxei, AB, ca în figura 1.
Unghiul d, dintre cei doi observatori A şi B, poate fi calculat astfel (Roy & Clarcke (1977):
cos d = sin λI sin λS + cos λI cos λS cos(lI − lS )
= −sin (45.78°) sin (33.93°) + cos (45.78°) cos (33.93°) cos (10.94°)
= 0.1681
Deci δ = 80.32° (1)
Dacă presupunem că Pământul este perfect sferic şi că raza sa este de 6367 km, atunci linia de bază AB este dată prin:
AB = 2BN
= 2(CB * sin (δ/2))
= 2 × 6367 km × sin (80.32°/2)
= 8212 km (2) - Calculaţi unghiul de paralaxă, α.
Prin simpla folosire a unei rigle, putem estima că deplasamentul Lunii observat astfel (figura 2) este de aproximativ 2,4 ori mai mare decât diametrul lunar. Văzut de pe Pământ, diametrul lunii este cuprins într-un unghi de 0,5°; asta înseamnă că dacă “trasăm” două linii de la ochii unui observator la extreme diametrale ale lunii, unghiul dintre aceste linii este de 0,5°.
Dacă diametrul lunar corespunde unghiului de 0,5° şi deplasamentul aparent al Lunii pe observaţiile noastre este de 2,4 ori mai mare decât diametrul lunar, atunci:
α = 2.4 * 0.5 = 1.2° - Calculaţi distanţa dintre Lună şi centrul Pământului, CM.
Vom calcula CM în două situaţii. În ambele cazuri vom considera că punctele A, B, M şi C sunt coplanare.
Cazul 1: ABM este triunghi isoscel
În acest caz unghiurile BAM şi ABM sunt egale, şi:
CM = CN+NM
= CA cos δ/2 + ([AB/2]/[tan α/2])
= 4866 + 392 080 km
= 396 900 km (3)
Distanţa calculată la momentul măsurătoriiw1 a fost de 397 900 km, deci am obţinut o valoare subestimată cu cel mult 0,3%. Considerând aproximaţiile folosite, precizia bună a măsurătorii a fost în parte o chestiune de noroc.
Cazul 2: ABM nu este triunghi isoscel
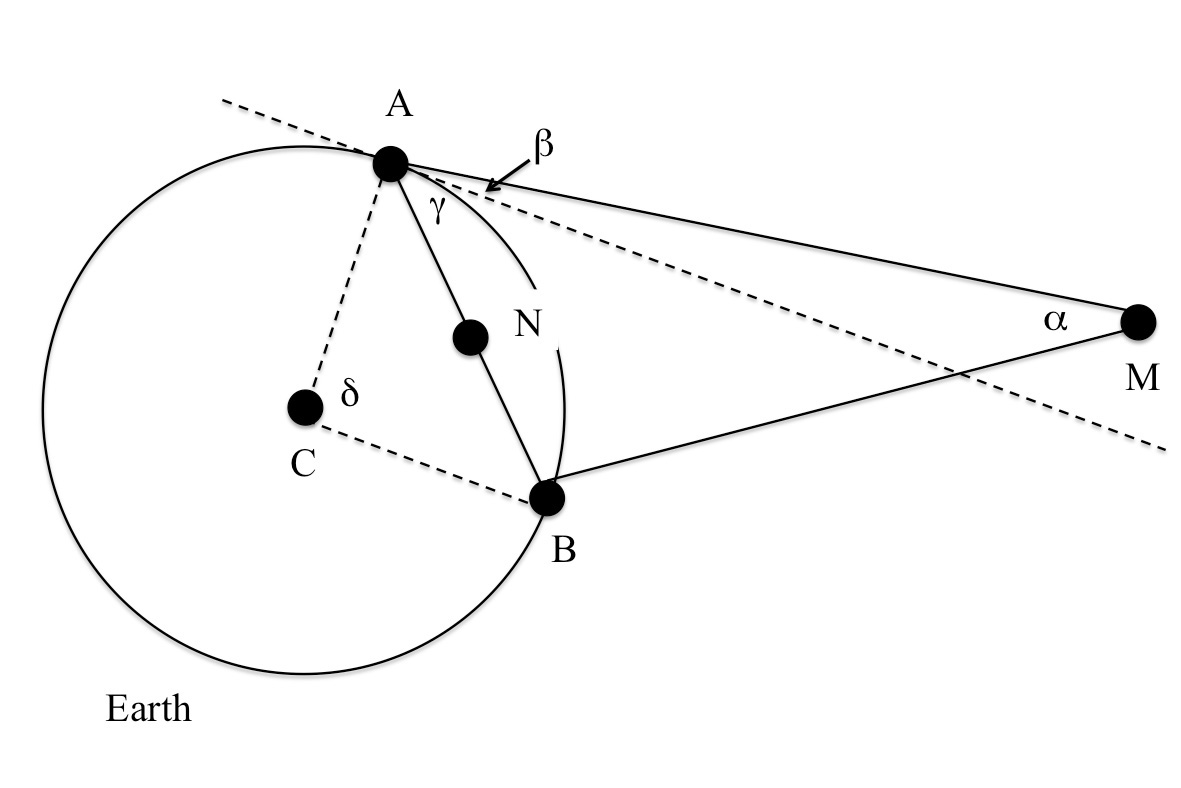
Figura 3: Detaliu al secţiunii prin figura 1 arătând spaţiul dintre Pământ şi Lună, şi unghiurile β şi γ
Pentru imagine mulţumim autorilorDacă renunţăm la presupunerea că AMB este triunghi isoscel, trebuie să aflăm valoarea unui alt unghi, precum BAM. Unghiul BAM este egal cu suma dintre β, referitor la altitudinea Lunii deasupra orizontului din A, şi γ (vedeţi figura 3). β poate fi măsurat cu un echipament adecvat, sau, în lipsă, îl putem considera aproape agal cu altitudineaw1 uneia dintre stelele sau planetele de referinţă folosite pentru a măsura deplasamentul Lunii. Pentru Procyon, avem β = 39,3°.
Putem calcula unghiul γ folosind valoarea pentru d pe care am determinat-o mai devreme, pentru că regula geometrică spune că: γ = d/2.
De unde rezultă că BAM = β + γ = 79,5°.
La final, dacă aplicăm formula lui sinus în triunghiul ANM, obţinem:
ΝM/sin79.5° = AN/sin(α/2)
ΝM = AN (sin79.5°/sin0.6°)
≈ 385 536 km (4)
şi astfel:
CM = CN + NM
= CAcosα/2 + NM
= 4866 + 385 536 km = 390 400 km (5)
Rezultatul obţinut este acceptabil, fiind cu doar 1,9% mai mic decât valoarea cunoscută.
Recunoaşteri
Autorii doresc să mulţumească cu căldură tuturor participanţilor la reţeaua de observaţii, precum şi elevilor care au participat la ESO Camp 2014 şi care au realizat măsurători similare.
Observatorul Astronomic al Regiunii Autonome a Văii Aosta este sprijinit de Guvernul Regional al Văii Aosta, de municipalitatea orașului Nus și de Comunitatea Mont Emilius. Andrea Bernagozzi a efectuat o parte din munca acestui proiect în timp ce era susţinut de un grant din partea Fondului Social European al Uniunii Europene, de Regiunea Autonomă Valea Aosta și de Ministerul italian al Muncii și Politicii Sociale.
References
- Cenadelli D et al. (2009) An international parallax campaign to measure distance to the Moon and Mars. European Journal of Physics 30: 35-46
- Penselin M, Liefke C, Metzendorf M (2014) Zweifacher Blick auf erdnahen Asteroiden. Sterne und Weltraum 11: 72-77
- Roy AE, Clarcke D (1977) Astronomy: Principles and Practice. Bristol, UK: Adam Hilger. ISBN: 0852743467
Web References
- w1 – Pentru a găsi valorile necesare realizării calculelor descrise în articol, puteţi folosi simulatorul ceresc Stellarium, un planetariu open-source pe calculatorul personal.
Resources
- Metoda folosită în acest articol este descrisă în multe cărţi de astronomie. De exemplu:
- Karttunen H et al (2007) Fundamental Astronomy 5th edition. Berlin, Germany: Springer. ISBN: 9783540341437
- Un material didactic legat de Penselin et al (2014), care poate fi direct folosit la această activitate educativă, poate fi găsit pe web-site-ul Wissenschaft in die Schule (doar în limba germană).
Review
Articolul de faţă descrie o cale plăcută de a aduce împreună matematica şi alte ştiinţe, precum astrofizica. El arată cum putem calcula distanţa până la Lună sau chiar până la Marte, folosindu-ne de datele proprii luate cu o cameră foto şi de date provenind de la o instituţie parteneră (precum cele din reţeaua de paralaxe). Folosind matematica – sau matematicile aplicate, de vreme ce rezolvăm o problemă reală – vom ajunge la rezultate bune.
Datorită introducerii sale scurte dar eficiente, articolul poate fi folosit atât de profesorii de ştiinţe cât şi de cei de matematică.
Gerd Vogt, Şcoala Secundară Superioară pentru Mediu şi Economie, Yspertal, Austria





