Supporting materials
Download
Download this article as a PDF

La pandemia del COVID-19 ha posto l'accento sul fenomeno della crescita esponenziale. Questo fornisce l'opportunità di insegnare questo concetto complicato nel contesto di un fenomeno reale.
La diffusione estremamente rapida del virus del COVID-19 non è così sorprendente come si potrebbe pensare a prima vista. È una conseguenza della crescita esponenziale nella propagazione del virus, che è difficile da afferrare intuitivamente.
Le attività descritte qui di seguito sono state concepite per studenti di età dai 14-16 anni e possono essere completate in 45 minuti.
Se un approccio più semplice potrebbe essere maggiormente adatto alla vostra classe, potete utilizzare l’articolo per studenti di età 11-13 anni he accompagna questo, Exponential growth 1: learn the basics from confetti to understand pandemics. Quest’articolo include anche un breve confronto con la crescita lineare.
Nel corso di queste attività, gli studenti impareranno differenti tipi di crescite esponenziali e di come classificarle utilizzando il fattore R. Nel contesto della pandemia di COVID-19, identificheranno come la crescita può rallentare ed utilizzeranno una simulazione per esplorare quali azioni condizionano il corso della pandemia.
I calcoli per le tavole possono essere semplificati utilizzando una calcolatrice oppure il foglio Excel. Tavole e sistemi di coordinate per il completamento sono sul foglio di lavoro.
Una leggenda sull’invenzione degli scacchi rivela quanto velocemente i numeri possano salire alle stelle per la crescita esponenziale. Si racconta che il re Indiano Shihram, che si suppone sia vissuto nel terzo o quarto secolo DC tiranneggiando il suo popolo, aveva spinto la sua nazione in miseria. Per portare alla attenzione del re le sue colpe senza suscitarne la sua ira, il gran visir Sissa ben Dahir inventò un gioco nel quale il re, il pezzo più importante, non poteva fare nulla senza l’aiuto di altri pezzi. L’insegnamento degli scacchi suscitò una grande impressione su Shihram. Egli si addolcì e pubblicizzò in lungo e in largo il gioco degli scacchi. A ringraziamento della bella lezione e del divertimento, concesse al gran visir di esaudire un desiderio, il quale chiese solamente:
“Un chicco di riso, che rappresentava il primo quadrato della scacchiera. Due chicchi per il secondo quadrato. Quattro chicchi per il successivo. Quindi per l’ottavo, 16, 32 raddoppiando per ogni successivo quadrato sino al 64esimo e ultimo quadrato.”
Il re fu impressionato dalla apparente modesta richiesta, e immediatamente esaudì la richiesta. Perché commise un così enorme errore?
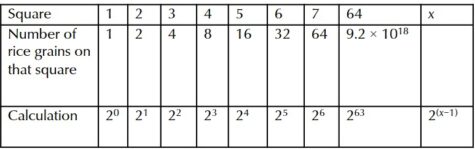
Permettete agli studenti di leggere le informazioni base sul foglio di lavoro circa il raccolto annuale medio di riso e di discutere sulla quantità di riso che il gran visir ha richiesto.
L’incremento del numero di chicchi di riso da un quadrato al successivo non è costante, come succede in una crescita lineare, ma aumenta a seconda del numero di chicchi di riso sul precedente quadrato. Se l’aumento dipende dalla quantità attuale e perciò non è costante, si parla di crescita esponenziale. Se la quantità considerata è piccola, anche l’aumento sarà piccolo, conseguentemente la quantità crescerà lentamente. Tuttavia, la quantità aumenta di continuo, e altrettanto crescerà l’aumento, che così può diventare molto grande molto velocemente.
In una malattia infettiva, il numero di nuove persone infettate può crescere così rapidamente come la quantità di riso sui quadrati della scacchiera dell’Attività 1. La diffusione della malattia infettiva spesso segue un medesimo modello, che può essere descritto solo con alcuni parametri.

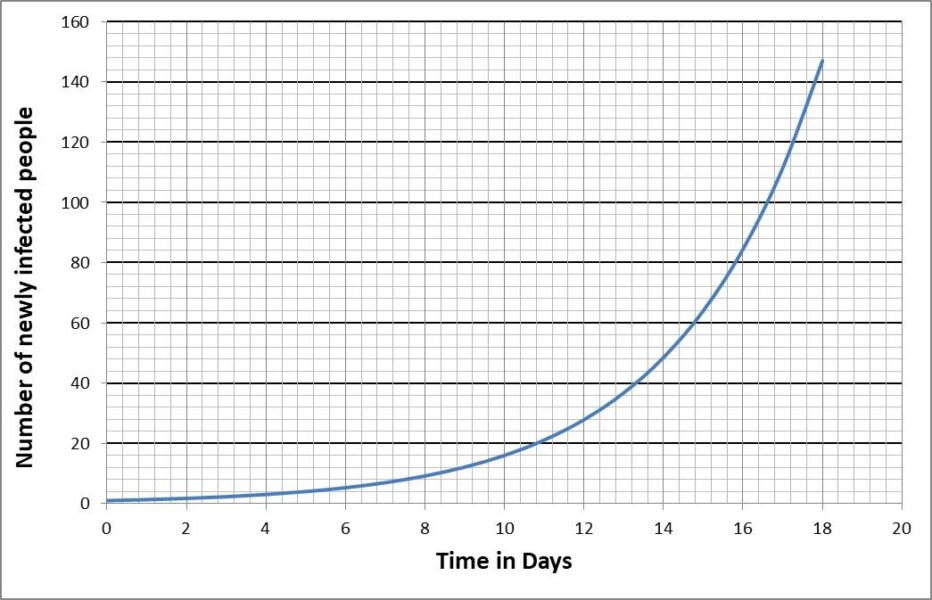
Per ricavare l’esatto tempo di raddoppio per il caso discusso sopra, era possibile usare la radice quadrata solamente a causa della base speciale, quattro. Chiedere agli studenti come ricavare il tempo di raddoppio in forma più generale.
Nel caso generale, si deve ricorrere al logaritmo. Se gli studenti non sono ancora familiari con il concetto di logaritmo potrete introdurlo a loro come segue.
Importante informazione di base: proprio come la radice quadrata si utilizza per risolvere l’equazione x×x = 2, la cui soluzione è x = ± √2 ~ 1.414, la notazione simbolica è usata per risolvere l’equazione 2x = 6, che è x = log26 (logaritmo in base 2 di 6). Il valore numerico si ricava con l’aiuto della calcolatrice tascabile: log26 ~ 2.585.
Il valore esatto del tempo di raddoppio T1/2 , si può ricavare come segue:
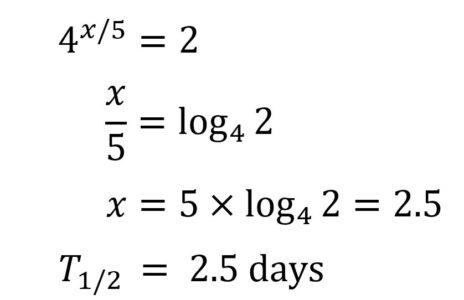
In generale: T1/2 = D × logR2
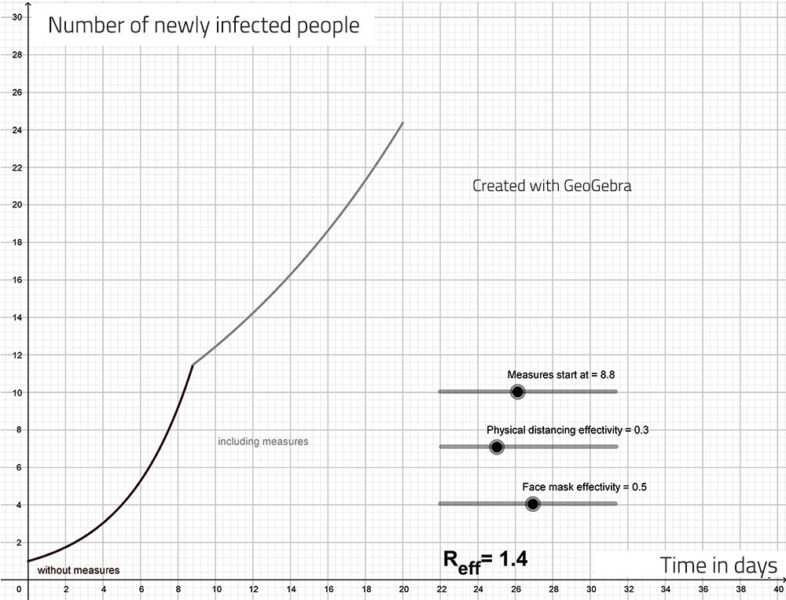
Gli studenti dovranno leggere le informazioni di base riportate sul loro foglio di lavoro per stabilire come varia il valore R con l’immunizzazione. Saranno in grado di calcolare la percentuale della popolazione che necessita l’immunizzazione affinché si contenga la diffusione, per esempio, ridurre il reale valore di R ad uno. Il risultato dovrebbe essere il 75%.
Confrontate la percentuale della popolazione che necessita di essere immunizzata per raggiungere l’immunità di gregge per il COVID-19 (R0 = 4) rispetto al morbillo (R0 = 15) e la poliomielite (R0= 6) e discutete con loro sulla sfida posta dalla campagna di vaccinazione associate. I risultati sono del 75% (COVID-19, 93% (morbillo), e 83% (polio).
Download this article as a PDF