Supporting materials
A képi objektumok fizikai tulajdonságainak vizsgálata (Word)
A képi objektumok fizikai tulajdonságainak vizsgálata (Pdf)
Download
Download this article as a PDF

Fordította: Gálicza Judit. A látás élességének meghatározásához nemcsak biológiai kísérletek, hanem mögöttes fizikájának megértése is szükséges.
A látásélesség egy érték. Megmutatja mennyire éles a látásunk, legfőképpen mennyire jól tudjuk elkülöníteni az apró részleteket. Az optikusok ezt úgy állapítják meg, hogy megkérnek minket olvassunk fel egy vizsgálótábláról mindaddig, míg a betűk annyira kicsik nem lesznek, hogy már nem tisztán kivehetőek a számunkra.
A retinában lévő fotoreceptorok sűrűsége az egyik biológiai faktor, amely meghatározza a látásélességet (lásd a ‘Hogyan működik a szemünk’ dobozban). Ez viszont felvet egy érdekes kérdést: élesebbé teheti látásunkat a retina receptorsűrűségének növelése? Hogy megválaszolhassuk a kérdést, meg kell vizsgálnunk úgy a látórendszer biológiáját, mint a fény fizikáját. A téma része a legtöbb középiskolai biológia és fizika tananyagnak, a tárgyak viszont hagyományosan külön vannak tanítva, gyakran a diákok profilja is különböző. Ezzel szemben, az itt javasolt tantárgyközi megközelítés lehetőséget ad a diákoknak arra, hogy mélyebb betekintést nyerjenek a látásélesség biológiájába, fizikájába, illetve a következő fontos, általános üzenetet közvetíti: sok probléma a modern tudományban csapatmunkával és interdiszciplináris együttműködéssel oldható meg a begjobban.
A cikk bemutat egy egyszerű módszert arra, hogyan számítsuk ki a szem felbontóképességét, meghatározva a látásélességet egy általunk készített vizsgálótábla segítségével. Ezzel a módszerrel megbecsüljük a retinán azt a legkissebb távolságot, amikor még két pont képét két, teljesen elkülönített tárgyként vagyunk képesek beazonosítani. Egy további, a kiegészítő anyagban található kísérlet ezt a távolságot a fény fizikai tulajdonságai alapján a látásélesség elméleti korlátaira vonatkoztatja.
A két feladat16-19 év közötti diákoknak a legmegfelelőbb; körülbelül két-két órát vesz igénybe, beleértve az előkészületeket és az adatok feldolgozását. További két óra lehet az eredmények megbeszélése.
A tárgyakról visszaverődő fénysugarak a pupillán keresztül jutnak a szembe. A szem négy alkotórésze – szaruhártya, szemlencse, szemcsarnok és üvegtest – a szemgolyó hátsó felületére, a retinára (ideghártya) fókuszálja a fénysugarakat, (1. ábra). A retina több rétegből áll. Az egyik réteget milliónyi fényérzékeny fotoreceptor alkotja. Ezek továbbítják a jelt a ganglionsejteken keresztül az agyba. A fotoreceptorok specializált idegsejtek. Két csoportra, a csap- és pálcikasejtek (alakjuk szerint megnevezve) csoportjára vannak osztva. A csapsejtek leginkább a retina közepében helyezkednek el. Világosban éles-, színes látást tesznek lehetővé. A pálcikasejtek a retina szélei felé találhatóak. Segítenek minket a mozgás érzékelésében, a kis fényerőnél történő látásban, valamint perifériás látást tesznek lehetővé. Sűrűségük a retinában (a látógödörben számuk meghaladhatja a 200 000 sejt/mm2) fontos szerepet játszik a látásélessében.
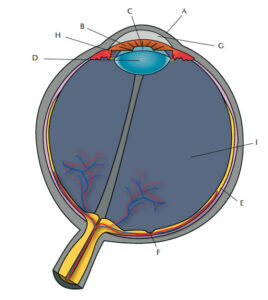
Az emberi szem szögfelbontása két, tisztán elkülöníthető pont közti legkissebb szögnek felel meg, amely érték kapcsolatban van a retinában található fotoreceptorok sűrűségével. Tipikusan 1 ívperc (egy fok 1/60-od része). Ebben a feladatban a szögfelbomtást a két pont közti távolság, illetve a megfigyelő és a pontok közti távolság arányából számítjuk ki. Mivel a szögfelbontás nagyon kis értékeket feltételez, ez a leegyszerűsített matematikai eljárás (a sokkal bonyolultabb, α szög tangensének kiszámíta helyett, lásd 2. ábra) jól használható. A matematikában ezt a lerövidítést kis szög közelítésnek nevezik. A számított arányt ezután a retinára vetített két pont közti távolság meghatározására használjuk, ahogyan a 2. ábrán is látható.
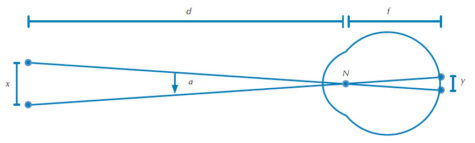
d = a tárgy és a tesztszemély szeme közti távolság (ebben a kísérletben a vizsgálótábla); f = az egyszerűsített szem fókusztávolsága; x = a két pont között érzékelhető legkisebb réstávolság (a kísérletben két fekete vonalat elválasztó legkissebb réstávolság egy megszakított vonalon); y = ennek a két pontnak a távolsága a retinán; N = csomópont.
A képet Günther KH Zupanc szíves hozzájárulásával közöljük
A diákok egy-egy vizsgálótáblát fognak készíteni egyszerű fekete vonalsorozatokból, melyeket különböző szélességű szünetekkel választanak el. Ezután kérjük meg, hogy állapítsák meg melyik vonal tűnik megszakítottnak és melyik folyamatosnak, majd felhasználva a kapott adatokat számítsák ki a megközelítőleges szögtávolságot, és így a receptorok távolságát a szemben.

Az emberi szem szögfelbontása tipikusan 40 szögmásodperc és 1 ívperc között változik. Ahhoz, hogy két különálló pontot el tudjunk különíteni egymástól, legalább három, sorban elhelyezkedő fotoreceptorra van szükségünk: egy-egyre, hogy érzékeljék a két pontból érkező fényt és egy harmadikra, hogy érzékelje a réseket. Egy ívperc felbontáshoz (ami 1 km távolságból 0.3 m-nek felel meg) a retinára vetített képek körülbelül 6 μm távolságra vannak egymástól. Ez azt jelenti, hogy két receptor középponttól-középpontig tartó távolsága 3 μm. Egy 40 szögmásodperces felbontáshoz ez a távolság két pont között körülbelül 4 μm.
A szem aktuális felbontóképessége nem csak a receptorok távolságától függ, hanem a fény megtörésétől is, ahogyan az áthalad a pupillán. A második kísérlet letöltésével ez tovább vizsgálható.
Tehát, javítható a látásélesség a retina csapsejt sűrűségének növelésével?
40 szögmásodperctől 1 ívpercig terjedő felbontás érhető el ha csak egyszerűen mereven nézünk egy tárgyat. A tárgy képe rávetítődik a retina közepén egy specifikus, kizárólag csapsejteket tartalmazó pontra, a látógödörre (favea vcentrálisra). A csapsejtek sűrűsége itt sokkal nagyobb, mint bárhol máshol a retinában. A sejtek átmérője azonban csak 3 μm (összehasonlítva a retina más területével, ahol 10 μm). Köszönhetően a csapsejteket körül vevő sejt közötti térnek (pl. a tápanyagszállítás zajlik itt) a sejtek középpontól-középpontig mért távolsága körülbelül 4 μm. Ez a csapsejtsűrűség a látógödörben már elég közel van a maximálisan lehetséges elhelyezkedési sűrűséghez.
Ahogy a kiegészítő kísérletben kiderül, a fénytörés, vagyis a legkisseb felbontható távolság értéke két fényforrás között a szemben, körülbelül 5 μm, ami 2.5 μm távolságot feltételez két csapsejt között. A csapsejtek körüli sejt közötti térnek köszönhetően ez az elméletileg várható távolság kiválóan megegyezik a látógödörben lévő csapsejtek közti, körülbelül 4 μm-es távolsággal. Ezért, a csapsejtek sűrűségének növelése biológiai okok miatt lehetetlen lenne, valamint a fény sajátosságai által meghatározott fizikai korlátok miatt, nem vezetne jelentős látásélesség növekedéshez.
A cikk két kísérletet ír le a látásélesség meghatározásával kapcsolatosan, amelyek egy-egy példa a természetben előforduló biológia és fizika közti kapcsolatra. A tantárgyközi tevékenységek még vonzóbbá tehetik a tudományt és lehetőséget biztosíthatnak más tanárokkal való együttműködésre.
Minden, a kísérlethez szükséges alapanyag egyszerűen elérhető, az utasítások könnyen követhetőek, ami alkalmassá teszi arra, hogy a diákok kis csoportokban elvégezhessék a feladatot.
A cikk egy jó kiindulópont lehet arra, hogy beszéljünk a csapatmunka és az interdiszciplináris együttműködés fontosságáról úgy a modern tudomány, mint más területek problémáinak megoldásában.
Mireia Güell, Spain