La escala del Espacio Teach article

Traducido por José L. Cebollada. ¿Cómo miden los astrónomos las distancias entre las estrellas? Podemos usar  en clase un método bastante preciso con una cámara digital para medir el desplazamiento por paralaje.

Los astrónomos miran de lejos, están muy alejados de los objetos que estudian. Y es vital conocer la distancia de los cuerpos celestes y saber qué tipo de objeto es porque nos permite distinguir entre objetos muy lejanos y luminosos, que los percibimos con poco brillo, y los más próximos y menos luminosos. Si no conocemos las distancias una galaxia se puede confundir con una estrella, hasta que comprobamos que una está miles de millones de veces  más alejada que la otra y es billones de veces más brillante.

La paralaje –el cambio en la posición en la que se ve un objeto cuando el observador cambia de lugar- es el método más importante para determinar la distancia de las estrellas desde la Tierra. Podemos percibir la paralaje cuando miramos a través de la ventanilla del tren: los objetos cercanos parecen moverse mucho más rápido que los lejanos. Con este efecto podemos calcular la distancia a un objeto midiendo el cambio aparente de la posición que se produce al desplazarse el observador.

Por supuesto que el reto es la precisión. ¿Cómo podemos hacer medidas precisas por paralaje? En este segundo artículo sobre la paralaje vamos a utilizar un método similar al que utilizan los astrónomos adaptado para su uso en el aula (para leer el artículo anterior, ver Pössel, 2017). En lugar de usar aparatos para medir ángulos (como el descrito en el artículo y que se basaba en medidas con teodolitos) calcularemos la distancia a una ‘estrella’ tomando fotos desde diferentes posiciones y obtendremos los datos necesarios para calcular la distancia a la estrella.

Más adelante se describirá una variante más auténtica y precisa, algo más complicada. Requiere usar un punto fijo de referencia fuera del aula –al igual que los astrónomos  usan lejanos objetos brillantes (como los quásares, unas galaxias muy activas) como puntos fijos de referencia cuando miden mediante paralaje, más que confiar en los datos de sus telescopios que apuntan al mismo punto en cada observación.

Para estas medidas necesitaremos una cámara digital, si es posible, montada sobre un banco óptico (ver figura 1). Las actividades se pueden realizar por grupos. Hay que contar con unos 30 minutos para montar y tomar medidas y otros 30 minutos para el análisis y los cálculos.

Materiales

• Cámara digital con una lente de distancia focal conocida (al menos de 50 mm)
• Banco óptico (o montaje similar para poder mover la cámara y medir la distancia que se ha desplazado lateralmente Puede servir una mesa plana o una regla)
• Modelo de una estrella (una pequeña esfera menor de 1 cm de diámetro o un LED, montado en un soporte)
• Un objeto de longitud conocida con marcas reconocibles (una regla) para calibrar
• Cinta métrica
• Programa de edición de imágenes como Adobe Photoshop o GIMP

Procedimiento

1. Monta la cámara en el banco óptico de manera que se pueda desplazar lateralmente una distancia conocida. La cámara debe enfocar a determinados ángulos al cambiar de posición (figura 1). Si no dispones de un banco óptico puedes colocar una regla sobre la mesa y mover la cámara de posición midiendo la distancia de desplazamiento.
    

2. Monta el modelo de estrellas de manera que quede a la altura de la cámara y a unos metros de distancia del banco.
    
3. Desplaza la cámara hasta un extremo del banco y asegúrate que puedes ver la estrella a través del objetivo. Toma una foto desde esa posición.
    
4. Mueve la cámara hasta otro punto en el que se siga viendo la estrella. Apunta la distancia y toma otra foto desde este punto.
    
5. Mueve la cámara a la posición central. Coloca ahora el objeto de calibración (por ejemplo, una regla) justo delante de la cámara y toma otra foto. Esta es la imagen que servirá para calibrar las medidas.
    
6. Mide con la cinta métrica la distancia desde la cámara hasta la regla.

Calcular la distancia  a la estrella

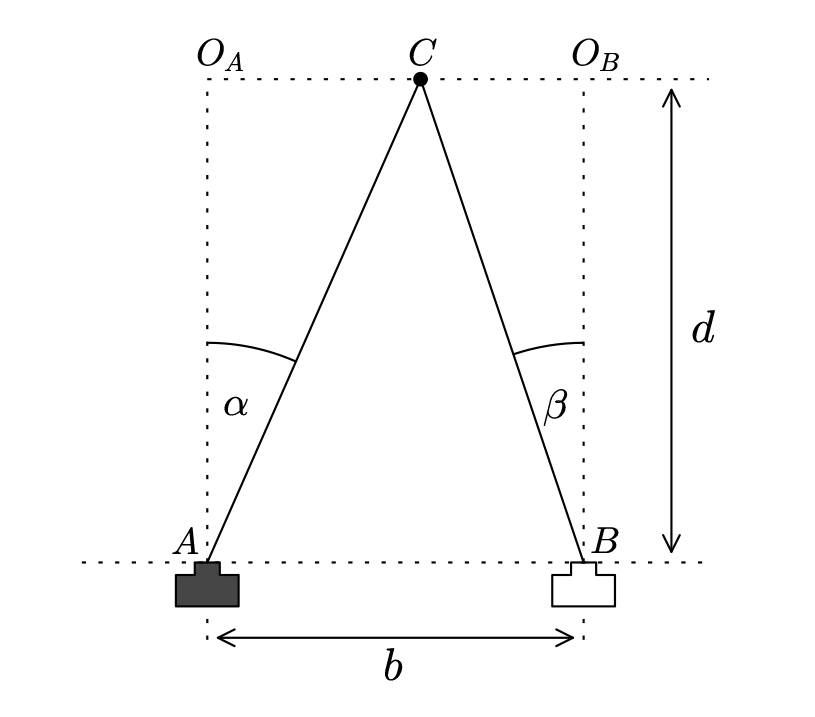
La figura 2 muestra el montaje experimental. b representa el desplazamiento lateral de la cámara (sobre el banco óptico o la mesa) entre la primera y la segunda posiciones (A y B), y C es la posición del modelo de la estrella; d es la distancia desde la línea por la que se mueve la cámara hasta la estrella, es decir, la que queremos calcular.

Para calcular la distancia d se tienen que seguir los pasos siguientes.

1. Si dibujamos una línea paralela a la línea base y a la distancia d de la estrella, la línea de visión de la cámara desde la posición A cortará a la línea en O_A y desde la posición B, en O_B.  Los ángulos entre la línea de visión de la cámara y la dirección hacia la estrella desde las posiciones A y B son α y ß, respectivamente.
    

   

   Las cámaras, al contrario que los teodolitos, no miden ángulos directamente. Por eso necesitamos relacionar la posición de las imágenes de la estrella en el detector de la cámara con el ángulo de los rayos de luz de la estrella en diferentes posiciones de la cámara.
    

2. Para ello plantearemos una situación ligeramente simplificada en este modelo. Primero vamos a considerar que la lente de la cámara es un agujero puntual, como se ve en la figura 3, donde P es la posición de la lente. Así el rayo de la estrella viaja en línea recta hasta el objetivo de la cámara y llega al sensor que está a una distancia f (la distancia focal de la lente) detrás de la lente.
    

   

3. Ahora nos fijamos en la figura 2 y pensamos en qué vería un observador que se moviera con la cámara cuando se desplaza desde A hasta B. En efecto, podemos ver el resultado cambiando la posición A de la cámara (lo que cambia la línea AC) hacia la derecha una distancia b, y ahora las dos coinciden las dos posiciones de la cámara.

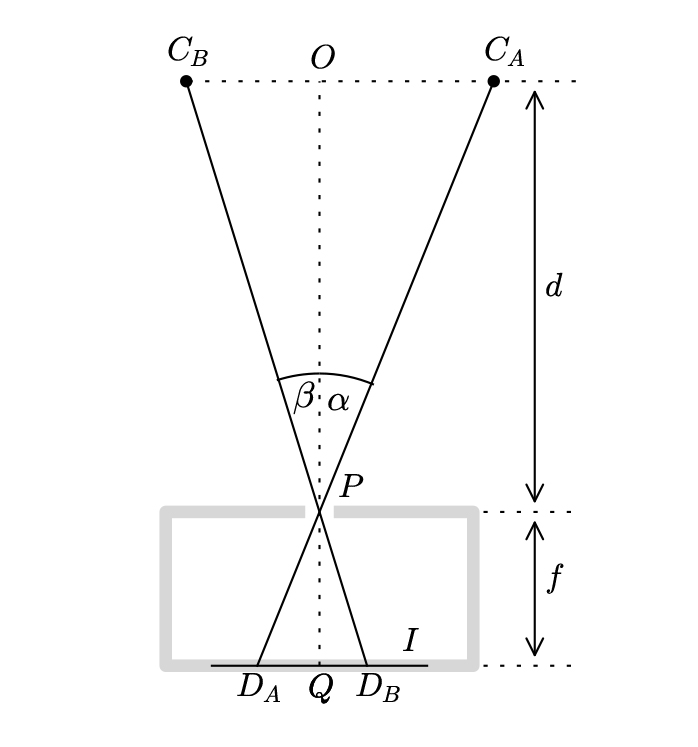
   La imagen 3 muestra la imagen que se ve desde la cámara. La posición aparente de la estrella estará en C_A cuando la cámara está en la primera posición (A) y la imagen se formará en D_A en la pantalla del detector. Del mismo modo, después de mover la cámara hasta B, la posición aparente de la estrella será ahora C_B y la imagen D_B. (El segmento OQ representa la distancia entre el plano que contiene a la estrella y el plano del sensor donde se forma la imagen). La longitud C_BC_A es la distancia b en la figura dos, los ángulos a y ß son los mismos en las dos imágenes.
    

4. Si nos fijamos en la geometría veremos triángulos semejantes. Aplicando esa semejanza obtenemos la fórmula que relaciona la distancia d con las otras longitudes conocidas, b y f y así podemos calcular d. En la sección de materiales adicionales está el detalle del cálculo de la fórmula^w1.

   La formula es:

   
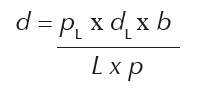
   Donde:

   d = distancia a la estrella
   L = La distancia al objeto de calibración
   b = el desplazamiento de la cámara (que corresponde a la distancia de C_A a C_B)
   d_L = La distancia del objeto de calibración a la línea donde se encuentra la cámara (medida en la línea OQ)
   p = Distancia, medida en número de pixeles entre las imágenes de la estrella (en D_A y D_B)
   p_L= la longitud, medida en píxeles entre de la imagen del objeto de calibración
    

5. Para utilizar la formula se necesita un programa de edición de imágenes para calcular p, el número de píxeles (en el eje horizontal) que hay entre las imágenes de la posición de las estrellas en las dos fotos, cuando las observas en la pantalla. Puedes utilizar el programa para calcular p_L, el tamaño del objeto de calibración en número de píxeles en la pantalla.

Este cálculo del valor de d es un ejemplo de cómo medir la distancia a una estrella mediante paralaje.

Ahora vamos a usar la regla para medir la distancia d directamente y compararla con el valor calculado por paralaje. ¿Qué error hay en la medida?

Puedes repetir la actividad colocando la ‘estrella’ a diferentes distancias para ver si la precisión de las medidas por paralaje varían con la distancia (ver la sección ¿Qué precisión podemos esperar?

Fotografía de paralaje con un punto de referencia

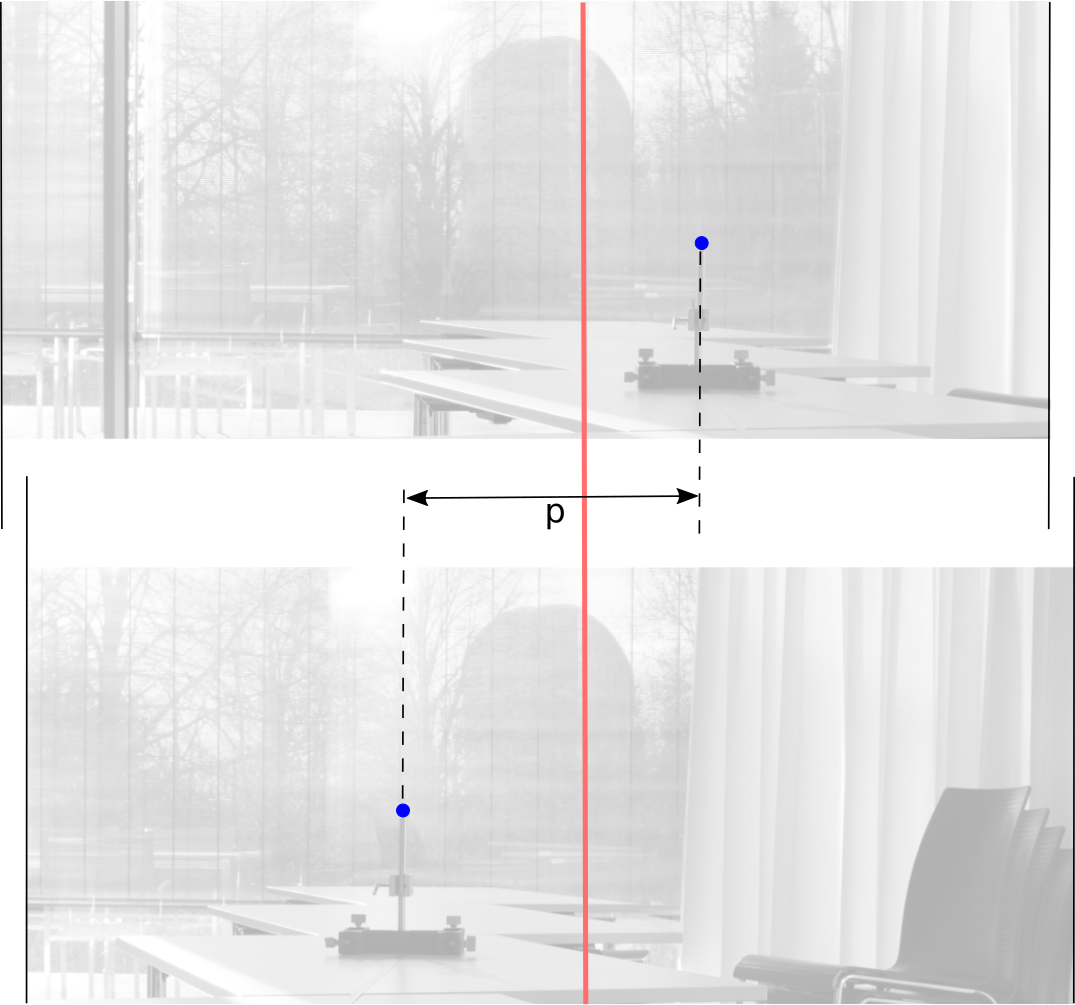
Para acercarnos más a la práctica real de los astrónomos podemos hacer una pequeña variación en el método y usar un objeto como referencia que esté fuera de la clase, que esté muy alejado de la ‘estrella’.  De esta manera vamos a buscar un objeto distante como referencia y que sea visible en las dos imágenes en lugar de apuntar con la cámara a la misma dirección después de desplazarla de A a B. Entonces mediremos en cada fotografía la distancia en píxeles desde la imagen de referencia al objeto. Este enfoque que se explica a continuación y que es ligeramente diferente, debería proporcionar  resultados más precisos.

Procedimiento

1. Busca alguna referencia pequeña lo más alejada posible y que aparezca en las dos imágenes. Tiene que estar mucho más alejado de lo que está la estrella modelo. En nuestro caso hemos elegido como referencia una de las cúpulas del Max Planck Institut für Astronomie que está a unos 80 m de la cámara.
    
2. En cada imagen, dibuja una línea vertical que pase por la referencia. Esta será la línea de referencia. Ahora podemos utilizar esta línea para encontrar la diferencia en píxeles entre las distancias de las dos imágenes, tal y como se muestra en la figura 4.
    

   

3. Para calcular la distancia p en la pantalla, medida en píxeles, necesitas primero conocer la distancia horizontal en píxeles desde la estrella modelo hasta la línea de referencia en cada una de las dos imágenes. Después, basta con sumar cada una de las dos distancias para calcular p.  Por ejemplo, -24px significa 24 píxeles a la izquierda de la línea de referencia, y + 36 px, 36 píxeles a la derecha, lo que hace que la distancia p sea de 60 píxeles.
    
4. Una vez conocido el valor de p, el resto de cálculos es el mismo que en el otro método (ver la sección ‘Calcular la distancia a la estrella’).

¿Qué precision podemos esperar?

¿Cuál es la precision de este método mejorado? Nuestros datos sugieren que las precisiones pueden ser muy precisas (si las comparamos con las medidas tomadas directamente), como se muestra en la figura 5. El valor máximo de error es del 3.2%.

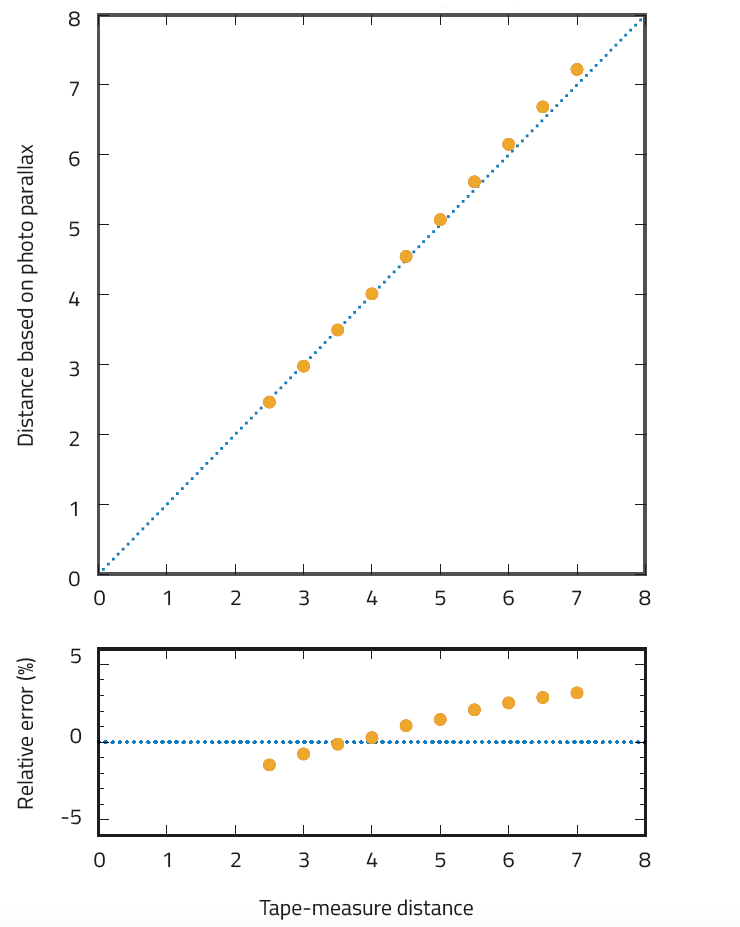
Observa que cuando aumenta la distancia también lo hace el error relativo y el error real. Esto sucede porque varía la geometría: la distancia a la estrella grande comparada con la distancia al objeto de referencia, por lo que el error obtenido por el método de la paralaje es mayor.

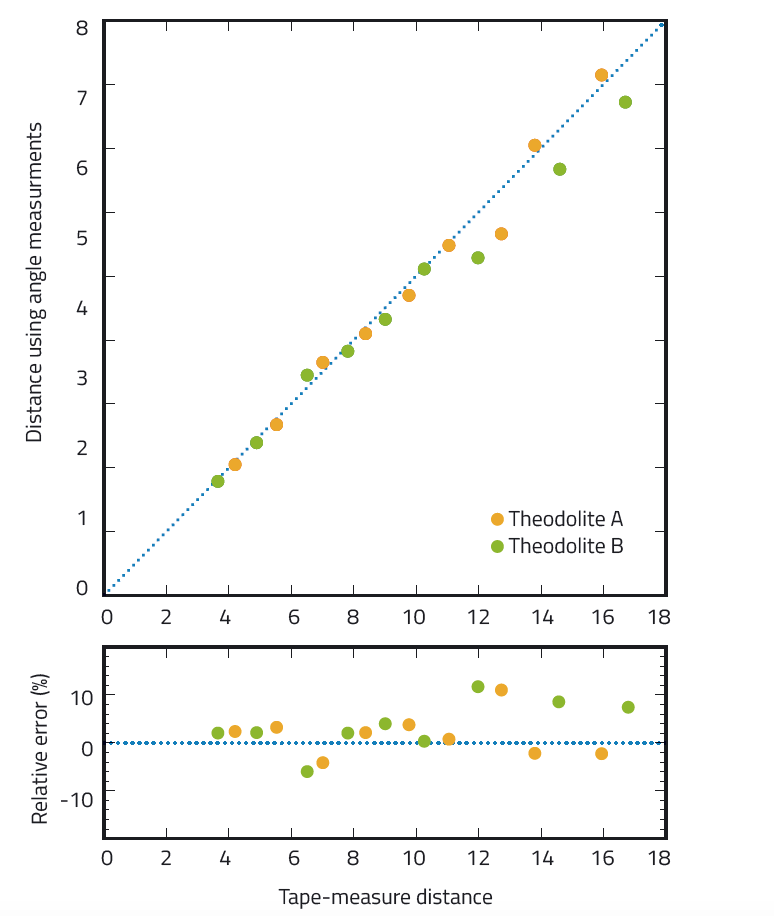
Con el método de medida de ángulos que se describió en un artículo anterior artículo (Pössel, 2017), la precisión de la distancia era significativamente menor –alrededor de un 10%, como se puede ver en la figura 6. Por eso este artículo ofrece una mejora significativa en la precisión sobre el método anterior, en el que la fuente principal de errores procedía de la medida de ángulos.