Supporting materials
Download
Download this article as a PDF

Μετάφραση από τη Σεβαστή Μαλάμου (Sevasti Malamou). Εξερευνώντας την οπτική οξύτητα απαιτεί όχι μόνο βιολογικά πειράματα, αλλά και κάποια κατανόηση της υποκείμενης…
Η οπτική οξύτητα είναι ένα μέτρο του πόσο οξεία είναι η όραση μας, ιδιαίτερα πόσο καλά μπορούμε να διακρίνουμε μικρές λεπτομέρειες. Οι οπτικοί το αξιολογούν ζητώντας από εμάς να διαβάσουμε από ένα διάγραμμα τοίχου μέχρι που τα γράμματα γίνονται πολύ μικρά για εμάς να τα διακρίνουμε με σαφήνεια.
Ένας από τους βιολογικούς παράγοντες που καθορίζουν την οπτική οξύτητα είναι η πυκνότητα των κυττάρων φωτοϋποδοχέων στον αμφιβληστροειδή χιτώνα (δείτε το κουτί, «Πως λειτουργούν τα μάτια μας»). Αυτό εγείρει μια ενδιαφέρουσα ερώτηση: θα μπορούσε η αύξηση της πυκνότητας των υποδοχέων στον αμφιβληστροειδή χιτώνα να κάνει πιο οξεία την όραση μας; Για να απαντήσουμε σε αυτό το ερώτημα, χρειάζεται να λάβουμε υπόψη τη βιολογία του οπτικού συστήματος και τη φυσική του φωτός. Αυτά τα ζητήματα είναι μέρος των περισσοτέρων προγραμμάτων σπουδών βιολογίας και φυσικής δευτεροβάθμιας εκπαίδευσης. Παρόλα αυτά, παραδοσιακά διδάσκονται ξεχωριστά, συχνά σε διαφορετικές ομάδες μαθητών. Σε αντίθεση, η διαθεματική προσέγγιση που προτείνεται εδώ θα επιτρέψει στους μαθητές να αποκτήσουν μια βαθύτερη κατανόηση τόσο της βιολογίας όσο και της φυσικής της οπτικής οξύτητας και θα μεταφέρει ένα σημαντικό γενικό μήνυμα: πολλά προβλήματα στη σύγχρονη επιστήμη μπορούν πολύ καλύτερα να επιλυθούν μέσω της ομαδικής εργασίας και της διεπιστημονικής συνεργασίας.
Αυτό το άρθρο περιγράφει έναν απλό τρόπο αξιολόγησης της οπτικής οξύτητας δημιουργώντας ένα διάγραμμα τοίχου και χρησιμοποιώντας το για τον υπολογισμό της ανάλυσης των ματιών. Αυτή η μέθοδος μπορεί να χρησιμοποιηθεί για την εκτίμηση της ελάχιστης απόστασης στον αμφιβληστροειδή χιτώνα στην οποία οι εικόνες δυο σημείων μπορούν να προσδιοριστούν ως δυο ευδιάκριτα ξεχωριστά αντικείμενα. Ένα πείραμα που ακολουθεί, που διατίθεται στο επιπλέον υλικό, συνδέει αυτή την απόσταση με τα θεωρητικά όρια της οπτικής οξύτητας με βάση τις φυσικές ιδιότητες του φωτός.
Οι δύο δραστηριότητες είναι οι πλέον κατάλληλες για μαθητές ηλικίας 16-19 ετών και θα διαρκέσουν περίπου δυο ώρες η κάθε μια, συμπεριλαμβανομένης της προετοιμασίας και της ανάλυσης των δεδομένων. Άλλες δύο ώρες χρειάζονται για τη συζήτηση των αποτελεσμάτων.
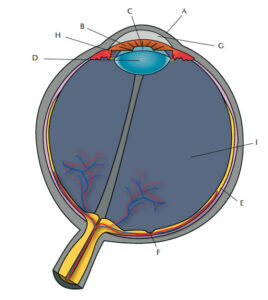
Ακτίνες φωτός που ανακλώνται από αντικείμενα εισέρχονται στο μάτι μέσω της κόρης. Τέσσερα μέρη του οφθαλμού- ο κερατοειδής, ο φακός, το υδατώδες υγρό και το υαλώδες υγρό- εστιάζουν τις ακτίνες του φωτός στον αμφιβληστροειδή χιτώνα, την επιφάνεια στο πίσω μέρος του βολβού του ματιού (σχήμα 1). Ο αμφιβληστροειδής χιτώνας είναι οργανωμένος σε διαφορετικά επίπεδα, ένα εκ των οποίων αποτελείται από εκατομμύρια φωτοϋποδοχείς που περνούν τα σήματα στων εγκέφαλο μέσω άλλων κυττάρων όπως τα γαγγλιονικά κύτταρα. Τα κύτταρα φωτοϋποδοχείς είναι εξειδικευμένα νευρικά κύτταρα και υπάρχουν δύο τύποι αυτών-τα ραβδία και τα κωνία (ονομάζονται έτσι εξαιτίας του σχήματος τους). Τα κωνία, βρίσκονται κυρίως στο κέντρο του αμφιβληστροειδούς χιτώνα, και επιτρέπουν την οξεία έγχρωμη όραση στο έντονο φως. Τα ραβδία, που βρίσκονται στην περιφέρεια του αμφιβληστροειδούς, μας βοηθούν να ανιχνεύσουμε την κίνηση και να δούμε σε αμυδρό φως, και επιτρέπουν την περιφερειακή όραση. Η πυκνότητα των φωτοϋποδοχέων στον αμφιβληστροειδή χιτώνα (η οποία μπορεί να είναι πάνω από 200000 κύτταρα ανά τετραγωνικό χιλιοστό στο κεντρικό βοθρίο) παίζει ένα σημαντικό ρόλο στην οπτική οξύτητα.
Η γωνιακή διακριτική ικανότητα του ανθρώπινου ματιού είναι ένα μέτρο της μικρότερης γωνίας μεταξύ δύο σημείων που γίνονται αντιληπτά ευδιάκριτα ως ξεχωριστά σημεία και σχετίζεται εν μέρει με την πυκνότητα των φωτοϋποδοχέων στον αμφιβληστροειδή χιτώνα. Είναι τυπικά περίπου 1 πρώτο λεπτό της μοίρας(το 1/60 της μοίρας). Σε αυτή τη δραστηριότητα, η γωνιακή ανάλυση υπολογίζεται με προσδιορισμό του λόγου της απόστασης μεταξύ των δύο σημείων και της απόστασης ανάμεσα στον παρατηρητή και τα δύο σημεία. Αυτή η απλοποιημένη μαθηματική διαδικασία (η οποία αντικαθιστά τον πιο πολύπλοκο υπολογισμό της εφαπτομένης της γωνίας α στο σχήμα 2) είναι δυνατή γιατί η γωνιακή ανάλυση αποκτά πολύ μικρές τιμές. Στα μαθηματικά, αυτή η προσέγγιση είναι γνωστή σαν η προσέγγιση μικρής γωνίας. Ο υπολογισμένος λόγος μπορεί στη συνέχεια να χρησιμοποιηθεί για την εκτίμηση της απόστασης αυτών των δύο σημείων που προβάλλονται πάνω στον αμφιβληστροειδή, όπως φαίνεται στο σχήμα 2.
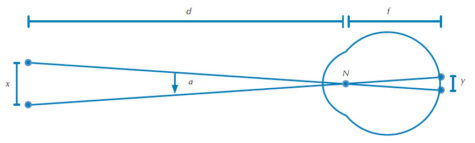
d= η απόσταση μεταξύ του αντικειμένου (στο πείραμα, το γράφημα τοίχου) και του οφθαλμού του εξεταζόμενου ατόμου, f= η εστιακή απόσταση του απλού οφθαλμού, x= η ελάχιστη αντιληπτή διαφορά μεταξύ δύο σημείων (στο πείραμα, το πλάτος της ελάχιστης αντιληπτής διαφοράς που χωρίζει δυο μαύρες ράβδους σε ένα διακεκομμένο μοτίβο ράβδων), y= η απόσταση μεταξύ των ειδώλων αυτών των δύο σημείων στον αμφιβληστροειδή, Ν= δεσμικό σημείο.
Η εικόνα είναι μια προσφορά του Günther KH Zupanc
Οι μαθητές θα κατασκευάσουν ένα διάγραμμα με απλές μαύρες γραμμές που διαχωρίζονται μεταξύ τους με κενά που ποικίλουν σε πλάτος. Στη συνέχεια θα τους ζητηθεί να δηλώσουν ποιες γραμμές θεωρούν ότι είναι ξεχωριστές και ποιες φαίνονται να έχουν συγχωνευθεί, και να χρησιμοποιήσουν αυτά τα αποτελέσματα για να υπολογίσουν μια εκτίμηση της γωνιακής ανάλυσης και έτσι την απόσταση των υποδοχέων στο μάτι.

Η γωνιακή ανάλυση του ανθρώπινου ματιού τυπικά ποικίλει μεταξύ 40 δεύτερων λεπτών της μοίρας και ενός πρώτου λεπτού της μοίρας. Για να αντιληφθείτε δυο ξεχωριστά σημεία, τουλάχιστον τρεις φωτοϋποδοχείς διατεταγμένοι σε ένα τόξο απαιτούνται: ένας να λάβει το φως από το κάθε σημείο και ένας για το κενό μεταξύ των σημείων. Για μια γωνιακή ανάλυση του 1 πρώτου λεπτού (το οποίο αντιστοιχεί σε 0,3 m σε μια απόσταση 1 Km), τα είδωλα στον αμφιβληστροειδή είναι χωρισμένα με μια απόσταση περίπου 6 μm, σημαίνοντας ότι η απόσταση ανάμεσα στα κέντρα δύο γειτονικών υποδοχέων είναι 3 μm. Σε μια γωνιακή ανάλυση των 40 δεύτερων λεπτών, η απόσταση μεταξύ των σημείων των ειδώλων είναι περίπου 4 μm.
Η πραγματική ανάλυση του οφθαλμού δεν επηρεάζεται μόνο από την απόσταση των φωτοϋποδοχέων, αλλά επίσης από τη διάθλαση του φωτός καθώς διέρχεται μέσα από την κόρη του οφθαλμού. Μπορείτε να το διερευνήσετε περαιτέρω κατεβάζοντας το πείραμα 2.
Έτσι, θα μπορούσε η οπτική οξύτητα να βελτιωθεί αυξάνοντας την πυκνότητα των κωνίων στον αμφιβληστροειδή;
Μια γωνιακή ανάλυση των 40 δεύτερων λεπτών ως 1 πρώτου λεπτού της μοίρας επιτυγχάνεται μόνο όταν κοιτάζουμε σταθερά προς ένα σημείο. Το είδωλο του αντικειμένου τότε προβάλλεται σε ένα συγκεκριμένο μέρος στο κέντρο του αμφιβληστροειδούς, το κεντρικό βοθρίο, το οποίο περιέχει μόνο φωτοϋποδοχείς κωνία. Η πυκνότητα των κωνίων στο βοθρίο είναι πολύ υψηλότερη από οπουδήποτε αλλού στον αμφιβληστροειδή, και τα κωνία εδώ έχουν διάμετρο μόνο 3 μm (συγκρινόμενα με την ως 10 μm διάμετρο στις άλλες περιοχές του αμφιβληστροειδούς). Επιτρέποντας κάποιον εξωκυτταρικό χώρο γύρω από κάθε κωνίο (π.χ. για τη μεταφορά θρεπτικών συστατικών), η απόσταση των κέντρων μεταξύ των κωνίων στο βοθρίο είναι περίπου 4 μm. Έτσι η πυκνότητα των κωνίων στο βοθρίο είναι ήδη πολύ κοντά στη μέγιστη δυνατή πυκνότητα τοποθέτησης.
Όπως μπορεί να διερευνηθεί στο επόμενο πείραμα, η περίθλαση του φωτός στον οφθαλμό ορίζει την ελάχιστη ευδιάκριτη απόσταση μεταξύ δύο σημείων φωτός να είναι περίπου 5 μm, δίνοντας μια ελάχιστη προβλεπόμενη απόσταση μεταξύ των κωνίων περίπου στα 2,5 μm. Επιτρέποντας κάποιον εξωκυττάριο χώρο μεταξύ των κωνίων, αυτή η θεωρητικά προβλεπόμενη απόσταση είναι σε πολύ καλή συμφωνία με την πραγματική απόσταση μεταξύ των κωνίων-υποδοχέων στο κεντρικό βοθρίο στα περίπου 4 μm. Ως εκ τούτου μια περαιτέρω αύξηση στην πυκνότητα των κωνίων δε θα μπορούσε να είναι εφικτή για βιολογικούς λόγους, και με βάση τους φυσικούς περιορισμούς που προσδιορίζονται από τις ιδιότητες του φωτός, δε θα οδηγούσε σε σημαντική αύξηση της οπτικής οξύτητας.
Αυτό το άρθρο περιγράφει δύο πειράματα που σχετίζονται με την οπτική οξύτητα, ένα παράδειγμα των πολυάριθμων συνδέσεων της βιολογίας με τη φυσική που μπορούν να βρεθούν στη φύση. Διαθεματικές δραστηριότητες μπορούν να κάνουν την επιστήμη πιο ελκυστική και μπορούν να προσφέρουν μια μεγάλη ευκαιρία για συνεργασία με άλλους εκπαιδευτικούς.
Όλα τα απαιτούμενα υλικά για τα πειράματα είναι εύκολα διαθέσιμα και οι οδηγίες είναι εύκολο να τις ακολουθήσει κανείς, κάνοντας τις δραστηριότητες κατάλληλες να εκτελεστούν από μαθητές σε μικρές ομάδες.
Το κείμενο θα μπορούσε να χρησιμοποιηθεί σαν ένα σημείο εκκίνησης για να συζητηθεί η σημασία της ομαδικής εργασίας και η διεπιστημονική συνεργασία για την επίλυση πολλών προβλημάτων στη σύγχρονη επιστήμη καθώς επίσης και σε άλλα θέματα.
Mireia Güell, Ισπανία
Download this article as a PDF