Ο νέος ορισμός για τους κρυστάλλους – ή πώς να κερδίσετε ένα βραβείο Νόμπελ Understand article
Μετάφραση από τον Λορέντζο Δημήτριο (Lorenzo Dimitrios). Γιατί η συμμετρία κατέχει κεντρικό ρόλο για την κατανόηση των κρυστάλλων; Και για ποιο λόγο η «απαγορευμένη»…

προσφορά της Schellhase;
Πηγή εικόνας: Wikimedia
Commons
Η μελέτη των κρυσταλλικών υλικών είναι μια από τις πιο ισχυρές αναλυτικές τεχνικές που είναι διαθέσιμες στους επιστήμονες. Αν είναι εφικτό να αναπτυχθεί ένας και μόνο κρύσταλλος άλατος, μορίου, πρωτεΐνης ή ακόμα και ενός ολόκληρου ιού, τότε συνήθως είναι δυνατό να αναγνωριστεί όχι μόνο η συνεκτικότητά του (ποια άτομα ενώνονται με ποια), αλλά και τα μήκη του δεσμού, οι γωνίες του δεσμού και η μοριακή διαμόρφωση (το σχήμα που υιοθετεί ένα εύκαμπτο μόριο). Από τη μελέτη κρυστάλλων πρωτεΐνης, είναι συχνά δυνατό να διευκρινιστεί με ποιο τρόπο αυτή λειτουργεί μέσα στο σώμα και σε ποιο σημείο βρίσκονται τα ενεργά κέντρα της.
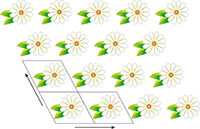
απεικονίζεται η μεταφορική
συμμετρία στις δύο
διαστάσεις. Τα
παραλληλόγραμμα
υποδεικνύουν την
επαναλαμβανόμενη
μονάδα Κάντε κλικ στην
εικόνα για μεγέθυνση
Η εικόνα είναι ευγενική
προσφορά της Mairi Haddow
Οι κρύσταλλοι είναι εκ γενετής εύμορφοι, χάρη κυρίως στη συμμετρία τους. Συμβατικά, όλοι οι κρύσταλλοι θεωρούταν ότι είχαν μια κοινή ιδιότητα: τη μεταφορική συμμετρία στις τρεις διαστάσεις. Πράγματι, με αυτό τον τρόπο είχαν αρχικά οριστεί οι κρύσταλλοι – ως υλικά στα οποία τα συστατικά άτομα, μόρια ή ιόντα είναι διατεταγμένα σε ένα τακτικό και επαναλαμβανόμενο μοτίβο στις τρεις διαστάσεις. Η μεταφορική συμμετρία απεικονίζεται ιδανικά στις δύο διαστάσεις αν φέρουμε στο μυαλό μας μια ταπετσαρία με σχέδια που έχει συνήθως την ιδιότητα αυτή – αν εφαρμοστεί κατάλληλα. Αυτό σημαίνει ότι μπορούμε να σχεδιάσουμε ένα παραλληλόγραμμο (πλακίδιο) (tile) που να περιέχει ένα συγκεκριμένο σχέδιο, και τοποθετώντας το σε δύο διευθύνσεις, να πάρουμε το σχέδιο της ταπετσαρίας (εικόνα 1).
Παρομοίως, μπορούμε να εξάγουμε μια τρισδιάστατη κρυσταλλική δομή από ένα “κουτί” ατόμων, το οποίο επαναλαμβάνεται κατά μήκος των αξόνων x, y, και z. Το επαναλαμβανόμενο κουτί είναι γνωστό ως μοναδιαία κυψελίδα (εικόνα 2).
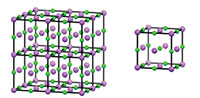
Κάντε κλικ στην εικόνα για μεγέθυνση
Η εικόνα είναι ευγενική προσφορά της Mairi Haddow

ατομική δομή των
ημιπεριοδικών κρυστάλλων
σε μια συνάντηση στο
Εθνικό Ινστιτούτο Προτύπων
και Τεχνολογίας (National
Institute of Standards and
Technology), στις ΗΠΑ, το
1985 – μερικούς μήνες μετά
τη δημοσιοποίηση της
ανακάλυψής του
Η εικόνα είναι ευγενική
προσφορά του Phillip
Westcott, National Institute of
Standards and Technology
Η συμμετρία στους κρυστάλλους και ημιπεριοδικότητα (quasi-periodicity)
Οι κρύσταλλοι που έχουν τέτοιου είδους μεταφορική συμμετρία στις τρεις διαστάσεις επισήμως αναφέρονται ως περιοδικοί κρύσταλλοι, γιατί οι δομές έχουν ένα μοτίβο που επαναλαμβάνεται σε ορισμένη απόσταση ή περίοδο. Το 2011, ωστόσο, το βραβείο Nobel στη Χημεία απονεμήθηκε στον Dan Shechtman για την ανακάλυψη των ημιπεριοδικών κρυστάλλων. Οι κρύσταλλοι αυτοί δεν είναι περιοδικοί – δεν διαθέτουν μεταφορική συμμετρία – όμως εμφανίζουν τοπική τάξη. Έχουν την ίδια επαναλαμβανόμενη μονάδα σε διαφορετικά σημεία στον κρύσταλλο, όχι όμως κατά περιοδικά διαστήματα. Η πρόσφατη αναγνώριση αυτής της εργασίας αποτελεί θρίαμβο για την επιμονή του Shechtmann μετά τη γελοιοποίηση που υπέστη όταν την πρωτοδημοσίευσε (Shechtman et al., 1984). Για ποιο λόγο όμως ήταν αυτή η ιδέα τόσο αμφισβητήσιμη; Για το λόγο ότι οι κρύσταλλοι αυτοί φαινόταν να έχουν συμμετρίες που απαγορεύονται στα περιοδικά συστήματα.
Εκτός από τη μεταφορική συμμετρία, οι περισσότερες περιοδικές κρυσταλλικές δομές έχουν και άλλη συμμετρία, όπως κατοπτρική συμμετρία. Για παράδειγμα, κοιτώντας τη μοναδιαία κυψελίδα του χλωριούχου νατρίου, βλέπουμε ότι το κάθε μισό είναι η κατοπτρική εικόνα του άλλου μισού (εικόνα 3; δείτε επίσης την εικόνα 4).
Η περιστροφική συμμετρία είναι επίσης δυνατή. Αυτό σημαίνει ότι αν περιστρέψουμε ένα αντικείμενο γύρω από ένα κεντρικό σημείο για ορισμένο αριθμό μοιρών, αυτό θα φαίνεται το ίδιο (εικόνα 4).
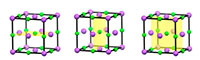
Κάντε κλικ στην εικόνα για μεγέθυνση
Η εικόνα είναι ευγενική προσφορά της Mairi Haddow

Κάντε κλικ στην εικόνα για μεγέθυνση
Εικόνα δημόσιας κυριότητας (σύμβολο ανακύκλωσης); Η εικόνα είναι ευγενική προσφορά της Mairi Haddow
Κάντε κλικ στην εικόνα για μεγέθυνση
Η εικόνα είναι ευγενική προσφορά της Mairi Haddow
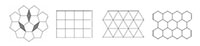
Όταν ένα σχέδιο ή ένας κρύσταλλος έχει μεταφορική συμμετρία και είναι περιοδικός, οι δεύτερης, τρίτης, τέταρτης και έκτης τάξης περιστροφικές συμμετρίες είναι όλες δυνατές, όμως οι πέμπτης, έβδομης ή και ανώτερης τάξης συμμετρίες, δεν είναι. Αυτό οφείλεται στο ότι τα τρίγωνα, τα ορθογώνια, τα τετράγωνα και τα εξάγωνα μπορούν να στοιβαχτούν σε ένα χώρο δύο διαστάσεων χωρίς να αφήσουν κάποιο κενό ανάμεσά τους. Αντίθετα, τα πεντάγωνα, τα επτάγωνα και τα ανώτερα πολύγωνα δεν μπορούν (εικόνα 5).
Με ποιο τρόπο αναλύονται οι κρύσταλλοι;
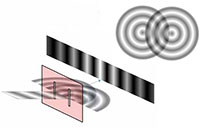
περίθλασης του Young, όπου
φαίνεται η συμβολή του
φωτός που διέρχεται από
ένα φράγμα περίθλασης.
Κάντε κλικ στην εικόνα για
μεγέθυνση
Η εικόνα είναι ευγενική
προσφορά της Mairi Haddow
Πολλοί μαθητές θα έχουν εκτελέσει στο σχολείο το διάσημο πείραμα διπλής σχισμής του Young, κατά το οποίο φως από laser πορεύεται μέσα από ένα φράγμα περίθλασης διαμέσω δύο σχισμών, των οποίων οι διαστάσεις είναι συγκρίσιμες με το μήκος κύματος του φωτός του laser. Μπορεί να φανεί η εικόνα συμβολής, που προκαλείται από την ενισχυτική και καταστροφική συμβολή των κυμάτων που περιθλώνται από τις σχισμές (εικόνα 6).
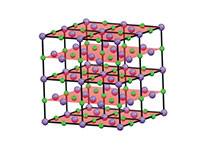
στο χλωριούχο νάτριο που
συμπεριφέρονται παρόμοια
με σχισμές σε ένα φράγμα
περίθλασης. Κάντε κλικ
στην εικόνα για μεγέθυνση
Η εικόνα είναι ευγενική
προσφορά της Mairi Haddow
Οι κρύσταλλοι μελετώνται με τη χρήση μιας τεχνικής που είναι γνωστή ως περίθλαση ακτίνων-Χ, η θεωρία της οποίας αναπτύχθηκε εκτενώς το 1913 από τον William Henry Bragg και τον υιό του William Lawrence Bragg, στους οποίους απονεμήθηκε από κοινού το βραβείο Νόμπελ στη Φυσική το 1915 για την εργασία τους. Σε ένα πείραμα περίθλασης, οι κρύσταλλοι συμπεριφέρονται ως ένα σύνθετο φράγμα περίθλασης, στο οποίο οι «σχισμές» είναι επίπεδα ατόμων μέσα στο κρύσταλλο (εικόνα 7).
Για να συμβεί περίθλαση, το μήκος κύματος της ακτινοβολίας που αλληλεπιδρά με τον κρύσταλλο πρέπει να είναι συγκρίσιμο με την απόσταση μεταξύ των ατόμων.
Συνήθως στα εργαστήρια, η ακτινοβολία θα είναι ακτίνες-Χ (που σκεδάζονται από τα ηλεκτρόνια των ατόμων), υπάρχουν ωστόσο και άλλες δυνατότητες, όπως ηλεκτρόνια ή νετρόνιαw1.
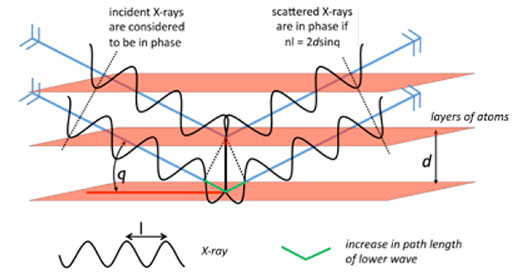
Ο κρύσταλλος στερεώνεται σε μια δέσμη ακτίνων-Χ με συγκεκριμένο μήκος κύματος, και η εικόνα περίθλασης λαμβάνεται όσο ο κρύσταλλος περιστρέφεται. Για επίπεδα ατόμων που είναι τοποθετημένα σε γωνία q ως προς τη δέσμη ακτίνων-Χ, οι σκεδαζόμενες ακτίνες-X θα βρίσκονται σε φάση (δηλαδή συμβαίνει ενισχυτική συμβολή) αν και μόνο αν η διαφορά μεταξύ των οπτικών δρόμων δύο σκεδαζόμενων ακτίνων-Χ είναι ίση με ένα ακέραιο αριθμό μηκών κύματος, και το αποτέλεσμα θα είναι ένα μετρήσιμο μέγιστο περίθλασης. Αυτό είναι γνωστό ως νόμος Bragg, και η εξαγωγή του απεικονίζεται στην εικόνα 8.
Η εικόνα είναι ευγενική προσφορά της Mairi Haddow

περίθλασης από ένα
συμβατικό κρύσταλλο σε
μια συγκεκριμένη γωνία. Το
κάθε λαμπερό σημείο
(ανάκλαση) αντιπροσωπεύει
ενισχυτική συμβολή από ένα
διαφορετικό επίπεδο
ατόμων. (Το σχήμα στα
δεξιά είναι η σκιά της
διάταξης διακοπής δέσμης,
μιας μεταλλικής θωράκισης
που απορροφά τη δέσμη
των ακτίνων-Χ που δεν έχει
σκεδαστεί)
Η εικόνα είναι ευγενική
προσφορά της Mairi Haddow
Όσο ο κρύσταλλος περιστρέφεται, διαφορετικά επίπεδα ατόμων θα ικανοποιούν το νόμο του Bragg και θα προκαλούν ενισχυτική συμβολή. Αυτό έχει σαν αποτέλεσμα ένα μέγιστο περίθλασης, του οποίου η ένταση σχετίζεται με τον αριθμό και το είδος των ατόμων στο επίπεδο, για παράδειγμα όπως φαίνεται στην εικόνα 9. Ένα τυπικό πείραμα περίθλασης καταγράφει χιλιάδες με εκατομμύρια ανακλάσεις, και με προσεκτική ανάλυση μπορεί να χρησιμοποιηθεί για να διαπιστωθεί η ακριβής δομή του κρυστάλλου.
Η εικόνα περίθλασης που παράγεται από ένα κρύσταλλο έχει και αυτή συμμετρία που σχετίζεται με τη συμμετρία του κρυστάλλου. Οι εικόνες περίθλασης των ημιπεριοδικών κρυστάλλων έχουν συμμετρία που είναι απαγορευμένη για τους περιοδικούς κρυστάλλους, όπως η πέμπτης ή δέκατης τάξης περιστροφή (εικόνα 10).
Οι δομές αυτών των ασυνήθιστων κρυστάλλων έχουν σχέση με τις πλακοστρώσεις Penrose (Penrose tilings) (εικόνα 11). Οι κατασκευές αυτές διαθέτουν τοπική συμμετρία, όχι όμως μεταφορική συμμετρία.

Οι εικόνες προσφέρθηκαν από την Mairi Haddow (οι εικόνες δεξιά και αριστερά); η κεντρική εικόνα προσφέρθηκε από τον Materialscientist; πηγή εικόνας: Wikimedia Commons

μπορεί να έχει περιστροφική
συμμετρία πέμπτης τάξης
(επάνω) όμως τέτοια
αντικείμενα δεν μπορούν να
συνδυαστούν σε ένα
περιοδικό σύστημα. Αυτό
συμβαίνει, για παράδειγμα,
στις πλακοστρώσεις Penrose
(κάτω), στις οποίες μπορούν
να βρεθούν περιοχές στις
οποίες υπάρχει τοπική
πενταπλή συμμετρία, χωρίς
όμως να υπάρχει
μεταφορική συμμετρία
Η εικόνα είναι ευγενική
προσφορά της Mairi Haddow
Έρευνα στον τομέα αυτό οδήγησε σε μια αλλαγή στον ορισμό ενός κρυστάλλου από τη Διεθνή Ένωση Κρυσταλλογραφίας (International Union of Crystallography) το 1991. Οι κρύσταλλοι πλέον δεν χρειάζεται να έχουν μεταφορική συμμετρία: ένα υλικό είναι κρύσταλλος αν έχει μια ευκρινή εικόνα περίθλασης, την οποία οι ημιπεριοδικοί κρύσταλλοι σίγουρα έχουν.
Ωστόσο, είναι απίθανο να αλλάξει σύντομα η σχολική διδακτική ύλη ώστε να περιλάβει αυτό τον νέο ορισμό. Ελάχιστα από αυτά τα ημιπεριοδικά υλικά έχουν ανακαλυφθεί, και ο πρώτος φυσικός ημιπεριοδικός κρύσταλλος – ο εικοσαεδρίτης (icosahedrite, Al63Cu24Fe13), ένα ορυκτό που πιθανόν έχει προέλευση από μετεωρίτη και βρέθηκε στον ποταμό Khatyrka στην Ανατολική Ρωσία – ανακαλύφθηκε μόλις το 2009 (Bindi L et al., 2009). Παρ’ όλο που έχουν αναπτυχθεί και άλλα παραδείγματα από τότε και είναι γνωστό ότι οι ημιπεριοδικοί κρύσταλλοι υπάρχουν σε πολλά μεταλλικά κράματα και σε ορισμένα πολυμερή, είναι απίθανο οι κρύσταλλοι που αναπτύσσουν οι μαθητές στο εργαστήριο να μην είναι περιοδικοί, επιπλέον πέρα από τις ασυνήθιστες και ενδιαφέρουσες ιδιότητές τους, οι ημιπεριοδικοί κρύσταλλοι δεν έχουν πραγματικές εφαρμογές – προς το παρόν.
References
- Bindi L et al. (2009) Natural Quasicrystals. Science 324(5932): 1306-1309. doi: 10.1126/science.1170827
- Shechtman D et al. (1984) Metallic phase with long-range orientational order and no translational symmetry. Physical Review Letters, 53(20): 1951-1953. doi: 10.1103/PhysRevLett.53.1951
Web References
- w1 – Η ανάλυση με περίθλαση δεν είναι δυνατή μόνο με ακτίνες-Χ, αλλά και με νετρόνια και ηλεκτρόνια. Χαρακτηριστικό παράδειγμα για αυτό αποτελούν τρία μέλη του EIROforum, που εκδίδει το Science in School.
-
Οι Ευρωπαικές Εγκαταστάσεις για την Ακτινοβολία Σύγχροτρον (European Synchrotron Radiation Facility) χρησιμοποιεί τις εικόνες περίθλασης από υψηλής ενέργειας ακτίνες-Χ για να αναλύσει υλικά. Τα πειράματα που εκτελούνται στο ESRF βρίσκουν εφαρμογή όχι μόνο στην επιστήμη των υλικών, αλλά και στη βιολογία, στην ιατρική, στη φυσική, στη χημεία, στην επιστήμη του περιβάλλοντος, ακόμα και στην παλαιοντολογία και στην πολιτιστική κληρονομιά.
-
Στο Ινστιτούτο Laue-Langevin λειτουργεί η πιο δυνατή σταθερή πηγή νετρονίων παγκοσμίως. Μελέτες περίθλασης των δεσμών νετρονίου χρησιμοποιούνται για την έρευνα στη φυσική συμπυκνωμένης ύλης, στη χημεία, στη βιολογία, στην πυρηνική φυσική και στην επιστήμη υλικών.
-
Το Ευρωπαικό Laser Ακτίνων-Χ Ελευθέρων Ηλεκτρονίων (European X-ray Free Electron Laser), που αναμένεται να λειτουργήσει μέσα στο 2015, θα κάνει χρήση αναλαμπών ακτίνων-Χ για την εξέταση δειγμάτων. Η βασική ιδέα ενός τυπικού πειράματος είναι απλή: φωτίστε ένα δείγμα με έντονες αναλαμπές ακτίνων-Χ και μετρήστε τα φωτόνια που διασπείρονται από το δείγμα σε διαφορετικές κατευθύνσεις. Το αποτέλεσμα είναι μια εικόνα περίθλασης.
-
Resources
- Cornuéjols D (2009) Biological crystals: at the interface between physics, chemistry and biology. Science in School 11: 70-76.
- Για να μάθετε πώς να φτιάξετε τους δικούς σας κρυστάλλους πρωτεΐνης, δείτε:
-
Blattmann B, Sticher P (2009) Φτιάξτε μόνοι σας κρυστάλλους πρωτεΐνης. Science in School 11.
-
- Περισσότερες πληροφορίες για τον Dan Shechtman και την ανακάλυψή του.
- Howes L (2011) Quasicrystals scoop prize. Chemistry World 8(11): 38-41.
- Για μια συνέντευξη με τον μαθηματικό και ερευνητή συμμετρίας Marcus de Sautoy, δείτε:
-
Hayes E (2012) Μαθηματικά εκεί που δεν το περιμένεις: συνέντευξη από τον Marcus du Sautoy. Science in School 23.
-
Review
Όπως γράφει ο συγγραφέας, «οι κρύσταλλοι είναι εκ γενετής εύμορφοι», παρ’όλα αυτά οι μαθητές συχνά βρίσκουν την κρυσταλλογραφία βαρετή και δύσκολη. Για τους μαθητές αυτούς και τους καθηγητές τους, το άρθρο της Mairi Haddow είναι μια πολύτιμη πηγή για να προσεγγίσουν τους κρυστάλλους με μια νέα ματιά και να εμπνευστούν από αυτούς. Σε αυτό το απολαυστικό άρθρο, το θέμα επεξηγείται με καθαρό και ακριβή τρόπο, συνδυάζοντας όμορφες και εντυπωσιακές εικόνες (για παράδειγμα εκείνη που αφορά την ταπετσαρία και την μεταφορική συμμετρία).
Το άρθρο θα μπορούσε να χρησιμοποιηθεί στα προγράμματα σπουδών της χημείας (δομές στερεών), φυσικής (περίθλαση, κύματα, ατομική δομή), επιστήμης της γης (ορυκτολογία, κρυσταλλογραφία), και των μαθηματικά (συμμετρία). Αυτά τα μαθήματα, με την προσθήκη της ιστορίας της τέχνης (πλακόστρωση) (tiling), προσφέρουν διαφορετικές διεπιστημονικές δυνατότητες.
Κατάλληλες ερωτήσεις κατανόησης περιλαμβάνουν:
- Από το άρθρο μπορεί να βγει το συμπέρασμα ότι είναι δυνατό να φτιάξει κανείς ένα κρύσταλλο:
- Ενός άλατος
- Ενός μορίου
- Ενός ιού
- Ενός βακτηρίου
- Με ποιο από τα παρακάτω ΔΕΝ μπορεί να πραγματοποιηθεί ανάλυση των κρυστάλλων με περίθλαση;
- Ακτίνες-Χ
- Ραδιοκύματα
- Νετρόνια
- Laser ελεύθερων ηλεκτρονίων
- Με ποιο από τα παρακάτω είδη πλακιδίων είναι δυνατό να καλυφθεί τελείως μια επιφάνεια δύο διαστάσεων;
- Τρίγωνα, τετράγωνα, πεντάγωνα, και εξάγωνα
- Τρίγωνα, ορθογώνια και επτάγωνα
- Τρίγωνα, τετράγωνα, ορθογώνια και εξάγωνα
- Τετράγωνα, ορθογώνια και πεντάγωνα
Giulia Realdon, Ιταλία





