Exploring radioactivity safely with potassium carbonate Teach article

Safety first: nuclear decay and ionizing radiation can be safely studied in the physics classroom using the common baking ingredient potassium carbonate.

Introduction

Teaching radioactivity in schools often involves challenges related to safety regulations, legal requirements, and cost. Traditional sealed radioactive sources – once a staple in physics classrooms – have become increasingly impractical due to strict regulatory demands, expensive storage and disposal protocols, and declining educational relevance. In Germany, for example, the Strahlenschutzverordnung (Radiation Protection Ordinance)^[1] sets stringent activity thresholds, making the use of these sources in schools both legally and logistically difficult.

This article presents an alternative approach: exploring the radioactive properties of potassium-40 using everyday materials like potassium carbonate (K₂CO₃), commonly known as potash. This compound is inexpensive, widely available, and it contains naturally occurring potassium-40 in quantities far below legal exemption limits.

By using this approach, students can investigate fundamental nuclear physics phenomena – such as beta and gamma radiation, absorption, and half-life – without the need for licensed radioactive sources. At the same time, the activity encourages scientific inquiry; promotes critical thinking; and helps demystify radiation by connecting it to familiar, real-world substances.

Introductory presentation

You can easily demonstrate the radiation of a food ingredient by holding small unopened paper bags containing 20 g of potassium baking additive directly in front of a sensitive 2-inch Geiger–Müller (G-M) tube, often called a G-M ‘pancake’ detector. Electrons and gamma photons easily pass through the paper envelope and the electrons will produce a signal of approximately 7–10 counts per second (cps), which is significantly higher than the background of approximately 0.5–1.0 cps without any specific source of radiation.

Note: this activity isn’t given in Bq because the detector doesn’t give you the activity of the sample unless you know the energy-dependent efficiency, the distance (geometry) shielding, and self-absorption of the probe.

20 g of potassium carbonate contains approximately 11.3 g potassium, which has a specific activity of approximately 31 Bq/g. The total activity in one small bag is approximately 360 Bq (89.3% beta minus, 10.7% electron capture plus gamma, 0.0% beta plus).^[2]

This produces approximately 320 fast electrons per second, with E_max = 1.31 MeV, which easily pass through paper and produce the counts. 34 gamma photons (E = 1.5 MeV) per second will seldomly contribute to your count, because the gamma response of the G-M tube is very low, but the photons are moving quite far. So do the approximately 320 electron antineutrinos per second (E_max = 1.3 MeV), which easily pass through your body, the building, and even through the Earth.

If you use two or three unopened small bags as a stack, the result will be only a very small increase in cps. This is because the beta particles from the second and third layers are absorbed by the sample itself before they can reach the detector. This effect is called self-absorption.

If you use a bigger sample of potassium salt, you will only get beta particles from the outer layer with a thickness of approximately 2.0–5.0 mm.^[3]

You can find more information in the radioactivity infosheet in the supporting material, which can also be used as a handout for students during the activities.

Activity 1: Absorption experiments

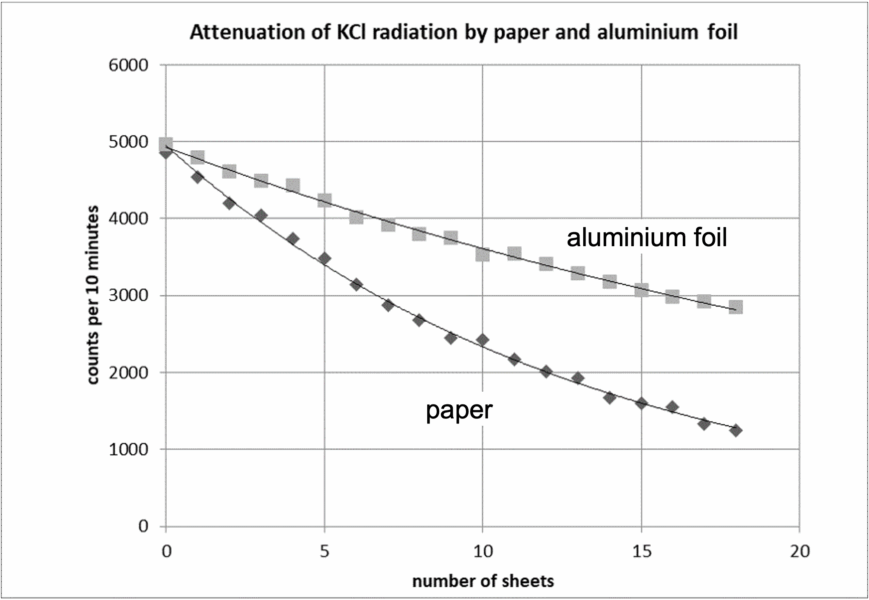
This activity introduces students to the attenuation of beta radiation by different materials. Using potassium carbonate, which is a radiation source, students investigate how the intensity of detected radiation decreases when it passes through shielding materials.

The activity takes 45–60 minutes (which can be split over two lessons).

Materials

• 1–2 kg potassium carbonate (K₂CO₃). It is used as a drying agent and in the food industry and you can find various providers online. An alternative is potassium chloride (KCl), which is used as a fertilizer and as a salt substitute in food.
• G-M pancake detector
• Small flat containers like Petri dishes with a diameter of 90 mm or more
• Absorber materials: aluminium foil, plexiglass, paper, and lead sheets
• Ruler or caliper (to measure thickness)
• Stopwatch or timer
• Support stand for consistent geometry
• Optional: computer with spreadsheet software for data analysis

Procedure

1. Place a known mass of potassium carbonate or potassium chloride in a flat container. Position the detector directly above it at a fixed distance (e.g., 10 cm).
2. Record background radiation for 10 minutes without any source.
3. Place the potassium carbonate under the detector and record the radiation for 10 minutes (or longer for more accurate data).
4. Repeat the measurement with a sheet of paper between the source and detector as an absorber.
5. Then try increasing the absorber thickness (i.e., multiple sheets of paper). Record the count rate after each addition.
6. Compare different absorber materials (paper, aluminium foil, lead sheets), noting the thickness each time. Ideally, also try to compare different materials at the same thickness, using multiple sheets of thinner materials to achieve this.
7. Ask students to reflect on the results using guiding questions:
   – Why does the count rate drop with each added layer?
   – What kind of radiation might still be detected through aluminium or lead?
   – Why is it that paper absorbs more beta particles than aluminium foil?

Results/discussion

The observed decrease in count rate reflects the absorption of beta radiation. Paper and thin aluminium block most beta particles.

Activity 2: Range and distance law

This activity explores how the intensity of detected radiation depends on the distance from the source by investigating the range of beta particles in air. This experiment supports discussions on radiation type, range, and fundamental laws like geometric dilution.

This activity takes about 45 minutes.

Materials

• 1–2 kg potassium carbonate or potassium chloride
• G-M pancake tube
• Ruler or measuring tape
• Support stand with adjustable height
• Graph paper or spreadsheet software

Procedure

1. Place the potassium carbonate in a stable container on the lab bench.
2. Position the detector at a known distance (e.g., 2 cm) above the material.
3. Record the count for a fixed time interval (e.g., 5 or 10 min).
4. Increase the distance between detector and source in regular steps (e.g., 2 cm, 5 cm, 10 cm) and repeat the measurement at each distance.
5. Repeat the measurements with thin aluminium-foil shielding.
6. Have students plot the count versus distance.
7. Ask students the following questions:
   – What trend do you observe?
   – How does the count rate relate to distance?
   – What kind of radiation is most affected by increasing distance?

Results/discussion

Count rates plotted against distance typically show a sharp initial drop (mainly due to beta absorption in air). At close distances (≤1 cm), beta particles contribute significantly to the count rate. As the distance increases, beta particles are largely absorbed by air.

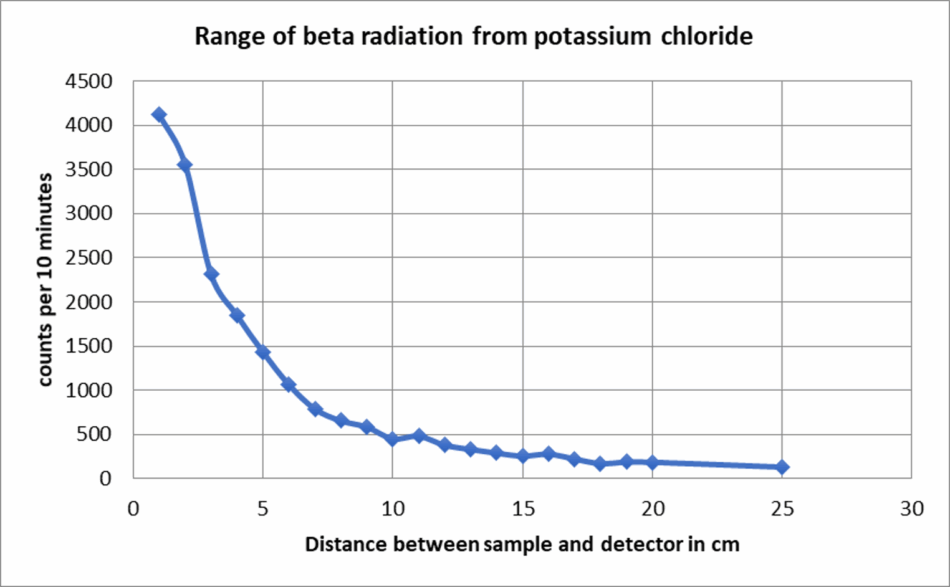
As an extension, students can plot the overlaying theory curve for gamma radiation: I ∝ 1/r  ².

Efficiency and limitations

• The beta range is limited by air absorption and geometry (a few mm in solids, several cm in air).
• G-M tubes may have different sensitivities, depending on window type.
• Gamma rays have a longer range and their intensity decreases approximately according to the inverse square law. But you will get very few counts from gamma rays due to the very low response of the detector to gamma photons (see the radioactivity infosheet).
• Background radiation must be subtracted carefully, especially at larger distances.

Activity 3: Gamma attenuation (Lambert–Beer law)

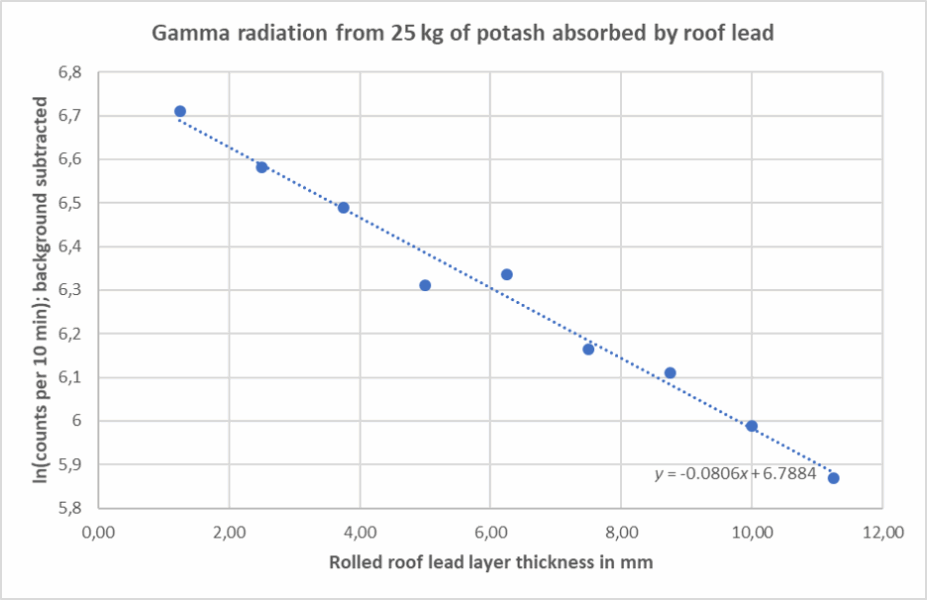
This activity demonstrates the exponential attenuation of gamma radiation as it passes through absorbing materials, such as lead. Students observe how gamma-ray intensity decreases with increasing shielding thickness and evaluate the absorption coefficient for high-energy gamma photons. This is a good opportunity to teach about exponential laws in physics and data analysis skills.

The activity takes about 45 minutes.

Materials

• 25 kg bag potassium carbonate for higher gamma-emission rates. If your school has a swimming pool, they may already have supplies of this for controlling the pH of the water.
• G-M pancake detector
• Plexiglas (PMMA) or polystyrene sheet of 1–2 cm thick to absorb beta radiation
• Lead and aluminium sheets of various thicknesses (e.g., lead: 1–12 mm total, Al 5–50 mm total)
• Ruler or micrometre
• Stopwatch
• Optional: spreadsheet or fitting software

Procedure

1. Put the 25 kg bag horizontally on a table or on the floor.
2. Leave the potassium carbonate in the bag and position the detector on top of it.
3. Record the count over a standard interval without any shielding.
4. Record the count over a standard interval using plastic shielding (baseline value).
5. Add lead sheets incrementally between the source and detector (e.g., in 1 mm intervals).

6. Measure and record the count rate for each lead thickness.
7. Repeat the measurement using aluminium sheets (e.g., in 5 mm steps).
8. Have students plot count rate versus lead thickness and then make a logarithmic plot (ln of the count rate versus lead thickness).
9. Ask students the following questions:
   – What pattern do you see in the measured values?
   – Is the rate dropping linearly or in another way?
   – Why does gamma radiation still penetrate even thick layers of lead?
10. Optional extension: have students calculate μ based on exponential attenuation and compare the results with reported values.

Results/discussion

Example data:

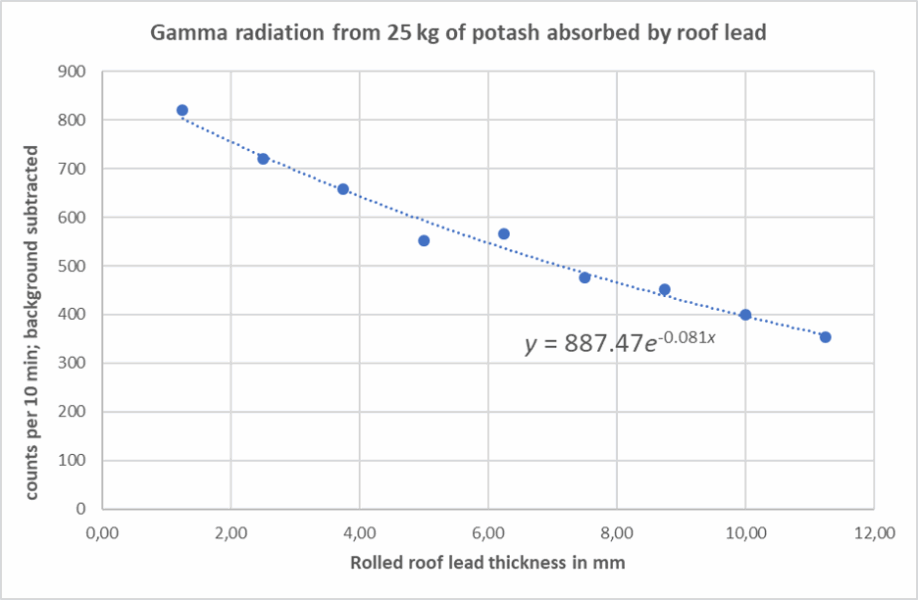
The logarithmic plot (ln I versus x) should yield a straight line:

Exponential attenuation

Gamma radiation is attenuated as it passes through matter according to the Beer–Lambert law:

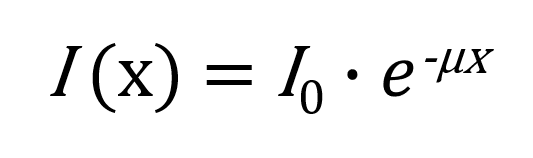
The value I (x ) gives the intensity after thickness x, and μ is the linear attenuation coefficient. The experimental data fits this law with μ ≈ 0.08 mm⁻¹ for lead. This allows us to calculate the half-thickness value:

Or the attenuation length:

These values agree with known data.^[4]

Efficiency and limitations

• Statistical fluctuations increase with higher shielding (lower count rates).
• For accurate results, long counting times are advised.
• Detector geometry must remain constant throughout.

Extension activity: Determination of half-life

Older students that already having some knowledge of radioactivity can estimate the half-life of potassium-40 based on measured count rates and known quantities of material. This activity introduces concepts such as specific activity, decay constants, and long-lived isotopes.

Full instructions for the determination of half-life activity can be found in the supporting material.

Conclusion

This series of experiments demonstrates that the core principles of radiation physics can be effectively taught using safe, accessible, and inexpensive materials. By using potassium carbonate – a simple food-grade compound rich in naturally occurring potassium-40 – students gain hands-on experience with beta and gamma radiation, shielding effects, the inverse square law, and the concept of half-life.

This model highlights that meaningful engagement with nuclear physics is not limited to specialized laboratories. With creativity and careful design, powerful learning experiences can be created using everyday materials – bringing radioactivity out of the shadows and into the light for student exploration.

---

Supporting materials

Radioactivity infosheet

Determination of half-life

Download

Download this article as a PDF

---

Share this article

• twitter
• facebook
• linkedin

---

Subscribe to our newsletter

Subscribe to our newsletter

Subscribe