Can something accelerate upwards while falling down? Teach article
Use one of the most surprising experiments in classical mechanics to teach the scientific method, video analysis and mechanics.
Classical mechanics in secondary education can sometimes be challenging to teach and to learn. Most experiments involve things like pulling a wooden block along a flat surface with a Newton meter or spring scale, or dropping a tennis ball from different heights – activities that may neither surprise nor engage the students to any desired extent. But thanks to the fast evolution of mobile phone cameras, video analysis can now be used to easily carry out investigations that a few years ago could be done only in top research labs. And detailed analysis of seemingly everyday phenomena can sometimes lead to the most surprising results!
This suggestion for a lesson activity is the result of such an investigation performed by a student for an ordinary physics course assignment, in which the results completely surprised both the student and the teacher.
The experiment

Norrby
A Slinky® is essential in any physics classroom. It can be used for many things, from illustrating longitudinal waves to walking down stairs. A Slinky has a surprising yet relatively well known property: if it is held by its top and stretched under its own weight, when released, the bottom of the Slinky will not move until the Slinky has collapsed completely (see figure 1). Many popular videos online show this interesting factw1.
The process is usually too fast to see with the naked eye, but it is clearly felt if one places a hand just underneath the bottom of the stretched Slinky before releasing it. You can easily demonstrate this peculiar property in the classroom, preferably by letting all students test it themselves by holding a Slinky with one hand and dropping it onto their other hand.

under its own weight and
then released
Image courtesy of Markus
Norrby
After introducing the phenomenon, you can pose a research question: Since the acceleration of the bottom part of the Slinky is zero, what is the acceleration of the top part of the Slinky during the fall?
The next step, according to the scientific method, would be to make a hypothesis. This could be discussed in the classroom. If the desired end product is a group or individual laboratory report, the hypothesis should be motivated by logical reasoning and possible references to literature and should be written down. In many cases, the hypothesis will be that the acceleration of the top part of the Slinky should be around 2g or higher, to give an average acceleration of g for the whole Slinky (at least that was our hypothesis when first conducting this investigation).
To answer the research question, video analysis should be used. For a detailed analysis, the Slinky drop needs to be filmed at a higher than normal frame rate, at least 60 frames per second but preferably 120 frames per second, which can be achieved by many newer smartphones. To reduce uncertainties, the students need to spend some time evaluating the errors that might affect the results of video analysis, such as filming angle, position of an object of known size for reference, and the resolution and shutter speed of the camera. A model procedure is outlined below.
Materials
Each student or group of students will need:
- Slinky
- Metre rule
- Tripod
- Video recording device (video camera or smartphone)
- Video analysis software (a great free tool is Trackerw2, a video analysis and modelling tool built on the Open Source Physics Java framework. We used Pasco Capstonew3, a commercial data acquisition and analysis tool. There are also apps available to perform the analysis directly on mobile devicesw4)
Procedure
- Attach the metre rule vertically to a wall, with the start of the rule (e.g. 0 cm end) at the top.
- Set up the tripod and camera so that the Slinky’s entire fall can be recorded.
- Hold the Slinky fully extended and align its top with the start of the metre rule.
- Start filming.
- Release the Slinky.
- Stop filming.
- If needed, import the video into the relevant analysis software.
- The exact procedure for tracking the object of interest in the video varies slightly between different types of video analysis software. The students should process the video to produce data that can be plotted in graphs showing time against speed, time against velocity or time against acceleration.
- Analyse results.
Since acceleration is the quantity of interest in this case, students will usually start by looking at the graph showing time against acceleration. However, they will find that their values are all over the place. This is a good learning opportunity to help the students understand why physics teachers keep nagging them about the line of best fit in different diagrams.
If the students then analyse a graph showing time against speed or time against velocity, they will see a much smoother curve and can obtain better results (see figures 2 and 3).
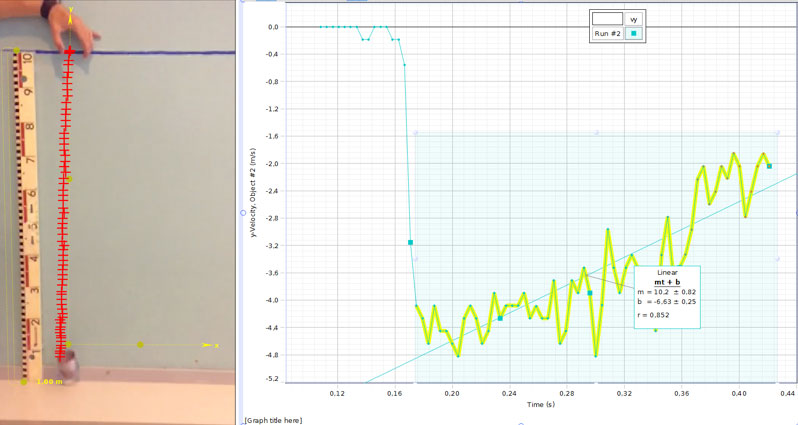
Image courtesy of Markus Norrby
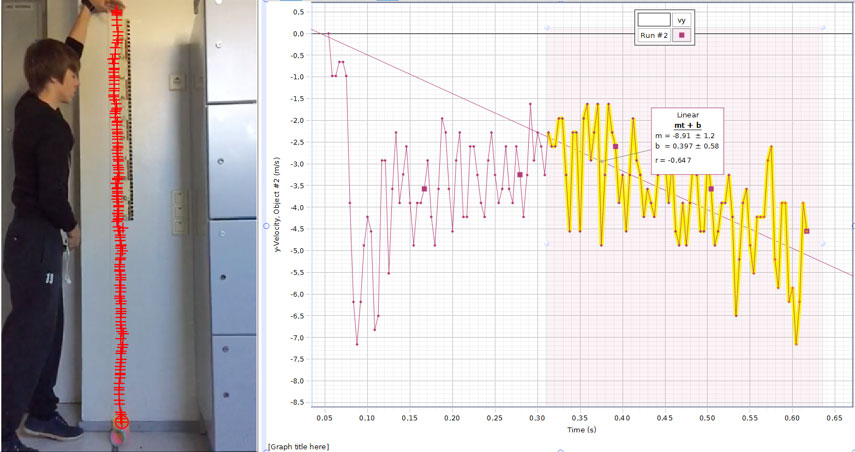
Image courtesy of Markus Norrby
About what happens
The original research question posed when first performing the experiment is how the acceleration of the top and the bottom of the Slinky relate to each other. Our first surprise after watching the slow-motion video was that the only part of the Slinky moving is the top. Each section of the Slinky below the top behaves just like the bottom part, hanging in the air (almost) until hit by the top.
The second, and even bigger surprise, came from the analysis of the acceleration of the top part. It turns out that the top of the Slinky has a huge acceleration in the first few milliseconds of being dropped – usually around 200–300 m s-2 on average. After that, the velocity abruptly decreases, with a seemingly constant value for the acceleration of about 10 m s-2. In fact, having repeated the experiment many times, and including Slinkies of different materials and diameters (see figure 4), the error bars of the results always include the value 9.8 m s-2, and the average comes very close to that of a negative acceleration of gravity.

tested by the authors
Image courtesy of Markus
Norrby
A simple way to convince oneself of the validity of the result is to continue the analysis a bit further after the Slinky has collapsed completely but before it hits the ground. The acceleration of the collapsed Slinky is, as expected, equal to the acceleration of gravity. By observing the symmetrical shape of the plot of time against velocity, it is clear that the sign of the acceleration changes during the Slinky’s fall, but that the modulus of the value remains much the same (figure 3). Figure 3 also shows that the total average acceleration for the whole motion is 9.8 m s-2, as we would expect.
These results should be discussed in the classroom. The students need to understand that there is no simple explanation for this behaviour; even the simplest models of the phenomenon include differential equations and propagating waves. The uncertainties of the results must be stressed, and professional equipment together with in-depth analysis would show additional structure in the behaviour, as with most real-life phenomena.
The problem of the falling Slinky has recently been investigated in more detail, and over the past few years more and more academic references turn up when you search the Internet for information on the subject. The explanation for the bottom part hanging in the air until the Slinky has collapsed is straightforward: information about the top of the Slinky being released travels as a wave through the Slinky and takes a certain amount of time to reach the bottom. But other aspects are more challenging to explain.
The phenomenon was investigated by Cross and Wheatland (2012), who made a semi-empirical model for the falling Slinky, assuming a finite collapse time of the turns behind a downward propagating wave and comparing to footage from a high-speed camera.
Their more detailed analysis agrees with the results that the students will find above, but the authors also observe a small oscillation in the acceleration during the fall. Their model, which predicts a non-constant deceleration, could not be conclusively proved. In Cross and Wheatland’s article, the data clearly imply an average acceleration for the negative acceleration phase of about 10 m s-2 but that is not mentioned in the article and not directly supported by the model.
Other researchers have tried different approachesw5 for modelling the falling Slinky but so far no single model seems to be able to explain fully the details of this complicated motion. So, as the saying goes: “More research is needed.” And while we wait for physics theory to catch up, we can use this fascinating experiment as inspiration for physics students around Europe.
There is an opportunity here for teachers to make the connection between this experiment and many historical experiments in which the outcome was completely unexpected. It is often these unforeseen results that can cause science to take a leap forward, such as Rutherford’s discovery of the atomic nucleus or Bequerel’s discovery of radioactivity.
References
- Cross RC, Wheatland M S (2012) Modeling a falling slinky. American Journal of Physics 80, 1051. doi: 10.1119/1.4750489. A preprint is freely available on ArXiv at http://arxiv.org/pdf/1208.4629.pdf
Web References
- w1 – Watch a slow-motion video of a Slinky falling, which also discusses some of the science involved.
- w2 – Download and find out more about the free image processing software Tracker.
- w3 – Download the commercial software the authors used, Pasco Capstone.
- w4 – One example of a video analysis app is Video Physics for iOS.
- w5 – Phil Gash, a professor of physics at California State University, has proposed an alternative model for a falling Slinky.
Review
As high-speed cameras and video analysis tools are becoming increasingly available, physics classrooms and laboratories can contribute new perspectives in the investigation of many types of motion. The study of fast moving or changing objects may reveal very interesting and fascinating aspects.
The Slinky (a pre-compressed helical steel or plastic spring) was invented as a toy. In this article, a student’s study of the motion and behaviour of a falling Slinky, brings unexpected and surprising results to light. Further inquiry and study of the fascinating behaviour of the Slinky can be continued in more classrooms and labs. And many more phenomena could be investigated by students using video analysis!
Vangelis Koltsakis, Greece





