Fundamente pentru ora de clasă: măsurarea constantei lui Planck Teach article
Tradus de Mircea Băduţ. Aducem descoperirea ştiinţifică în ora de clasă şi arătăm elevilor cum să evalueze constanta lui Planck folosind echipamente de laborator simple.

Imagine din domeniul public
/Wikimedia
Când ne gândim la evaluarea unor constante fizice fundamentale, precum viteza luminii sau forţa de gravitaţie, probabil că ne imaginăm experimente faimoase şi de scară mare – dar şi echipamentul de laborator şcolar ne poate ajuta să calculăm aceste valori statornice.
Constanta lui Planck poate părea mai degrabă un concept eteric, spre deosebire de – să zicem – viteza luminii, dar ea joacă un rol absolut central în înţelegerea comportamentului materiei la nivel subatomic. El este piatra de temelie a teoriei mecanicii cuantice, care descrie straniul comportament al particulelor la acest nivel. Aici energia, la fel ca materia, se constituie din particule. De exemplu, lumina, ca radiaţie electromagneticăw1, este constituită din particule numite fotoni.
Imagine din domeniul public/
Wikimedia
Numită după fizicianul german Max Karl Planck (1858–1947), constanta lui Planck ne spune că energia fotonilor individuali depinde de lungimea de undă a radiaţiei lor, după cum arată şi ecuaţia fundamentală:
Ep = hc/λ
unde Ep este energia fotonului (în joules) h este constanta lui Planck, c este viteza luminii în vid, iar λ este lungimea de undă a radiaţiei.
Deşi valoarea constantei lui Planck este exstraordinar de mică, am realizat o metodă de a o determina printr-un experiment de laborator de fizică. Surprinzător, activitatea nu necesită echipamente speciale – doar câteva diode electro-luminescente (LED) şi aparatură electrică standard. Această lecţie de laborator este potrivită pentru mulţi elevi şi studenţi, cu vârste de peste 16 ani.
Cum lucrează LED-urile
LED-urile sunt produse prin joncţiunea dintre două materiale semiconductoare dopate, dintre care unul are un exces de electroni (materialul de tip ‘n’) iar celălalt are lipsă de electroni, lipsurile fiind numite goluri (materialul de tip ‘p’). Când un curent electric este injectat prin această aşa-numită joncţiune ‘p-n’, recombinarea electronilor şi a golurilor determină eliberarea de energie sub formă de fotoni (emisia de lumină, deci).
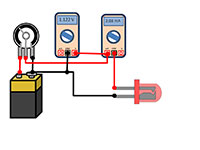
măsurarea răspunsului
tensiune-curent al fiecărui
LED. De la stânga la dreapta:
bateria, potenţiometrul sau
reostatul, voltmetrul,
ampermetrul, LED-ul.
Gratitudine pentru imagine:
autorii articolului
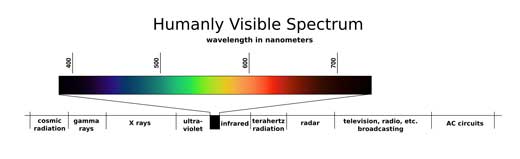
Culoarea luminii emise de un LED este dată de energia fotonilor, care poate fi controlată prin modificarea compoziţiei chimice a materialelor semiconductoare. LED-urile sunt de obicei confecţionate din aliaje de galiu, arseniu şi aluminiu, iar modificarea proporţiilor acestor constituenţi poate determina LED-urile să emită diverse culori – precum roşu şi verde în domeniul vizibil al spectrului electromagnetic –, sau să emită o lumină în regiunile ultraviolet ori infraroşu.
Ca în cazul oricărei lumini, lungimea de undă este cea care determină culoarea. Ochiul uman este sensibil la lumini cu lungimi de undă între 390 şi 700 nanometrii (0.00039–0.0007 mm). Noi vedem cele mai scurte lungimi de undă ca violet, iar pe cele mai lungi ca roşu, iar fiecare dintre lungimile de undă din interiorul acestui interval corespunde unei anumite culori din spectrul vizibil. De exemplu, LED-urile verzi produc de obicei lumină cu lungimea de undă de aproximativ 567 nanometri.
Folosim LED-uri în acest experiment deoarece fiecare culoare emisă are o tensiune de prag la care electronii încep să producă lumină. Măsurarea acestei tensiuni limită (tensiunea de deschidere), împreună cu valorile cunoscute pentru lungimile de undă emise, ne furnizează o metodă de a afla valoarea constantei lui Planck.
Materiale
- Patru LED-uri emiţând lumină colorată – unul pentru roşu, unul portocaliu, unui verde şi unul albastru. Alegeţi LED-uri cu o carcasă curată, necolorată, astfel încât culoarea luminii emise să fie dată doar de joncţiunea semiconductorilor şi nu de către învelişul acesteia.
- o baterie de 9 V.
- Două multimetre (unul pentru a fi folosit ca voltmetru iar celălalt ca ampermetru).
- Un potenţiometru (reostat) de 1 kΩ.
Procedura
- Alcătuiţi circutul electric ca în figura de mai sus. Conectaţi ampermetrul în serie cu LED-ul pentru a măsura curentul care trece prin el, şi conectaţi voltmetrul în paralel cu LED-ul pentru a măsura tensiunea la bornele acestuia. Tensiunea aplicată poate fi modificată prin acţionarea potenţiometrului (sau a reostatului).
- Creşteţi tensiunea în paşi de 0,05V de la 0 la 3 V, şi măsuraţi curentul electric rezultat. Notaţi rezultatele observate. De reţinut că atunci când curentul ce trece prin LED este mic, e posibil ca acesta să nu lumineze. Pentru a proteja LED-ul, urmăriţi să nu depăşiţi un curent de 5mA.
- Pentru fiecare LED, desenaţi graficul curentului în funcţie de tensiune, similar celui din figura alăturată. Pe fiecare grafic identificaţi linia dreaptă care se potriveşte cel mai bine cu punctele graficului ce se desprinde crescător de axa X. Dacă punctele se menţin aproape de această linie, înseamnă că în această regiune a graficului avem o relaţie liniară stabilă între tensiunea aplicată şi curent.
- În final, determinaţi tensiunea de activare (Va) a LED-urilor din datele colectate. Aceasta corespunde punctului în care curentul începe să crească liniar cu tensiunea. Punctul poate fi determinat din grafic prin extinderea liniei drepte (linie reprezentând regiunea răspunsului liniar) până la intersecţia cu axa X. Elevii pot face această extindere folosind o riglă, sau prin extrapolare matematică (aplicând o regresie liniară a datelor experimentale din regiunea liniar-crescătoare)w2.
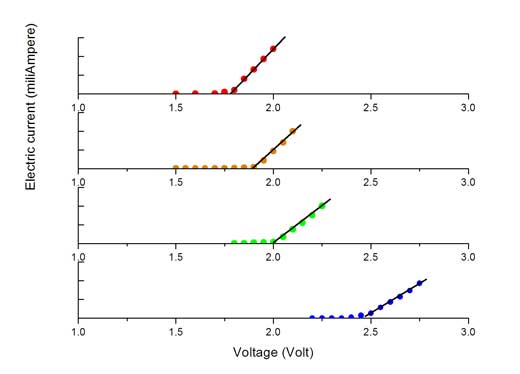
Pentru imagine mulţumim autorilor.
Pentru a obţine cele mai precise valori pentru Va fpentru fiecare culoare emisă de LED-uri, puteţi calcula o valoare medie folosind rezultate obţinute de mai mulţi elevi.
Valorile tipice ale tensiunii de activare obţinute prin acest experiment sunt prezentate în dreapta, împreună cu valorile lungimilor de undă pentru luminile emise de LED-uri. Puteţi furniza elevilor aceste valori ale lungimilor de undă pentru faza următoare a experimentului de laborator. De asemenea, lungimile de undă ar putea fi măsurate folosind un spectrometru atrizanal, precum cel descris în resursa web de mai josw3.
| Culoarea LED-ului | Lungimea de undă tipiă, λ (cm) | Tensiunea de activare/deschidere, Va (V) |
|---|---|---|
| Roşu | 623 | 1.78 |
| Portocaliu | 586 | 1.90 |
| Verde | 567 | 2.00 |
| Albastru | 567 | 2.45 |
Gratitudine pentru imagine: entirelysubjective/Flickr
Analiză şi rezultate
Aşa cum am văzut anterior, energia fotonilor emişi, Ep (măsurată în joules), este legată de constana lui Planck (h), de viteza luminii în vid (c), şi de lungimea de undă a luminii λ:
Ep = hc/λ(1)
În acest experiment, avem o mulţime de valori pentru lungimi de undă cunoscute ale culorilor LED-urilor, şi cunoaştem valoarea pentru c (2.9979 x 108 ms-1). Dar cum vom folosi valorile experimentale Va pentru a calcula constanta lui Planck? Pentru a afla, hai să intrăm un pic în intimitatea LED-ului!
Când LED-ul este alimentat cu tensiune scăzută, energia aplicată nu este suficientă pentru a produce fotoni, iar curentul electric este foarte slab. Dar la o anumită tensiune, LED-ul începe să emită fotoni: aceasta este tensiunea de activare, Va. Acest prag minim de tensiune pentru fiecare culoare de LED se corelează cu energia fotonilor emişi, Ep (ecuaţia 2). Astfel că, asemeni lui Ep, şi tensiunea Va este matematic dependentă de constanta lui Planck şi de lungimea de undă a luminii emise, conform ecuaţiei de mai jos:
Va = Ep/e + φ/c(2)
Aici e este sarcina electrică a electronului(1.6022 x 10−19 coulombi). Pentru tensiuni mai mari decât Va curentul electric este determinat de rezistenţa internă a LED-ului. Din legea lui Ohm (tensiunea = curentul x rezistenţa) deducem o relaţie liniară între curentul electric şi tensiunea aplicată, precum se vede în graficul tensiune-curent de deasupra axei X.

domuri de lumină pe malul
râului Swan, din Perth,
Australia de vest
Gratitudine pentru imagine:
Gnangarra/Wikimedia
În ecuaţia 2, termenul (φ/e) este o constantă corespunzând energiei pierdute în interiorul juncţiunii de semiconductori p-n. (Pentru simplificare vom presupune că aceasta este egală pentru toate LED-urile.) Deoarce φ este necunoscută, nu am putea să determinăm constanta lui Plank din ecuaţia 2 doar prin măsurarea tensiunii de activare. Însă dacă tensiunea de activare (de prag) este măsurată pentru mai multe LED-uri de diferite lungimi de undă cunoscute, atunci puteam găsi o valoare pentru h prin trasarea graficului lui Va în funcţie de inversul lungimii de undă (1/λ).
Pentru că, rearanjând ecuaţia (2) ajungem la:
Va = hc/e(1/λ) + φ/c(3)
Astfel, graficul dependenţei lui Va de 1/λ va lua forma unei linii drepte având gradientul (panta) hc/e, din care constanta lui Planck poate fi uşor calculată, cunoscând valorile lui e şi c. Acest gradient poate fi determinat grafic, prin desenarea funcţiei şi prin trasarea liniei care aproximează cel mai bine punctele experimentale, sau prin calcularea matematică a regresiei liniarew2.
Regresia liniară ne conduce la următoarea valoare pentru gradient (m): m = 1.24811 x 10-6 Vm (volt-metri) Din aceasta, putem în sfârşit calcula constanta lui Planck. Deoarece m = hc/e, ajungem la:
h = em/c(4)
= 1.6022 x 10-19 x 1.24811 x 10-6/2.9979 x 108
= 6.6704 x 10-34 Js (joule secundă)
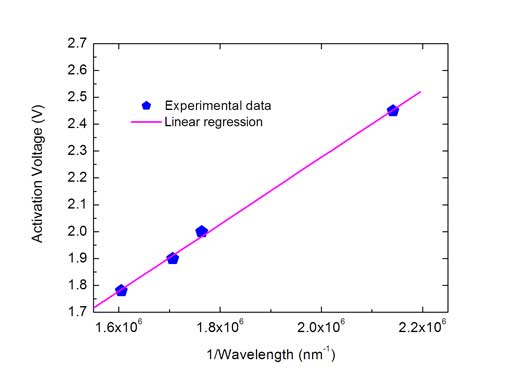
Pentru imagine mulţumim autorilor.
Valoarea obţinută prin acest experiment este destul de apropiată de valoarea acceptată a constantei lui Planck, de 6.62606957 x 10-34 Js – având o eroare de doar 0.7%w4. Valorile obţinute de elevi pot diferi un pic de aceasta, însă vor furniza o aproximare foarte acceptabilă a uneia dintre constantele fundamentale ale naturii.
Web References
- w1 – Pentru a afla mai multe despre lumină şi despre spectrul electromagnetic, vedeţi:
- Mignone C., Barnes R. (2011) Mai mult decât văd ochii: spectrul electromagnetic. Science in School 20:51-59.
- w2 – Calculatorul on-line al regresiei liniare care vă poate ajuta să analizaţi datele include:
- w3 – Pentru a afla cum vă puteţi construi propriul spectrometru, vedeţi:
- Tiele Westra M. (2007) A fresh look at light: build your own spectrometer. Science in School 4:30-34.
- w4 – Institutul Naţional pentru Standarde şi Tehnologie (NIST): valoarea de referinţă a constantei lui Planck.
Resources
- Proiectul ‘Sixty Symbols’ din cadrul Universităţii din Nottingham a produs un material video ce explică importanţa constantei lui Planck.
Review
Acest articol prezintă un experiment simplu şi practic ce poate fi folosit pentru a verifica valoarea constantei lui Plank, care este deseori folosită în fizica cuantică. Experimentul este uşor de reprodus în ora de clasă, materialele folosite fiind unele obişnuite în laboratoarele de fizică. Experimentul poate fi folosit fie ca o demonstraţie în ora de clasă, fie ca o cercetare individuală realizată de către elevi.
Teorita implicată în acest subiect poate părea iniţial prea abstractă pentru a fi înţeleasă de elevi, dar un astfel de experiment îi va ajuta să-şi clarifice anumite concepte şi să înţeleagă mai bine teoriile implicate. Articolul şi experimentul demonstrează câteva concepte foarte importante, precum:
- efectul foto-electric, unde ‘pachete discrete de energie’ sunt absorbite de un material şi determină o diodă să emită unde electromagnetice;
- tensiunea de deschidere a diodelor;
- calcularea constantei lui Planck.
Catherine Cutajar, Malta





