Fundamentos en el Aula: midiendo la constante de Planck Teach article
Traducido por José María Cordobés. Haciendo investigación en el aula y enseñando a los alumnos cómo calcular la constante de Planck con un experimento sencillo

Akimbomidget/Wikimedia
Cuando hablamos de medir constantes físicas fundamentales, como la velocidad de la luz o la de la fuerza de la gravedad, seguramente pensamos en famosos y sofisticados experimentos, -pero equipos existentes en los laboratorios corrientes de Física, se pueden utilizar para calcularlas.
La constante de Planck puede parecer algo extraño y difícil de entender, comparado con la velocidad de la luz, pero juega un papel de primera importancia en la comprensión del comportamiento de la materia a escala subatómica. Es la piedra angular de la mecánica cuántica que describe el comportamiento tan extraño de las partículas a ese nivel. En la teoría cuántica, tanto la energía como la materia están compuestas de partículas. Por ejemplo, la luz y cualquier otra radiación electromagnéticaw1, consisten de partículas llamadas fotones
Imagen de dominio
público/Wikimedia
La constante de Planck, llamada así en honor del físico alemán Max Karl Planck (1858-1947), permite entender la energía de los fotones en función de la longitud de onda de la radiación asociada, según la ecuación:
Ep = hc/λ
Dondo Ep es la energía de un fotón (en julios), h es la constante de Planck, c es la velocidad de la luz en el vacío, y λ es la longitud de onda de la radiación.
Sorprendentemente, aunque el valor de la constante de Planck es extraordinariamente pequeño, hemos ideado un método para calcular su valor con un experimento en el aula. La actividad no necesita ningún equipamiento especial -algunos diodos emisores de luz de colores diversos (LEDs) y aparatos eléctricos de uso común. Esta actividad la pueden realizar estudiantes desde 16 años hasta postgraduados.
¿Cómo funciona un LED?
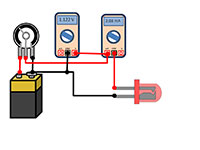
la respuesta de cada LED a
las magnitudes diferencia de
potencial y corriente
eléctrica. De izda a dcha:
batería, potenciómetro o
reostato, voltímetro,
amperímetro, LED
Imagen propuesta por los
autores
Los LEDs funcionan cuando dos semiconductores, uno de tipo n (con exceso de electrones) y otro de tipo p (con exceso de huecos), se ponen en contacto. Cuando una corriente eléctrica se hace pasar a través de esta unión, llamada unión p-n, la recombinación de electrones y huecos libera energía en forma de fotones.
El color de la luz emitida por un LED depende de la energía de los fotones, que se puede variar cambiando la composición química de los semiconductores. Los LEDs más comunes están compuestos de aleaciones de Galio, Arsénico y Aluminio, y variando la proporción de estos constituyentes, se consigue emisión de luz de colores dentro del espectro visible, como rojo y verde, o fuera de esas frecuencias, como ultravioleta o infrarrojo.
En la luz visible, la longitud de onda es lo que determina su color. El ojo humano es sensible a la luz en el rango de longitudes de onda de 390 a 700 nanometros (0,00039-0,0007 mm). Somos capaces de percibir el color violeta y el rojo como longitudes de onda más corta y más larga respectivamente. Sirve de ejemplo el LED emisor de luz verde con una longitud de onda de 567 nanometros.
Los LEDs que usamos en este experimento dan distinto color ya que son diferentes sus voltajes umbral para los que los electrones son producidos. Midiendo este voltaje y conociendo los valores de la longitud de onda de la luz emitida, podemos calcular el valor de la constante de Planck.
Materiales
- Cuatro LEDs que emiten luz roja, color naranja, verde y azul respectivamente. Los LEDs no tienen color por sí mismos, salvo cuando emiten luz debido al montaje experimental
- Batería de 9 Voltios
- Dos polímetros (uno para ser usado como voltímetro y otro como amperímetro)
- Un potenciómetro o reostato de 1 K?
Montaje
- Construya el circuito tal como indica el diagrama de arriba. Conecte el amperímetro en serie con el LED para medir la intensidad de corriente que pasa por él y el voltímetro en paralelo para medir la diferencia de potencial en el LED. El voltaje aplicado puede variarse con el potenciómetro o reostato.
- Vaya variando el voltaje a intervalos de 0,05 V desde 0 a 3 V y mida la intensidad de corriente en cada caso. Observe que cuando la corriente a través del LED es pequeña, éste no emite luz, aunque el amperímetro detecte paso de corriente. Para proteger el LED, tenga la precaución de mantener la intensidad de corriente por debajo de 5 mA.
- Para cada LED, haga una gráfica de Intensidad de corriente frente a Voltaje, de modo análogo a las mostradas arriba. En cada gráfica, trate de dibujar la línea recta que pase por la mayoría de los puntos obtenidos. Si los puntos se encuentran cerca de esa recta, quiere decir que hay una relación lineal entre el voltaje aplicado y la intensidad de corriente eléctrica en ese rango de medidas de la gráfica.
- 4. Por último, determine la diferencia de potencial de activación (Va) a partir de los datos obtenidos, es decir, el valor para el que la intensidad de corriente aumenta linealmente con el voltaje. Puede obtenerse a partir de la gráfica extrapolando la línea recta que representa la respuesta lineal hasta que intercepte el eje OX. Puede hacerse con una regla o de un modo matemático, mediante regresión lineal a partir de los puntos situados en la zona linealw2.
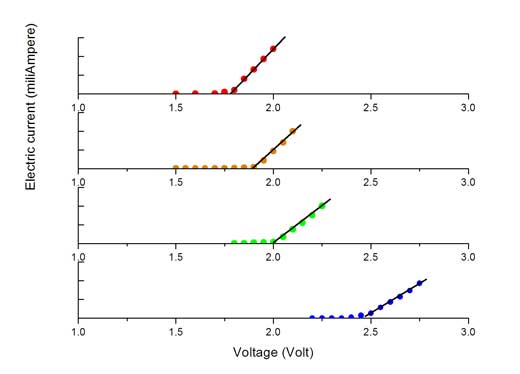
Imagen proporcionada por los autores
Para obtener un valor más exacto de Va, para cada color de los LEDs, se puede calcular un valor medio de los resultados obtenidos por varios estudiantes.
Valores típicos de voltajes de activación obtenidos en este experimento se muestran a la derecha, junto con los valores de la longitud de onda de la luz emitida por cada LED. Se pueden facilitar a los alumnos estos valores de las longitudes de onda para la siguiente fase de la actividad. De otro modo, las longitudes de onda pueden ser medidas con un espectrómetro tal como se describe en la página web mostrada debajo w3.
| Color LED | Longitud de onda típica, λ (cm) | Voltaje de activación, Va (V) |
|---|---|---|
| Rojo | 623 | 1.78 |
| Naranja | 586 | 1.90 |
| Verde | 567 | 2.00 |
| Azul | 567 | 2.45 |
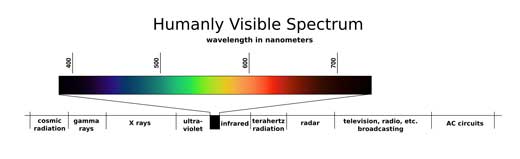
Imagen tomada de entirelysubjective/Flickr
Análisis de resultados
Como vimos anteriormente, la energía de los fotones emitidos, Ep (medida en joules), está relacionada con la constante de Planck (h), la velocidad de la luz en el vacío (c), y la longitud de onda de la luz λ:
Ep = hc/λ (1)
En este experimento conocemos las longitudes de onda de la luz emitida por los LEDs, y conocemos el valor de c (2,9979 x 108 ms-1). ¿Cómo podemos calcular el valor de la constante de Planck a partir de los valores de Va medidos? Consideremos cómo funcionan los LEDs.
Cuando un LED se conecta a voltajes pequeños, la energía no es suficiente para producir fotones y la corriente eléctrica originada es muy pequeña. A partir de cierto voltaje, el LED empieza a emitir fotones: este es el voltaje de activación, Va. El voltaje mínimo para LEDs de distintos colores está relacionado con la energía de los fotones emitidos Ep (ecuación 2). De hecho, igual que Ep, Va está relacionada matemáticamente con la constante de Planck y la longitud de onda de la luz emitida, como se muestra en la ecuación de abajo:
Va = Ep/e + λ/c (2)
Dondo e es la carga del electrón (1,6022 x 10?19 culombios). Para voltajes superiores a Va, la intensidad de corriente está determinada por la resistencia eléctrica de los LEDs. Aplicando la ley de Ohm, Voltaje (V) =Intensidad de corriente (I) x Resistencia (R), se deduce una relación lineal entre la intensidad de corriente y el voltaje aplicado, como se observa en las gráficas (V, I) más arriba

colores en la orilla de Swan
River, Perth, Australia
Imagen cortesía de
Gnangarra/Wikimedia
En la ecuación (2), el término (?/e) es una constante que da la pérdida de energía en la unión p-n del semiconductor. (Para mayor sencillez, podemos suponer que esta constante es igual para todos los LEDs). Puesto que ? es desconocida, no es posible a partir de la ecuación 2 determinar la constante de Planck midiendo sólo el voltaje de activación. Sin embargo, si éste es medido para varios LEDs que emiten en diferentes longitudes de onda, podemos calcular h a partir de la gráfica Va frente a la inversa de la longitud de onda (1/?).
De este modo, reescribiendo la ecuación (2) tenemos esta ecuación:
Va = hc/e(1/λ) + φ/c (3)
Por tanto, la gráfica Va frente a 1/λ nos da una línea recta con pendiente hc/e, a partir de la cual se puede calcular fácilmente la constante de Planck, suponiendo conocidos los valores de e y c. Esta pendiente puede ser obtenida a partir de la gráfica dibujando una línea recta que pase por la mayor parte de los puntos, o de forma matemática, calculando la regresión linealw2.
Usando la regresión lineal se obtiene el siguiente valor para la pendiente (m): m = 1,24811 x 10-6 Vm (voltios metro) A partir de ella, tenemos la constante de Planck. Es decir, tenemos m = hc/e, luego,
h = em/c (4)
= 1,6022 x 10-19 x 1,24811 x 10-6/2,9979 x 108
= 6,6704 x 10-34 Js (julios.segundo)
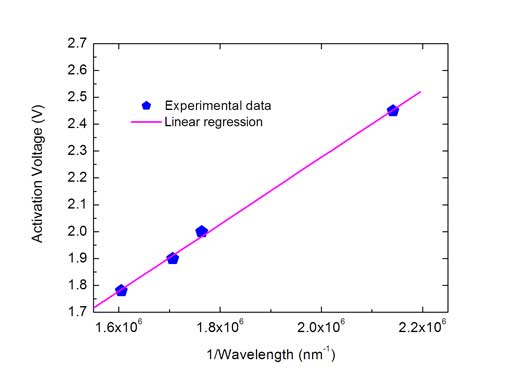
Imagen de los autores
Este valor se aproxima bastante bien con el valor aceptado para la constante de Planck de 6,626068957 x 10-34 J.s –un error del 0,7%w4. El valor obtenido por los estudiantes puede ser un poco distinto, pero aún así supone una buena aproximación a la que es una de las constantes fundamentales de la naturaleza.
Web References
- w1 – Para aprender más sobre la luz y el espectro electromagnético, consultar:
- Mignone C., Barnes R. (2011) Más allá de lo que el ojo ve: el espectro electromagnético. Science in School 20:51-59.
- w2 – Cálculo de regresión lineal online que puede ayudar al análisis de sus datos incluye:
- w3 – Para ver cómo construir un espectrómetro, consultar:
- Tiele Westra M. (2007) Una mirada nueva a la luz: construye tu propio espectrómetro. Science in School 4:30-34.
- w4 – the National Institute of Stanfdards and Technology (NIST): referencia del valor de la constante de Planck.
Resources
- El Proyecto “Sixty Symbols” de la Universidad de Nottingham ha elaborado un vídeo corto explicando la importancia de la constante de Planck
Review
Este artículo describe un experimento sencillo y práctico para calcular el valor de la constante de Planck, que es fundamental en la Física Cuántica. La práctica se puede llevar a cabo en el aula, ya que los materiales necesarios se encuentran en un laboratorio de Física. Se puede realizar bien como una demostración en la clase, o como una actividad de investigación a desarrollar por los alumnos.
La Teoría implicada en esta actividad puede parecer demasiado abstracta a los alumnos y de difícil comprensión, pero sin duda les ayudará a entender algunos conceptos y a iniciarles en esta parte tan importante de la Física. Este artículo y los experimentos ayudan a comprender conceptos importantes, como:
- El efecto fotoeléctrico, en el que cantidades discretas de energía son absorbidas por un material y hace que un diodo a emita ondas electromagnética
- Voltaje de activación en diodos
- cálculo de la constante de Planck
Catherine Cutajar, Malta
