Supporting materials
À descoberta da escala do espaço: dedução da fórmula da distância estelar (Word)
À descoberta da escala do espaço: dedução da fórmula da distância estelar (Pdf)
Download
Download this article as a PDF

Traduzido por Pedro Augusto. Como medem os astrónomos as distâncias das estrelas? O uso de uma máquina fotográfica digital para registar movimentos de paralaxe é um método preciso e autêntico que pode ser usado em sala de aula.
Os astrónomos são observadores remotos, separados por grandes distâncias dos seus objetos de estudo. Saber a distância dos objetos celestes é crucial: esta é um fator-chave na distinção entre um objeto muito brilhante e distante e um muito mais próximo mas com brilho próprio inferior – assim, podemos mais facilmente descobrir de que objeto se trata. Estrelas isoladas e galáxias inteiras podem parecer semelhantes – até sabermos que umas estão biliões de vezes mais longe do que as outras e, assim, em realidade são triliões de vezes mais brilhantes.
O método astronómico mais importante na medição de distâncias entre a Terra e as estrelas é a paralaxe – o deslocamento aparente em posição de um objeto visto consoante o observador muda o seu local. Damos conta do efeito de paralaxe quando olhamos para fora de uma janela de um comboio em movimento: os objetos mais próximos parecem deslocar-se bem mais depressa do que os mais longínquos. Usando este efeito podemos determinar a distância a um objeto medindo a alteração aparente da sua posição quando o nosso local como observadores muda.
O desafio, claro, é a precisão. Como podemos fazer medições de distâncias baseadas em paralaxe tão precisas quanto for possível? Neste segundo artigo sobre a medição de distâncias com recurso à paralaxe usamos um método autêntico, muito semelhante ao utilizado pelos astrónomos, que foi adaptado para sala de aula (ver o anterior artigo em Pössel, 2017). Em vez de utilizar aparelhos que medem ângulos (como no artigo anterior, que foi baseado em medições com um teodolito) para determinar a distância a uma ‘estrela’ vamos tirar fotografias de diferentes posições e utilizar estas para as medições que precisamos para calcular a distância à nossa estrela.

Uma variação deste método fotográfico, descrito mais à frente neste artigo, é ainda mais autêntica e precisa, embora um pouco mais complicada. Envolve a utilização de um ponto fixo de referência fora da sala de aula – tal como os astrónomos usam objetos de fundo muito distantes (e.g. galáxias ativas chamadas quasares) como pontos de referência fixos quando medem paralaxes estelares, em vez de confiarem que os seus telescópios apontam exatamente na mesma direção em cada observação.
Para estas atividades vai ser necessária uma máquina digital montada (se possível) numa bancada ótica (ver figura 1). As atividades podem ser feitas em grupo. Contar com cerca de 30 minutos para a montagem e as medições e outros 30 minutos para a análise e os cálculos.

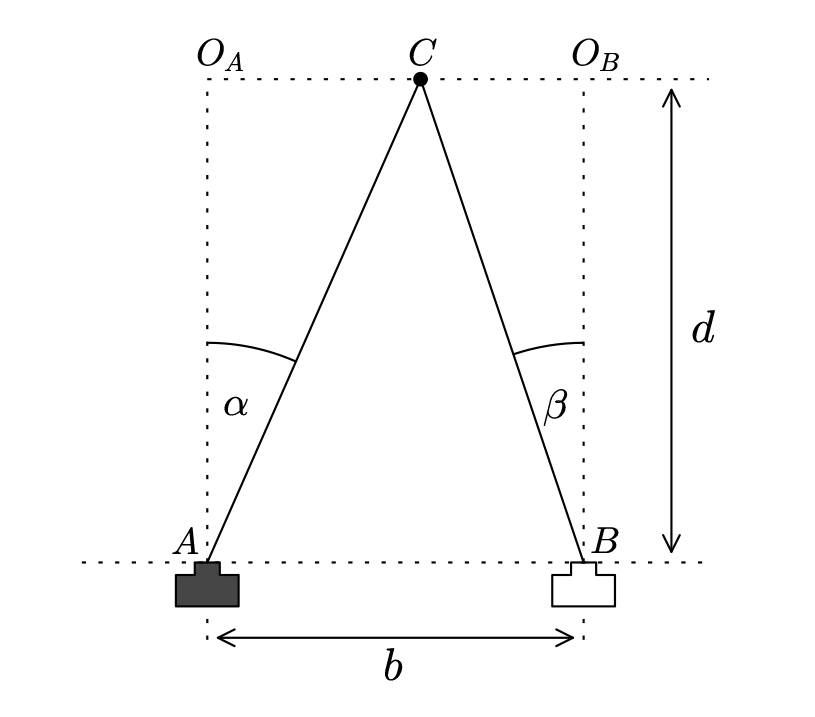
A situação experimental está representada na figura 2. Aqui, b representa o deslocamento ao longo da linha-de-base da máquina fotográfica (sobre a bancada ótica ou sobre a mesa) entre a primeira e a segunda posições (A e B), enquanto C é a posição da estrela-modelo e d a distância da linha-de-base da máquina fotográfica à estrela – ou seja, a distância que pretendemos calcular.
Os passos para o cálculo da distância d são os seguintes:
Ao contrário dos teodolitos, as máquinas fotográficas não permitem a medição direta de ângulos. Assim, precisamos de relacionar a localização das imagens da estrela no ecrã do detetor de imagens da máquina fotográfica com o ângulo dos raios de luz da estrela quando a máquina fotográfica está em diferentes posições.
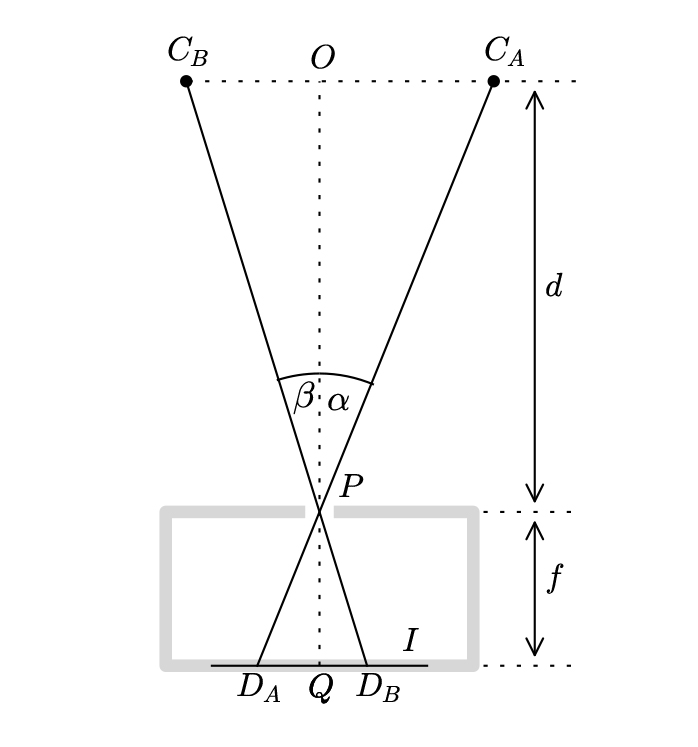
O ponto de vista da máquina fotográfica é mostrado na figura 3. O local aparente da estrela é CA quando a máquina fotográfica está na primeira posição (A) e a sua imagem vai estar localizada em DA no ecrã. De forma semelhante, depois de deslocar a máquina fotográfica para B, a localização aparente da estrela é em CB e a respetiva imagem em DB. (Aqui o segmento de reta OQ representa a distância entre o plano de imagem da máquina fotográfica e o plano paralelo que contém a estrela.) O comprimento CBCA é a distância b na figura 2, enquanto os ângulos a e ß se mantêm os mesmos.
A formula é:
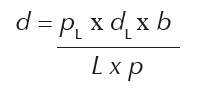
Onde:
d = distância à estrela
L = comprimento do objeto de calibração
b = distância em que a máquina fotográfica foi deslocada (de CA para CB)
dL = distância do objeto de calibração à linha-de-base da máquina fotográfica (ao longo da reta OQ)
p = distância como o número de pixeis entre imagens da estrela (em DA e DB)
pL= comprimento em número de pixeis da imagem do objeto de calibração
Quanto tiver determinado o valor de d, usou com sucesso a medição da paralaxe para determinar a distância à estrela.
Use agora a fita métrica para encontrar diretamente a distância d e compare-a com o valor calculado por paralaxe. Quão precisa foi a medição calculada?
Pode repetir esta atividade com a ‘estrela’ colocada a diferentes distâncias de forma a descobrir se a precisão das medições de paralaxe se altera com a distância (ver a secção abaixo ‘Que precisão devemos esperar?’)
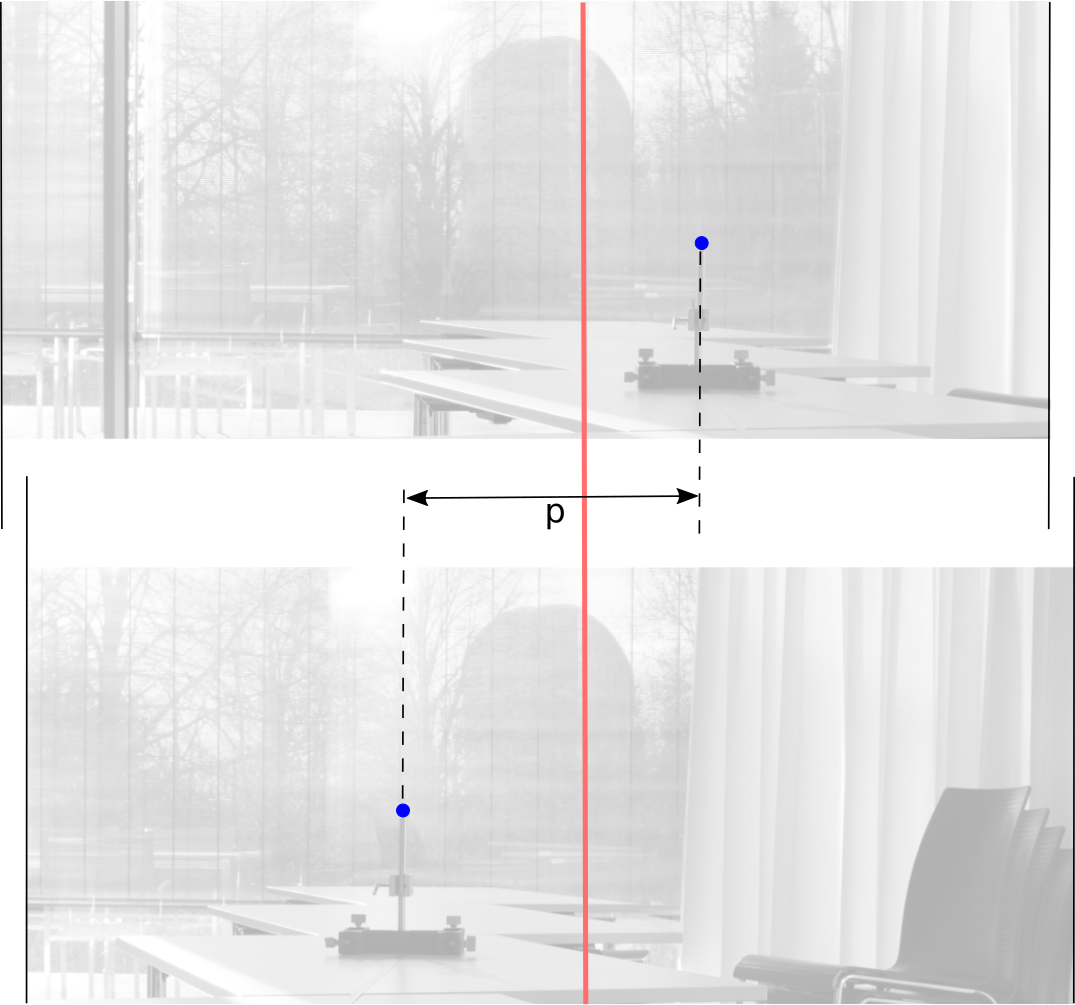
Para um ainda maior realismo astronómico, podemos adaptar o método da paralaxe fotográfica de forma a utilizar um objeto fora da sala de aula, que deve estar consideravelmente mais longe do que a ‘estrela’. Com este procedimento, em vez de depender da máquina fotográfica apontar na mesma direção conforme se move de A a B, escolhemos um objeto de referência distante que seja visível em cada uma das duas imagens. Depois medimos a distância em pixéis da imagem da estrela ao objeto de referência em cada imagem. Esta abordagem alternativa, que descrevemos aqui, deve proporcionar resultados mais precisos.
Bom, quão precisos são os resultados obtidos com este método melhorado? Os nossos dados sugerem que podem ser notavelmente precisos (comparados com o método das distâncias diretamente medidas), como mostrado na figura 5. O erro máximo relativo é de apenas 3.2%.
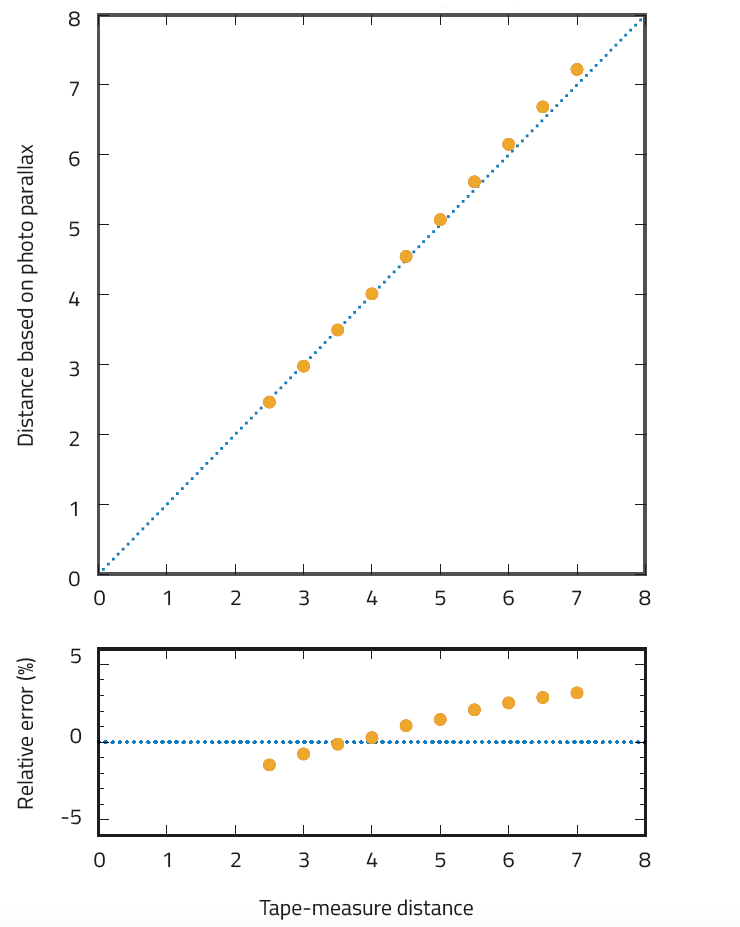
Note que a distâncias maiores há um aumento no erro relativo e no erro, de facto. Isto é devido a uma alteração da geometria: a distância à estrela-modelo torna-se grande comparada com a distância ao objeto de referência, de tal forma que o erro introduzido pela paralaxe do objeto de referência se torna cada vez maior.
Com o método de medição de ângulos simples descrito no artigo anterior (Pössel, 2017), a precisão da medição de distâncias era bastante mais baixa – usualmente dentro de cerca de 10%, como se mostra na figura 6. Assim, o método descrito neste artigo permite uma melhoria significativa na precisão em relação ao método anterior, onde as fontes dominantes de erro são as medições de ângulos.
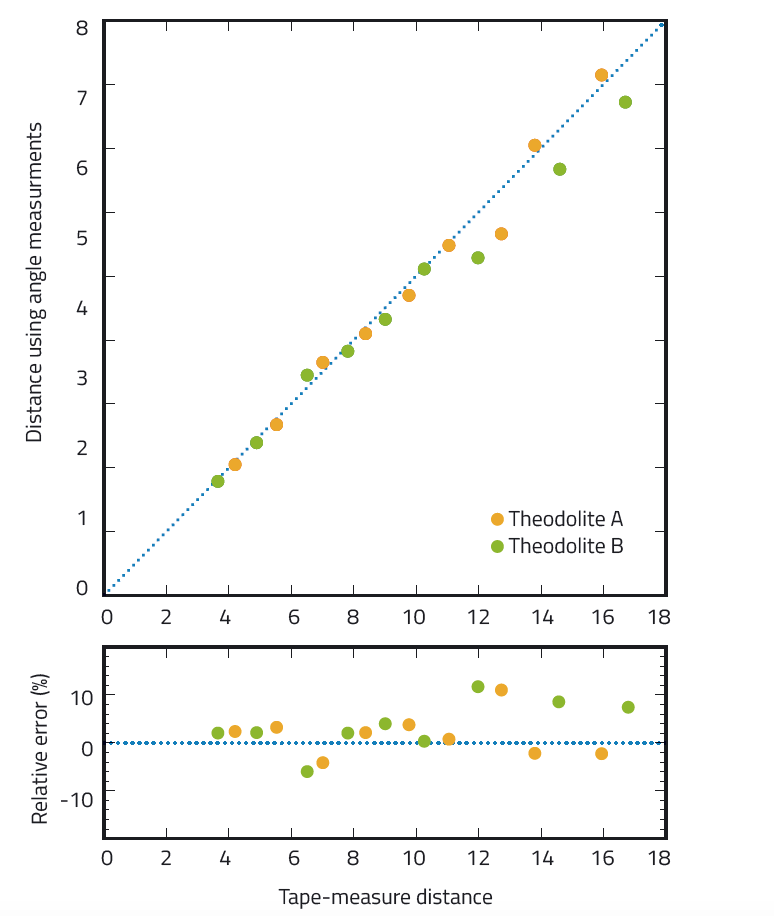
Pössel M (2017) Parallax: reaching the stars with geometry. Science in School 39: 40-44.
w1 – Uma dedução algébrica da fórmula para o cálculo da distância à estrela com recurso a triângulos semelhantes pode ser descarregada da secção de materiais adicionais.
Para informação em como efetuar medições de paralaxe astronómica reais com pequenos instrumentos, ver:
Cenadelli D et al. (2016) Geometry can take you to the Moon. Science in School 35: 41-46.
Cenadelli D et al. (2009) An international parallax campaign to measure distance to the Moon and Mars. European Journal of Physics 30: 35-46. doi: 10.1088/0143-0807/30/1/004
Hirshfeld AW (2013) Parallax: The Race to Measure the Cosmos. Mineola, NY, USA: Dover Publications. ISBN: 9780486490939
Variações destas experiências têm sido utilizadas em cursos de Astronomia laboratoriais há muito. Por exemplo:
De Jong ML (1972) A stellar parallax exercise for the introductory astronomy course. American Journal of Physics 40(5): 762-763. doi: 10.1119/1.1986635
Deutschman WA (1977) Parallax without pain. American Journal of Physics 45(5): 490. doi: 10.1119/1.11009
Este artigo descreve uma forma inovadora de encontrar distâncias a objetos celestes recorrendo ao método da paralaxe. É perfeitamente adequado a professores e alunos que tenham grande interesse em Fotografia e em Astronomia. Fornece o detalhe suficiente para ser possível calcular a distância a uma ‘estrela’ com um bom grau de confiança.
Esta atividade é ideal para ser realizada por um grupo de alunos avançados numa workshop em Astronomia e Fotografia.
Stephanie Maggi-Pulis, Secretariat for Catholic Education, Malta