Regras de simetria Understand article

Traduzido por Ana Luísa Carvalho. Todos sabem o que é simetria. No entanto, neste artigo, Mario Livio, do Instituto Científico do Telescópio Espacial Hubble, em Baltimore, nos EUA, explica como não só as formas, mas também as leis da natureza, podem ser simétricas.

Todos reconhecerão a mancha da figura em baixo à esquerda como simétrica, mas poucos sabem que a figura em baixo à direita também é considerada simétrica, em termos matemáticos precisos. Então, o que é verdadeiramente a simetria? E porquê este conceito é tão essencial, ao ponto de muitos cientistas o considerarem a base das leis da natureza?

Quando as coisas que deveriam ter-se alterado, não o fazem

A simetria representa imunidade a possíveis alterações – aquelas formas, frases, leis ou expressões matemáticas que permanecem inalteradas, após transformações específicas. Consideremos, por exemplo, a frase “Madam, I’m Adam”, que é simétrica quando lida de trás para a frente, letra por letra. Ou seja, a frase é a mesma, quando lida ao contrário. O título do documentário A Man, a Plan, a Canal, Panama, possui a mesma característica. As frases com este tipo de simetria são conhecidas como palindromas. Os palindromas têm um papel muito importante na estrutura do cromossoma Y, que determina o sexo masculino. Até 2003, os biólogos do genoma acreditavam que, devido ao facto de o cromossoma Y não possuir um parceiro (com o qual poderia trocar genes), a sua carga genética seria muito susceptível a mutações prejudiciais. No entanto, para sua surpresa, os investigadores que sequenciaram o cromossoma Y descobriram que este luta contra a sua própria destruição recorrendo a palindromas. Dos 50 milhões de letras do ADN cromossómico, cerca de 6 milhões formam sequências palindrómicas. Estas cópias “espelho” constituem cópias de segurança contra mutações prejudiciais, e permitem que o cromossoma, de certa forma, estabeleça sexo consigo próprio – as cadeias podem trocar posições.

Para figuras e formas bidimensionais, como os que desenhamos numa folha de papel, existem quatro tipos ‘rígidos’ de simetria (esticamentos e distorções não são permitidos) conhecidos como: reflexão, rotação, translação e reflexão de escorregamento.

Se olharmos bem à nossa volta, encontraremos facilmente simetria por reflexão – trata-se da simetria bilateral que caracteriza os animais. Desenha uma linha pelo meio de uma figura de uma borboleta (ver acima). Agora, dobra a figura, mantendo a linha central fixa. A sobreposição perfeita resultante indica que a borboleta permanece inalterada após aplicada a operação de simetria de reflexão ao longo da sua linha central.

Esta propriedade é também característica de muitas letras do alfabeto. Se puseres uma folha de papel com a frase ‘MAX IT WITH MATH’ (escrita verticalmente) em frente a um espelho, verás que a frase é a mesma.

A simetria rotacional também é facilmente encontrada na natureza. Se rodarmos um floco de neve 60, 120, 180, 240, 300 ou 360 graus em torno do seu eixo central (perpendicular ao seu plano), obteremos configurações indistintas umas das outras. Um círculo rodado de qualquer ângulo em trono de um eixo central perpendicular, permanece inalterado.

A simetria de translação é um tipo de resistência a alterações que pode ser encontrado em motivos que se repetem, como os da segunda figura. A translação implica deslocamento, de uma certa distância, ao longo de uma linha específica. Este tipo de simetria pode ser observado em muitos padrões clássicos de papel de parede, filas de janelas em prédios altos e até em centopeias.

Por último, são simétricas por escorregamento as pegadas resultantes de um caminhar esquerda-direita-esquerda-direita (ver abaixo). Neste caso, a transformação consiste numa translação (ou escorregamento), seguida de uma reflexão numa linha paralela à direcção de deslocamento (a linha a tracejado).

Todas as simetrias que descrevemos até agora são simetrias de forma – aquelas que conseguimos visualizar com os nossos próprios olhos. As simetrias por detrás das leis da natureza estão, de certa forma, relacionadas com as que descrevemos, mas, em vez de se referirem à forma, dizem respeito a uma questão distinta: que transformações podem ocorrer à nossa volta que deixem inalteradas as leis que descrevem todos os fenómenos observáveis?

Regras de simetria

Colectivamente, as ‘leis da natureza’ descrevem o conjunto de regras que supostamente explicam tudo o que observamos no universo. Antes do século XVII, era inconcebível a existência de um tal conjunto de regras e apenas com os trabalhos de gigantes como Galileu Galilei (1564-1642), René Descartes (1596-1650) e, particularmente, Isaac Newton (1642-1727) esta noção se tornou clara. Subitamente, fenómenos tão diversos como a queda de maças, marés e o movimento dos planetas foram considerados como resultantes de uma lei: a lei da gravidade de Newton.

Da mesma forma, baseado-se nos resultados experimentais de Michael Faraday (1791-1867), o físico escocês James Clerk Maxwell (1831-1879) conseguiu explicar todos os fenómenos eléctricos, magnéticos e luminosos, com apenas quatro equações! Pensa nisto por uns instantes – todo o mundo do electromagnetismo em quatro equações.

Sabe-se que as leis da natureza obedecem a algumas das operações de simetria que já descrevemos, mas também a outras, de carácter mais esotérico. Para começar, as leis são simétricas por translação. A manifestação desta propriedade é simples: usando as mesmas leis, poderás descrever os resultados de qualquer experiência, quer a tenhas realizado em Nova Iorque, Los Angeles, no outro lado da Via Láctea ou numa galáxia a um bilião de anos-luz daqui. Como é que sabemos que isto é verdade? Porque observando as galáxias em todo o universo, verificamos não só que a lei da gravidade é a mesma em todo o lado, mas também que os átomos de hidrogénio nos limites do universo observável obedecem precisamente às mesmas leis do electromagnetismo e da mecânica quântica que vigoram aqui no planeta Terra.

As leis da natureza também são simétricas por rotação – as leis são precisamente as mesmas quer consideremos direcções medidas a partir do norte ou da cafetaria mais próxima – a física não tem qualquer preferência por direcções no espaço.

Se as leis não possuíssem esta característica notável de simetria translacional e rotacional, nunca compreenderíamos as diferentes partes do cosmos. Além disso, mesmo aqui na Terra, se as leis não fossem simétricas, as experiências teriam que ser repetidas em cada laboratório do globo.

É necessária prudência e saber distinguir entre simetria de forma e simetria das leis. Os gregos da antiguidade pensavam que as órbitas dos planetas em torno do Sol eram simétricas por rotação, ou seja, circulares. De facto, a simetria rotacional aplica-se não à forma da órbita, mas sim à lei da gravidade de Newton. Isto significa que as órbitas podem ser (e, na realidade, são) elípticas, mas poderão adoptar qualquer orientação no espaço (ver acima).

No meu parágrafo inicial, mais do que dizer que as leis obedecem a determinadas simetrias, afirmei categoricamente que a simetria pode estar na origem das leis. Qual o significado desta afirmação?

A origem das leis naturais

Imagina que nunca terias ouvido falar de flocos de neve e alguém te pedia que adivinhasses a sua forma. Obviamente, seria uma tarefa impossível. Tanto quanto saberias, o floco de neve poderia parecer-se com uma chávena, a letra S ou o Bugs Bunny.

Mesmo que alguém te dê um dos raios de um floco de neve (a, em cima) e te diga que essa é uma parte da forma completa, isso não te servirá de muito. O floco de neve poderia ter, por exemplo, a configuração b, da figura acima. No entanto, se te disserem que um floco de neve é simétrico por rotações de 60 graus em torno do seu centro, poderás usar esta informação de uma forma eficaz. A simetria limita imediatamente as configurações possíveis e apenas poderás obter flocos de neve com 6, 12, 18 raios, … Assumindo que a natureza optaria pela solução mais simples e económica, uma possibilidade razoável seria um floco de neve com seis raios (c, em cima). Por outras palavras, a exigência de uma simetria de forma guiou-nos na direcção correcta.

Da mesma forma, a imposição de que as leis da natureza sejam simétricas sob certas transformações não só dita a forma dessas leis, mas também, em alguns casos, necessita da existência de forças ou de partículas elementares ainda desconhecidas. Deixem-me explicar-vos isto, usando dois exemplos interessantes.

Um dos principais objectivos de Einstein ao descrever a relatividade geral era elaborar uma teoria que mostrasse que as leis da natureza são exactamente as mesmas para todos os observadores. Ou seja, as leis teriam que ser simétricas sob qualquer alteração do nosso ponto de vista, no espaço e no tempo (em física, isto é conhecido como ‘covariância geral’). Um observador sentado na carapaça de uma tartaruga gigante deduziria as mesmas leis que um observador num carrocel ou num foguetão em aceleração. Se as leis são universais, como podem elas depender do facto do observador se encontrar em aceleração?

Embora a exigência de Einstein por simetria fosse certamente razoável, ela não era, de forma alguma, trivial. Afinal, o número anual de ferimentos causados por aceleração ou desaceleração rápida (como nos acidentes de automóvel) nos Estados Unidos, provam que nós sentimos a aceleração. Sempre que um avião entra num poço de ar, nós sentimos o estômago subir até à garganta – parece existir uma distinção óbvia entre movimento uniforme e movimento acelerado. Nesse caso, como podem as leis da natureza ser as mesmas para observadores em aceleração, se esses observadores, aparentemente, estão sujeitos a forças adicionais?

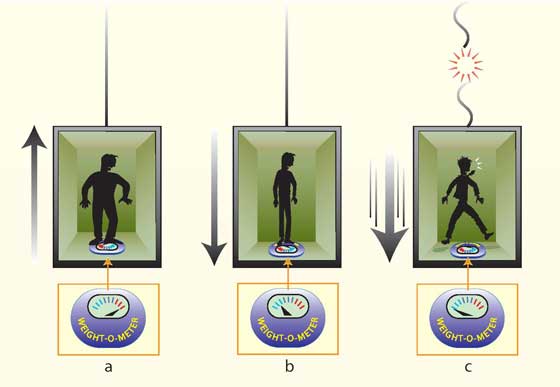
Considera a seguinte situação. Se te puseres em cima de uma balança dentro de um elevador em subida, os teus pés exercerão uma pressão maior sobre a balança – esta registará um peso superior (a, em cima). No entanto, o mesmo aconteceria se, de alguma forma, a gravidade se tornasse mais forte num elevador parado. Num elevador em aceleração, mas no sentido descendente, sentirás gravidade mais fraca (b, em cima). Se o cabo do elevador se partisse, tu e a balança cairiam livremente e a balança registaria um peso de zero (c, em cima). Sendo assim, a queda-livre equivale a alguém, miraculosamente, ter desligado a gravidade e esta ser zero. Isto levou Einstein, em 1907, a uma conclusão fundamental: a força da gravidade e a força resultante da aceleração são de facto a mesma. Esta unificação foi designada ‘princípio de equivalência’, e significa que a aceleração e a gravidade são duas facetas de uma mesma força – são equivalentes.

Numa conferência em Kyoto em 1922, Einstein descreveu este momento de inspiração de 1907: “Encontrava-me sentado no gabinete de patentes em Berna, quando de repente me ocorreu um pensamento: se uma pessoa cair livremente, não sentirá o seu próprio peso. Fiquei surpreso. Este simples pensamento causou-me uma profunda impressão. Levou-me a elaborar a teoria da gravitação.”

O princípio da equivalência é a demonstração da existência de uma simetria invasiva; as leis da natureza – tal como expressas pelas equações da relatividade geral de Einstein –  são as mesmas em todos os sistemas, incluindo aqueles que se encontram em aceleração. Nesse caso, então porquê existem diferenças aparentes entre o que é observado num carrocel e o que é observado num laboratório em repouso? A relatividade geral providencia-nos uma resposta surpreendente. As diferenças existem apenas no ambiente, não nas leis. Do mesmo modo, as direcções para cima e para baixo só parecem diferentes aqui na Terra, devido à gravidade do planeta. As leis da natureza, por si sós, não possuem direcções preferenciais (são simétricas por rotação); não distinguem entre para cima e para baixo. De acordo com a relatividade geral, os observadores num carrocel sentem a força centrífuga, que é equivalente à gravidade. A conclusão é verdadeiramente excitante: a simetria das leis sujeitas a qualquer alteração nas coordenadas espaço-tempo, necessita da existência da gravidade! Isto explica porque é que a simetria é a fonte das forças. A necessidade de simetria não dá outra alternativa à natureza: a gravidade tem que existir.

Download

Download this article as a PDF