Malditas mentiras Understand article
Traduzido por Ana Luísa Carvalho. Possui mais do que o número médio de orelhas? O seu salário é inferior à média? Quando chegará o próximo autocarro? Ben Parker tenta convencer-nos do valor das estatísticas – quando usadas correctamente.

de orelhas?
Imagem cortesia de Lisa Kyle
Young/iStockphoto
Tenha sido Mark Twain, ou Benjamin Disraeli, o primeiro a introduzir a ideia de que existem três tipos de falsidade – “Mentiras, malditas mentiras, e estatísticas” – a verdade é que o sentimento persiste. Os especialistas em estatística são manipuladores, enganadores, dispostos a poluir as nossas mentes com informação insignificante e tendenciosa, que nos fará votar no seu partido político favorito, escolher o seu creme comprovadamente eficaz, ou comprar a comida que os seus gatos preferem. Para mim, como especialista em estatística, está na hora de derrubar alguns mitos.
Exactamente 96,4% do nosso mundo moderno gira em torno das estatísticas e, embora existam por aí algumas estatísticas surpreendentemente más, eu espero convencer-vos que o problema reside geralmente na forma como nos são apresentadas.
Orelhas, para que vos quero
Eu podia apostar que você, caro leitor, possui mais do que o número médio de orelhas. Porquê? Assumamos que existem 6 biliões de pessoas neste nosso mundo super-povoado, e que mais de 99% dessas pessoas possuem duas orelhas. Existe um número excepcional de pessoas que, devido a acidente ou problema congénito, possuem apenas uma ou mesmo nenhuma orelha. Desconheço a existência de pessoas com três orelhas (infelizmente o Comandante Kirk é uma personagem fictícia, mas ele possuía realmente três orelhas: uma orelha esquerda, uma orelha direita e uma última fronteira). Quando calculamos a média (somamos o número total de orelhas que a humanidade possui, e dividimos pelo número de pessoas), obtemos o resultado
o que é pouco menos de dois. Isto significa que, uma vez que a maior parte das pessoas possui duas orelhas, elas possuem ligeiramente mais do que o número médio, pelo que, quase sempre, eu ganharia a aposta.
O que é que isto significa?
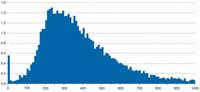
semanal 2004/2005: Número
de indivíduos (milhões),
Grã-Bretanha. Fonte:
Households Below Average
Income (HBAI)
1994/95-2004/05. Clique na
imagem para alargar.
Departamento para o Trabalho
e Pensões
Claro que isto não passa de pedantismo de um profissional de estatística. No entanto, não faltam por aí exemplos menos tolos. Estatísticas de como um grupo de pessoas ganha menos que uma certa percentagem do salário médio nacional, são frequentemente usadas como estratégia política. É comum ler, em jornais, comentários sobre o quanto é chocante que as pessoas ganhem apenas uma percentagem do rendimento nacional, e que é tudo culpa do governo Trabalhista, da administração Conservadora anterior, da União Europeia ou das manchas solares.
De acordo com o Departamento para o Trabalho e Pensões do Reino Unido (ver figura acima), a distribuição de rendimentos é tal, que são relativamente poucas as pessoas que ganham grandes somas de dinheiro (infelizmente, os profissionais de estatística não estão incluídos neste grupo). Isto significa que o rendimento médio, calculado pelo Departamento em 427 libras por semana, para um casal sem filhos (Departamento para o Trabalho e Pensões, 2006), é muito superior ao que a maioria das pessoas recebe, uma situação semelhante ao cálculo médio de orelhas, exemplificado acima. Um grupo pequeno de pessoas extraordinárias, por possuírem menos do que duas orelhas ou por receberem grandes quantias de dinheiro, distorcem a média da situação da maioria das pessoas.
Claro que as pessoas depressa perceberam que esta forma de cálculo, somar tudo e dividir pelo número de coisas que somámos, mais vulgarmente referida como média, podia ser mal interpretada. Assim, na prática adoptou-se o conceito de mediana. Se puséssemos todas as pessoas do Reino Unido numa fila de acordo com o seu rendimento, a mediana do salário seria o da pessoa que ficasse a meio da fila. Na prática, a mediana, cerca de 349 libras por semana neste exemplo, dá-nos uma ideia mais correcta do que é o valor típico.
Pelo menos chegámos a algo que faz sentido – mas será que todos entendem este problema básico que é transmitir ideias usando médias? Apesar de tudo, a obrigação de um bom jornalista é ou não é reunir ideias e apresentar a verdade de uma forma que o público consiga entender?
Infelizmente, factos precisos e informação correctamente interpretada nem sempre vendem jornais ou transmitem a verdadeira mensagem política.
Alisando as rugas

cliente ficou satisfeita
Imagem cortesia de Al
Wekelo/iStockphoto
iores que os jornalistas, mas não tanto como os políticos, são os publicitários. Num anúncio televisivo recente, uma empresa de cosmética afirma que o seu mais recente creme anti-rugas satisfez 8 em cada 10 clientes, baseando-se na inquirição de 134 pessoas. Podemos talvez perdoar o pequeno tamanho da amostra – e até mesmo o arredondamento (134 x 8/10 = 107.2), o que significa que tiveram 0.2 de um cliente a também experimentar o creme – mas a questão crucial é: como foi o inquérito realizado?
Parece-me dúbio perguntar a 134 clientes se gostaram do produto – se as pessoas são já clientes, e compraram o produto voluntariamente, talvez não seja o mais justo dos exemplos. Porque é que alguém compraria um produto de que não gosta? Num teste com características realmente científicas, proceder-se-ía à comparação do desempenho do produto com um outro creme de outra marca, ou mesmo um placebo, e, escolhendo pessoas ao acaso, verificar-se-ía se tinham sentido um efeito positivo com esse produto.
Não há nada de errado com a publicidade, por si só; alguns filósofos afirmam que a publicidade é vital numa democracia forte. Os publicitários têm todo o direito de informar as pessoas sobre o seu produto e promover os seus benefícios. No entanto, o que não é aceitável é mascarar o marketing com ciência; sem explicar o método, a estatística ‘8 em cada 10’ não possui qualquer significado. É tão incorrecto como dizer “O nosso veículo possui uma velocidade máxima de 500 milhas por hora”, omitindo que esta velocidade só se verifica se o veículo cair de um avião em pleno voo: é verdade, mas é também enganador. Usar este tipo de sondagem em publicidade é o mesmo que mentir.
Vêm três de cada vez
Talvez seja injusto culpar as empresas de transporte, em vez dos próprios dados estatísticos. Existem factos estatísticos reais, difíceis de interpretar e muito pouco intuitivos. Imagina que estás numa paragem à espera de um autocarro, olhas para o horário, se não se encontrar vandalizado, e neste consta que circulam cinco autocarros por hora. Quanto tempo calculas que terás que esperar pelo próximo autocarro?
A lógica comum diz-te que, se circulam 5 autocarros por hora, então o tempo médio entre autocarros é 12 minutos. Assumindo que chegaste à paragem a qualquer momento deste período, calcularias esperar 6 minutos pelo autocarro. Boa lógica, mas, infelizmente, quase sempre errada.
Nós sabemos que os autocarros não circulam ao minuto. Eles podem sair do terminal a tempo, mas factores não controláveis irão alterar o seu progresso de diferentes formas, pelo que temos que assumir que o padrão de chegadas à nossa paragem varia significativamente. A distribuição exacta que escolhermos pode variar – podemos, por exemplo, assumir que o tempo entre chegadas segue uma distribuição exponencial – mas o importante é que os autocarros nunca chegarão a tempos regulares. Então, voltemos a imaginar que chegamos à nossa paragem a qualquer momento – quanto tempo teremos então que esperar pelo próximo autocarro?
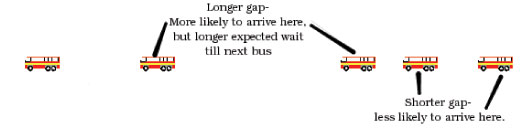
Imagem cortesia de Ben Parker
Quando chegamos à paragem, é provável que o tenhamos feito num período em que o intervalo entre chegadas é maior – um grande intervalo ocupa mais tempo do que um curto intervalo, pelo que é mais provável escolhermos o maior. Uma vez que nos calhou um intervalo grande, sabemos que este será superior a 12 minutos (circulam 5 autocarros por hora) – logo, o tempo médio de espera será superior a 6 minutos, uma vez que o nosso tempo de chegada tem a mesma probabilidade em qualquer momento do intervalo.
Isto é conhecido como o paradoxo da inspecção, e é complicado compreendê-lo. No entanto, é um fenómeno bem real usado por investigadores de planeamento e controlo de tráfego, responsáveis por descobrirem as formas mais eficientes de programar as filas em postos de correios, para depois as ignorarem completamente.
Será que as empresas de transporte estão erradas ao publicitarem que garantem um autocarro a, aproximadamente, cada 12 minutos? Eu penso que sim, embora seja difícil considerar todos os pormenores do paradoxo da inspecção; talvez neste caso possamos perdoar alguma falta de rigor estatístico.
Conclusões
Regra geral, a estatística é bastante intuitiva e são raros os casos difíceis de compreender. Um leitor atento deve:
- Descobrir quem apresenta a informação e quais os seus objectivos.
- Se possível, deve procurar qual o método de amostragem – verificar se os dados provêm de uma amostra representativa da população, e se os métodos são aplicados de forma justa. Existem comparações justas e imparciais? Será que a pergunta é coloca de forma correcta?
- Deve questionar qualquer média ou percentagem apresentadas e considerar quão extremas as estatísticas podem ser e o que seria de esperar para cada extremo. Principalmente, nunca deve assumir que os valores médios sejam os valores típicos.
As estatísticas são uma ferramenta útil e poderosa, quando lidadas correctamente, e devemos proporcionar ao público uma forma de as compreenderem. Também devemos assegurar nas escolas uma educação básica em estatística, particularmente na interpretação da publicidade. Até que os jornalistas, a indústria de marketing e as pessoas que a controlam, aprendam a apresentar dados estatísticos, as pessoas nunca estarão a comprar o melhor creme para a pele ou a melhor comida para os seus animais de estimação, principalmente porque possuem um número de orelhas superior à média

References
- DWP (2006) Households Below Average Income (HBAI) 1994/95-2004/05. London, UK: Department for Work and Pensions
- A primeira publicação deste artigo foi na revista Plus, uma revista online gratuita dedicada à divulgação da matemática: http://plus.maths.org. O artigo ‘Damn lies’ ficou em segundo lugar na edição de 2006 do prémio Plus para novos escritores.
Review
Este artigo apresenta uma visão humorística sobre a forma como a estatística é mal interpretada no nosso dia-a-dia. Deve ser facilmente compreendido por professores, estudantes e leitores em geral. No ensino, pode ser usado como uma introdução às noções de estatística e probabilidade, por forma a encorajar os alunos a criticarem a forma como a probabilidade e a estatística são usadas e abusadas.
Gosto particularmente dos cabeçalhos divertidos no artigo – às vezes óbvios, mas nem sempre.
Marco Nicolini, Itália





