Goede trillingen: hoe een gravitatiegolf te vangen Understand article
Vertaald door Roland Van Kerschaver en Erik Crampe. Gravitatiegolven behoren tot de bijna onmerkbaarste boodschappers die ons bereiken vanuit de kosmos. Maar hoe kunnen hun oneindig kleine effecten gedetecteerd worden?

zwarte gaten die naar elkaar
toe bewegen op een spiraal
vooraleer samen te smelten
en daarbij gravitatiegolven
vrij te maken.
Image courtesy of ESA / C
Carreau
In 2015 werden de fantastisch zwakke signalen van gravitatiegolven die de kosmos doorkruisten eindelijk gedetecteerd. Een eeuw voordien voorspeld door Albert Einstein, was deze eerste detectie van gravitatiegolven het hoogtepunt van tientallen jaren experimenteel en theoretisch werk – en ook het begin van een uitdagend nieuw tijdperk in de kosmologie.
Dus wat zijn gravitatiegolven en waarom was ze detecteren zo’n grote uitdaging? Gravitatiegolven zijn rimpels in de ruimte-tijd veroorzaakt door een versnellende massa. Feitelijk zijn ze het gravitatie equivalent van elektromagnetische golven – en net als die reizen ze met de lichtsnelheid.
De reden waarom die vluchtige signalen zo moeilijk te detecteren zijn is dat hun effecten zo uiterst, uiterst klein zijn: slechts een kleine vervorming in de ruimte-tijd, zelfs als de gebeurtenis die ze veroorzaakt zo groot is als de botsing van twee (veraf gelegen) zwarte gaten, zoals dit het geval was voor de waarnemingen van 2015. Deze vervorming betekent dat de afstand tussen twee punten op aarde uitgerekt of samengedrukt zal worden over een absoluut klein gedeelte van de afstand wanneer een gravitatiegolf voorbij passeert. En hier betekent ‘klein’ een factor van 10-21 (een duizend miljard miljardste) – ruwweg de diameter van een atoom vergeleken met de afstand tussen aarde en de zon: zeker een uitdaging om dit te meten!
Sinds begin 1960 zijn fysici, ingenieurs en technici van over de hele wereld hierop ingegaan, wat resulteerde in een handvol gigantisch grote instrumenten bestemd voor het detecteren van gravitatiegolven, waaronder LIGOw1 , Virgow2 en GEO600w3 . In dit artikel focusseren we ons op het Virgo toestel (terug te vinden in Italië), maar de concepten gelden eveneens voor de andere detectors – die allen deel uitmaken van een internationaal netwerk dat veel sterker is dan welke afzonderlijke detector ook. De analyse van de gegevens omvat in de eerste detecties werd in feite uitgevoerd door de samenwerking van wetenschappers van LIGO en Virgo.
Meten met licht
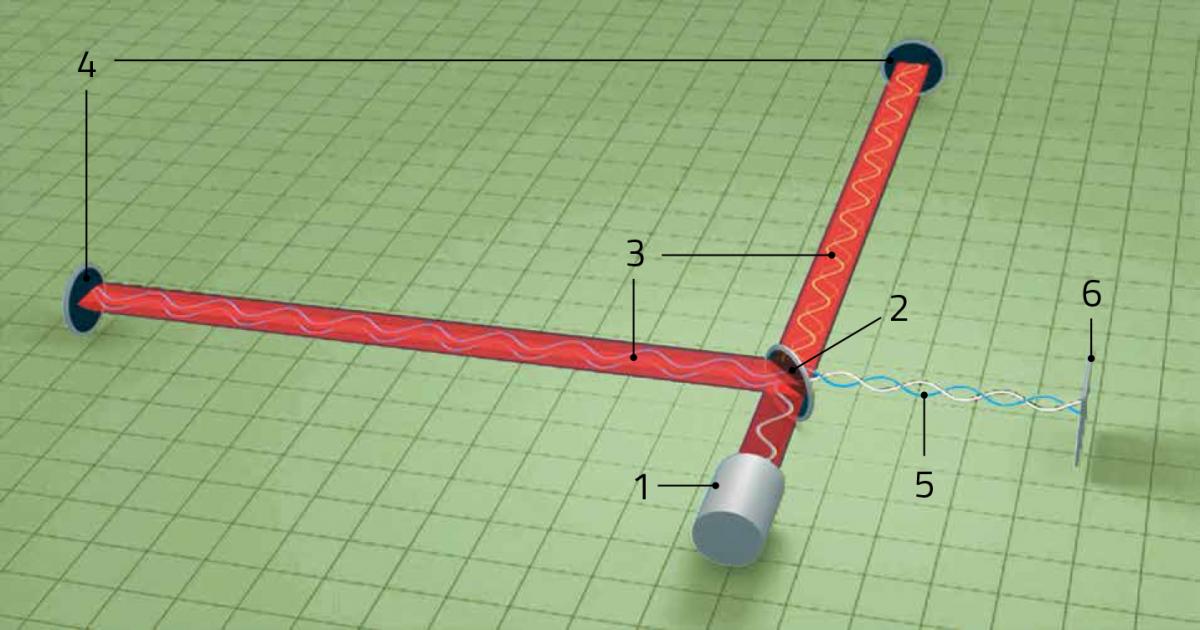
Het ontwerp van Virgo is gebaseerd op een toestel dat een interferometer van Michelson wordt genoemd, en dat zelf een opmerkelijke stamboom heeft: het werd voor het eerst gebruikt in 1887 door de fysici Albert Michelson en Edward Morley in een beroemd experiment om te zoeken naar veranderingen van de lichtsnelheid, veroorzaakt door de hypothetische ether (figuur 1).
Beeld ter beschikking gesteld door LIGO / T Pyle
Hier wordt licht van één bron opgesplitst in twee bundels die verder reizen langs loodrecht op elkaar staande banen (of ‘armen’) en daarna worden teruggekaatst door spiegels zodat ze uiteindelijk recombineren. Als er een verandering in lengte is van één van de banen van een bundel (zoals veroorzaakt kan worden door het passeren van een gravitatiegolf), dan zal de reistijd ervan zeer weinig veranderen, en dus een faseverschuiving veroorzaken van de ene bundel ten opzichte van de andere. Deze faseverschuiving beinvloedt de manier waarop de twee bundels zullen interageren wanneer ze elkaar ontmoeten bij hun terugkeer, en dat zal op zijn beurt een invloed hebben op het vermogen gemeten aan de uitgang van de detector.
Maar zelfs met dit klassiek ontwerp gecombineerd met moderne technologie, zullen de experimentele uitdagingen om gravitatiegolven te detecteren zeer groot zijn.
Virgo: de uitdagingen overkomen
In Virgo, is het basisontwerp van de interferometer van Michelson veel ingewikkelder gemaakt – en groter – omwille van de vereiste extreme stabiliteit en nauwkeurigheid.
Lange armen
Elke arm van de Virgo detector is 3 km lang. Deze grote omvang is nodig omdat de extreem kleine verandering van de reistijd van de bundels, veroorzaakt door de gravitatiegolf, toeneemt met de lengte van de armen. Lengten groter dan 3 km zijn niet echt mogelijk; een reden daarvoor is dat de kromming van de aarde dan een factor zou zijn waarmee rekening moet gehouden worden bij het bouwen van perfect rechte armen.
Om interacties te vermijden tussen de bundels fotonen en gasmoleculen, is het binnenste van de armen luchtledig gemaakt tot ongeveer een duizendste van een miljardste (10-12) van de atmosferische druk, vergelijkbaar met de druk in de ruimte op de hoogte van het Internationaal Ruimte Station (ISS). Dit maakt van de Virgo buizen het grootste ultrahoge-vacuüm volume in Europa (zie figuur 2). Op het einde van elke arm, wordt de wand van de buis afgekoeld tot cryogene temperaturen met vloeibare stikstof om restmoleculen (bijv. van water) te vangen.

Beeld ter beschikking gesteld door Cyril Fresillon / Virgo / CNRS Photothèque
Spiegels, spiegels
De spiegels in Virgo zijn een top component van de detector. Ze worden gemaakt met uiterste precisie: hun oppervlakken worden gepolijst tot ze perfect vlak zijn (tot op de naaste nanometer), en speciale coatings optimaliseren de manier waarop de spiegels licht terugkaatsen en doorlaten, de verliezen van de bundels op een minimum houdend (rond enkele deeltjes per miljoen). De opstelling van de spiegels is veel ingewikkelder dan bij een eenvoudige Michelson interferometer, met spiegels die gebruikt worden om bijkomende ‘optische caviteiten’ te vormen waardoor de bundel reist, of om de laserbundel te ‘reinigen’ (zie figuur 3).
De spiegels van Virgo spelen het ook klaar om de banen van de bundels langer te doen lijken dan ze zijn: een toestel dat een Fabry-Perot optische caviteit genoemd wordt, is geïnstalleerd in iedere arm om de baanlengte en de reistijden van de bundels met een factor van rond de 300 te doen toenemen, en dus ook de gevoeligheid van de gehele detector – met een zelfde factor.
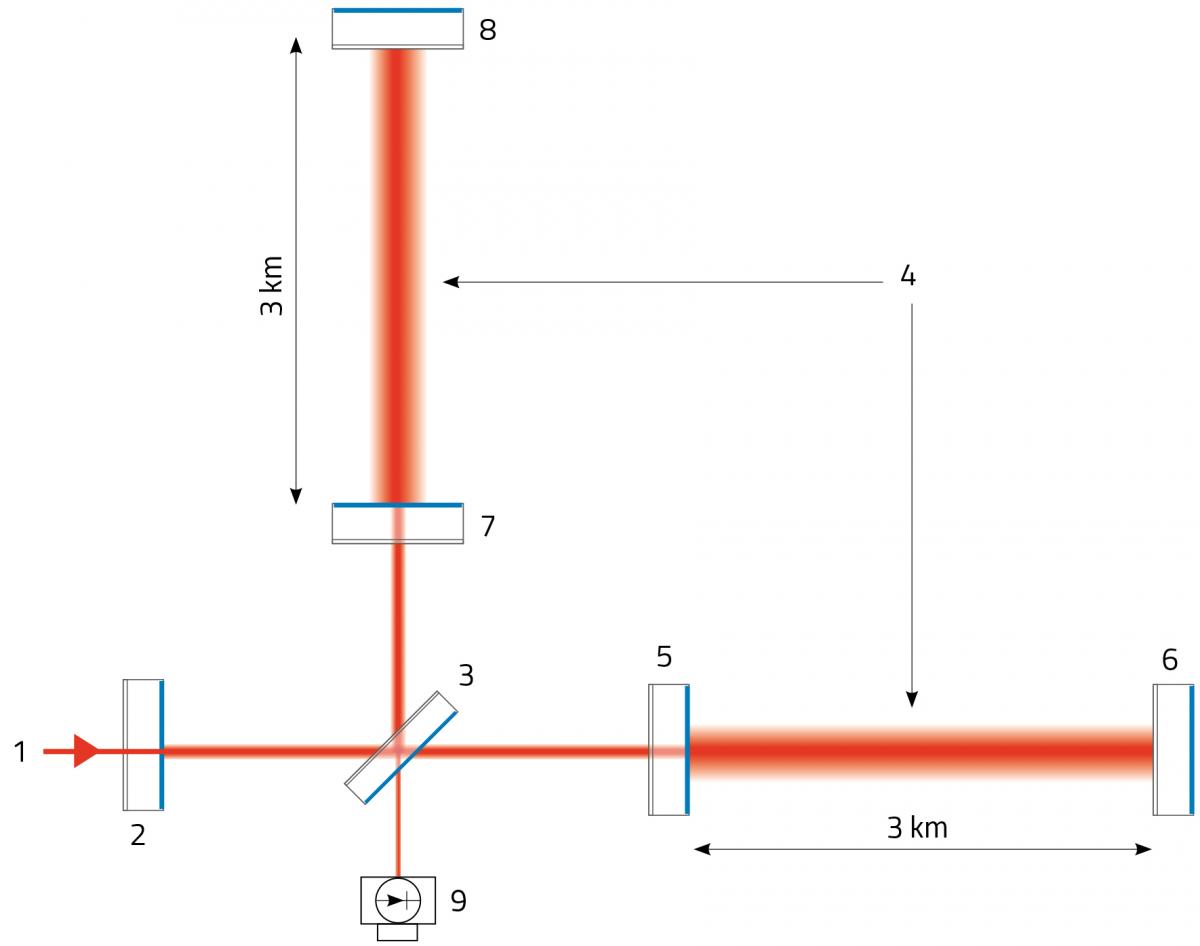
Beeld ter beschikking gesteld door The Virgo Collaboration
Isolatie tegen trillingen
Virgo moet gevoelig zijn voor de zeer kleine lengteveranderingen van de banen van de bundels veroorzaakt door gravitatiegolven, daarom moet het zoveel mogelijk geïsoleerd worden van andere storingen in de omgeving – menselijke activiteiten, wind, stormen en zo voort. Omdat het de bedoeling is van het ontwerp van de detector deze zoveel mogelijk af te schermen van zulke storingen, is een van de grootste problemen dat de spiegels (die de laserbundel weerkaatsen) vastgemaakt zijn aan de grond, die gans de tijd aan het bewegen is – veel te weinig dat wij het zouden voelen, maar heel wat meer dan de veranderingen te wijten aan de gravitatiegolven.
Dit betekent dat de spiegels geïsoleerd moeten worden van de grond – dat wordt in Virgo bereikt door iedere spiegel op te hangen aan het einde van een keten slingers die ‘super verzwakkers’ genoemd worden. Die maken van de eraan opgehangen spiegels ver weg de meest bewegingsloze voorwerpen op onze planeet (zie figuur 4). Maar hoe isoleert het ophangen van het voorwerp, dit voorwerp van trillingen?
Iedere eenvoudige slinger heeft zijn eigen natuurlijke of ‘resonantie’ frequentie – de frequentie waarbij het zal gaan slingeren bij de minste duw. Als we aan het bovenste van een slinger schudden met een frequentie lager dan de resonantiefrequentie, dan zal van de slinger het uiteinde onderaan bewegen. Maar als de ingevoerde beweging een hogere frequentie heeft dan de resonantie, dan zal het onderste uiteinde nagenoeg stil blijven. In Virgo, hebben de slingers die de spiegels dragen resonantiefrequenties die zo laag mogelijk zijn (enkele hertz). Dit betekent dat ze niet verstoord worden door bewegingen bij hogere frequenties, zodat gravitatiegolven met een frequentie boven enkele tientallen hertz kunnen gedetecteerd worden.
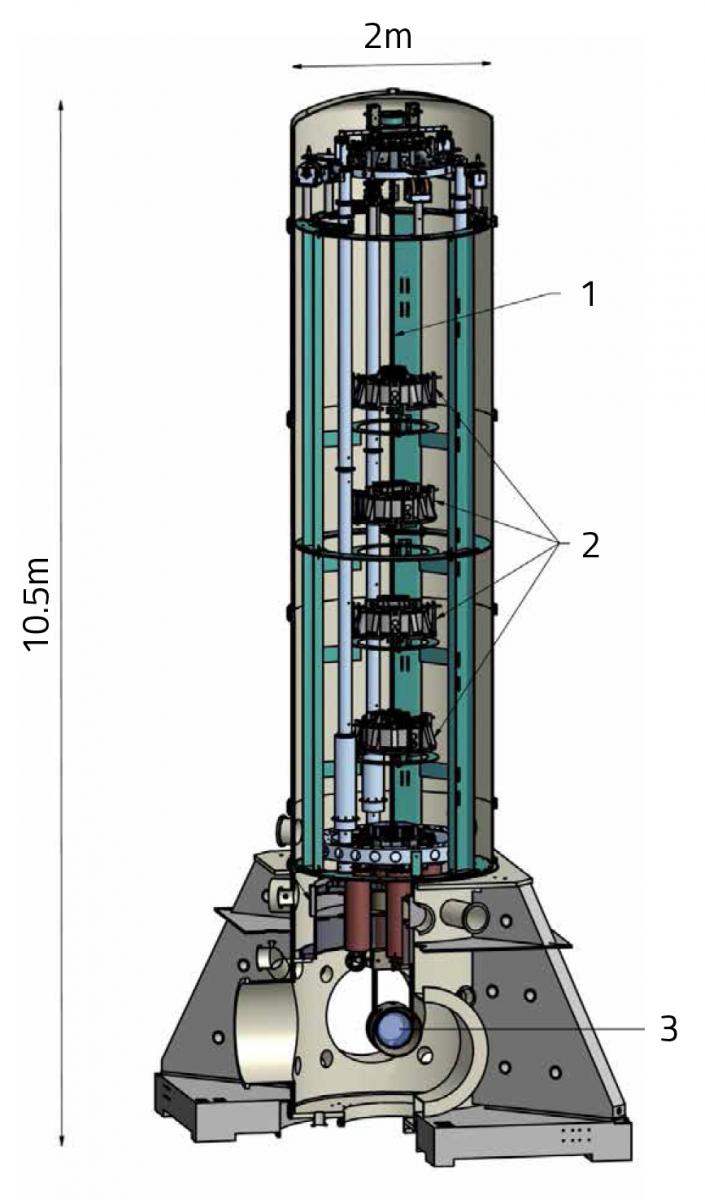
1: draad van slinger; 2: keten slingers; 3: spiegel
Beeld ter beschikking gesteld door The Virgo Collaboration
Het behouden van de nauwkeurigheid
Om gevoelig te zijn voor gravitatiegolven wanneer ze ook maar aankomen, moet Virgo voortdurend in een zeer precies gecontroleerde werktoestand gehouden worden. De laserbundel (een infrarode laser met een golflengte van 1064 nm) moet bijvoorbeeld ultra stabiel gehouden worden om een constant vermogenniveau te behouden aan de uitgang van de detector. De frequentie van de laser moet ook gestabiliseerd worden zodat het minder dan 1 deel op 1014 verandert.
Sondes geplaatst over de hele lengte van het Virgo toestel gaan voortdurend de toestand ervan na en laten toe dat de lengtes van optische caviteiten gecontroleerd worden op het niveau van de femtometer (10-15 m), terwijl de fout op de hoek waarover de spiegel is gericht tot enkele nanoradialen (minder dan een een miljoenste van een graad) beperkt is. Bovendien houden duizenden sondes de omgeving en de toestand van Virgo in het oog. Dit levert data die kunnen gecontroleerd worden van zodra een mogelijke gravitatiegolf waargenomen wordt.
Meer te weten komen
Er is veel meer uit te leggen over het Virgo experiment – bijvoorbeeld, hoe de data geanalyseerd worden om te weten te komen of er werkelijk een gravitatiegolf gedetecteerd is. Als je meer wil weten, bezoek dan onze websitew2 of lees het het recent artikel in Science in School dat beschrijft hoe gravitatiegolven voor het eerst werden gedetecteerd (Kwon, 2017) – en de ontdekkingen die deze nieuwe mogelijkheid kunnen betekenen voor de astrofysica.
Bedanking
De auteur wenst Dan Hoak (van het Europees Observatoriun voor Gravitatie) te danken voor zijn hulp bij het voorbereiden van dit artikel.
References
-
Voor een eerder in Science in School verschenen artikel over het detecteren van gravitatiegolven, zie:
-
Kwon D (2017) Zet die kosmische micro aan. Science in School 39.
-
Web References
-
w1 – The Laser Interferometer Gravitational-Wave Observatory (LIGO) bevindt zich in de VSA.
-
w2 – Tref meer informatie over Virgo op de Virgo website.
-
w3 – GEO600 is een op de grond geplaatste interferometrischc detector voor gravitatiegolven die zich bevindt bij Hannover, Duitsland.
Resources
-
Om te weten te komen hoe de Virgo detector werkt, bekijk deze korte animatie.
-
Bekijk de persconferentie waarop de detectie van de eerste gravitatiegolf aangekondigd werd.
-
Verneem meer over het LIGO Open Science Center, met inbegrip van data van de detecties in 2015.
-
De LIGO-Virgo samenwerking heeft zijn eigen YouTube kanalen met spreekbeurten, lessen en instructievideos.
-
Verneem meer over gravitatie en gravitatiegolven van een animatie en strip in verschillende talen, gemaakt door PhD Comics.
Review
Dit artikel beschrijft de werking van detectors van gravitatiegolven – grote maar zeer gevoelige machines die leerlingen zeer interessant kunnen vinden. De details van hoe die machines werken, en de problemen die moesten worden opgelost om hun grote nauwkeurigheid te bereiken, worden op een zeer begrijplijke manier beschreven door de auteur, die een wetenschapper is die gravitatiegolven onderzoekt.
Enkele denkvragen zouden kunnen zijn:
- Wat zijn gravitatiegolven?
- Waarom is het zo moeilijk om gravitatiegolven te detecteren?
- Hoe werken gravitatiegolf detectors?
- Gravitatiegolf detectors zijn zeer gevoelige sensors. Waarom zijn die machines zo groot?
- Het bouwen van gravitatiegolf detectors is een echte uitdaging. Beschrijf de belangrijkste moeilijkheden en hoe ze kunnen opgelost worden.
Gerd Voght, Hogere Secundaire School voor Milieu en Economie, Oostenrijk





