Een proef voor in je klas: het meten van de constante van Planck Teach article
Vertaald door Roland Van Kerschaver. Breng het ontdekken tot leven in je klas en toon je leerlingen hoe je de constante van Planck kan bepalen met eenvoudige toestellen.

Akimbomidget/Wikimedia
Wanneer we eraan denken fysische constanten, zoals de lichtsnelheid of de gravitatiekracht, te bepalen dan hebben we het waarschijnlijk over beroemde grootschalige experimenten – maar je kan met de uitrusting in je klas zulke constante ook bepalen.
De constante van Planck is voor de leerlingen wellicht wereldvreemd in tegenstelling tot de lichtsnelheid, maar speelt een centrale rol bij het begrijpen van het gedrag van de materie op subatomair niveau. Het is een hoeksteen van de quantummechanica, dat daar het vreemde gedrag beschrijft van deeltjes. De energie bestaat dan zoals materie uit deeltjes. Licht en andere elektromagnetische stralingw1, bestaat uit deeltjes die fotonen genoemd worden.
Figuur in het Publiek Domein
Figuur/Wikimedia
Genoemd naar de Duitse natuurkundige Max Planck (1858-1947), leert de constante van Planck ons hoe de energie van de fotonen in verband staat met de golflengte, zoals volgende belangrijke vergelijking ons laat zien:
Ep = hc/λ
Daarbij is Ep de energie van een enkel foton (in joule), h de constante van Planck, c de lichtsnelheid in het luchtledige en λ de golflengte van de straling.
Verbazend gezien de constante van Planck zo onwaarschijnlijk klein is dat we die kunnen bepalen met een proef die kan uitgevoerd worden in je klas. Die proef vereist geen speciaal materieel – slechts enkele diodes die gekleurd licht uitzenden (LEDs) en verder gewone elektrische toestellen. Deze activiteit is geschikt voorleerlingen vanaf een leeftijd van ongeveer 16 jaar.
Hoe een LED werkt
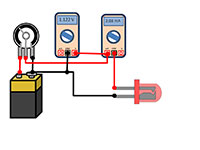
het meten van de spanningen
en bijhorende
stroomsterkten van een LED.
Van links naar rechts: batterij
met potentiometer,
voltmeter, ampèremeter en
LED.
Figuur met dank aan de
auteurs
LEDs worden gemaakt door het samenvoegen van twee ‘gedopeerde’ halfgeleiders. De ene heeft een overschot aan elektronen (n-type) en de andere een tekort eraan, dus teveel gaten (p-type). Wanneer een elektrische stroom door de ‘p-n’ junctie loopt, wordt bij het recombineren van elektronen en gaten energie vrijgemaakt in de vorm van fotonen.
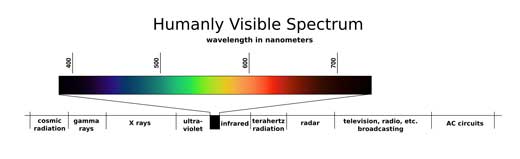
De kleur van het licht uitgezonden door een LED wordt bepaald door de energie van de fotonen. LEDs bestaan gewoonlijk uit legeringen van aluminium, silicium en arseen waarbij het op maat veranderen van de proportionele chemische samenstelling van het halfgeleidermateriaal LEDs geeft die licht van bepaalde kleuren uitzenden – zoals rood en groen in het zichtbaar gedeelte van het elektromagnetisch spectrum, of erbuiten in het ultraviolet en infrarood gebied.
De golflengte van licht bepaalt zijn kleur. Het menselijk oog is gevoelig voor licht met golflengten tussen ongeveer 390 nm en 700 nm (nanometer). Violet heeft de kortste golflengte en rood de langste, en iedere golflengte ertussen komt overeen met een bepaalde kleur in het spectrum. Bijvoorbeeld zal een LED die groen licht uitzendt licht geven met een golflengtevan rond de 567 nm.
We gebruiken LEDs in deze proef omdat iedere kleur een verschillende spanning heeft waarbij elektronen beginnen te stromen.Het meten van die spanningen, samen met de golflengten van het uitgezonden licht, maakt het ons mogelijk de constante van Planck te bepalen.
Materialen
- Vier LEDs die gekleurd licht uitzenden – rode, oranje, groen en blauw. Kies LEDs met een doorzichtig kleurloos omhulsel, zodat de kleur van het licht afkomstig is van de LED zelf en niet van het gekleurd omhulsel.
- Een batterij van 9 V.
- Twee multimeters (de ene gebruikt als voltmeter, de andere als ampèremeter).
- Een potentiometer van 1 kΩ.
Werkwijze
- Maak de schakeling zoals in het diagram. Verbindt de ampèremeter in serie met de LED om de stroomsterkte erdoor te meten, en de voltmeter in parallel met de LED om de spanning erover te meten. De aangelegde spanning kan veranderd worden met een potentiometer.
- Verander de spanning in stappen van 0,05 V van 0 V tot 3 V, en meet de elektrische stroomsterkte. Merk op dat wanneer de stroom die door de LED loopt klein is, deze mogelijk geen licht geeft, maar wel reeds af te lezen is op de ampèremeter. De stroomsterkte door de LEd mag niet groter worden dan 5 mA.
- Teken een grafiek van stroomsterkte in functie van spanning voor elke LED, zoals grafieken hiernaast. Vindt voor elke grafiek de rechte die het best past bij de punten die een helling vormen vanaf d x-as. Liggen die punten dicht bij de rechte, dan is er een lineair verband tussen de spanning en de stroomsterkte in dit gebied van de grafiek.
- Nu bepalen we de activatiespanning (Ua) uit de verzamelde gegevens. Dit is het punt waarop de stroomsterkte lineair begint toe te nemen met de spanning. Dit is af te lezen op de grafiek door de rechte te extrapoleren van boven naar beneden tot in het punt waar de x-as gesneden wordt. De leerlingen kunnen dit op het zicht doen met een lat, of door de lineaire regressie toe te passen op de experimentele gegevens in het lineair gebied w2.
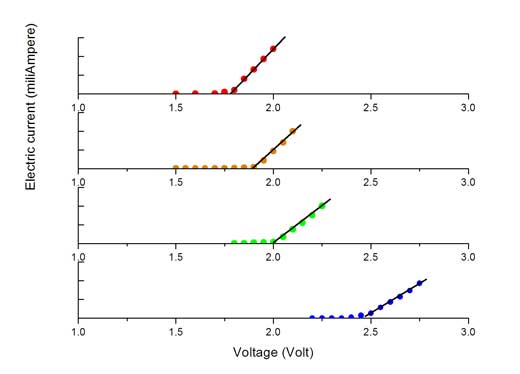
Figuur met dank aan de auteurs
Om de nauwkeurigste waarden voor Ua voor iedere kleur te bekomen, kan je het gemiddelde nemen van de resultaten van verschillende leerlingen.
Typische waarden bekomen voor de met deze proef bekomen activatiespanningen zie je hiernaast, tesamen met de golflengten uitgezonden door de LEDs. Je kan aan de leerlingen die golflengten opgeven. Als alternatief, kunnen de golflengten gemeten worden met een zelfgemaakte spectrometer, zoals deze beschreven in een vroeger verschenen artikel in Science in Schoolw3.
| Kleur van LED | Typische golflengte, λ (cm) | Activatiespanning, Ua (V) |
|---|---|---|
| Rood | 623 | 1.78 |
| Oranje | 586 | 1.90 |
| Groen | 567 | 2.00 |
| Blauw | 567 | 2.45 |
Figuur met dank aan entirelysubjective/Flickr
Analyse en resultaten
De energie van de uitgezonden fotonen, Ep (gemeten in joule),is in verband te brengen met de constante van Planck (h), de lichtsnelheid in het luchtledige (c), en de golflengte van het licht λ:
Ep = hc/λ (1)
In dit experiment hebben we een bereik van waarden voor ? voor het gekleurd licht van de LEDs, en we kennen de waarde voor c (2,9979 x 108 ms-1). Maar hoe gebruiken we de bekomen waarden van Ua om de constante van Planck te berekenen? Om dit te vinden, bekijken we wat er gebeurt binnenin de LEDs.
Wanneer een LEDs aangesloten is op een lage spanning, is de toegevoerde energie niet voldoende om fotonen te maken en is de elektrische stroom zeer klein. Bij de activativatiespanning Ua licht de LED op. Deze kleinste spanning komt voor iedere kleur van een LED overeen met de energie van de uitgezonden fotonen, Ep. En het is nu zo dat er voor Ua zoals voor Ep een verband is met de constante van Planck en de golflengte van het uitgezonden licht, zoals getoond in de volgende vergelijking:
Va = Ep/e + φ/c (2)
Hierbij is e de lading van een elektron (1,6022 x 10-19 coulomb). Voor spanningen groter dan Ua wordt de elektrische stroom bepaald door de inwendige weerstand van de LEDs. Uit de wet van Ohm, spanning = weerstand x stroomsterkte, volgt een lineair verband tussen de elektrische stroom en de aangelegde spanning, zoals te zien in de spanning-stroomsterkte karakteristieken.

halfbollen op de oever van de
Zwaan Rivier in Perth, West
Australië.
Figuur met dank aan
Gnangarra/Wikimedia
In de vergelijking 2, is (φ/c) een constante in verband met de energieverliezen binnen de p-n junctie van de halfgeleider. Om het eenvoudig te houden, nemen we aan dat die constant is voor al de LEDs. Omdat φ onbekend is, is het onmogelijk de constante van Planck te bepalen alleen door het meten van de activatiespanning. Als evenwel de activatiespanning gemeten wordt voor enkele LEDs die licht uitzenden met gekende golflengte, dan kunnen we hvinden als we de grafiek tekenen van Ua in functie van de omgekeerde van de golflengte (1/λ).
Dit is zo omdat een herschikking van (2) volgende vergelijking geeft:
Ua = hc/e(1/λ) + φ/c (3)
Zo zal de grafiek van Ua tegen 1/λ de vorm aannemen van een rechte lijn met helling hc/e waaruit h gemakkelijk kan berekend worden, gezien de waarden van e en c gekend zijn. Die helling kan grafisch gevonden worden door het tekenen van een rechte die best past bij de gegevens, of gebruik te maken van een rekenmachine met lineaire regressiew2.
Lineaire regressie geeft de volgende waarde voor de hellin: hc/e = 1,24811 x 10-6 V.m. Hieruit kan de constante van Planck eindelijk worden berekend:
h = em/c (4)
= 1,6022 x 10-19 x 1,24811 x 10-6/2,9979 x 108
= 6,6704 x 10-34 J.s
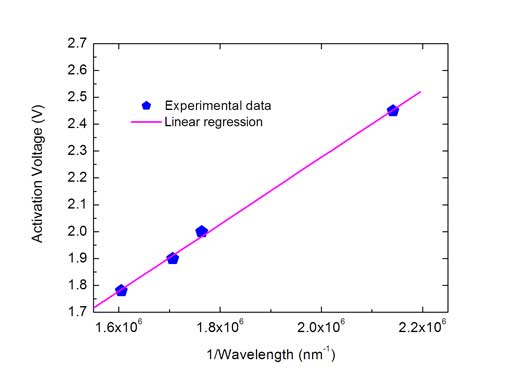
Figuur met dank aan de auteurs
Deze waarde stemt overeen met de aanvaardde waarde voor de constante van Planck van 6,62606957 x 10-34 Js – de fout draagt 0,7 procentw4. De waarden die je leerlingen bekomen kunnen een iets grotere fout hebben, maar zijn toch een vrij goede benadering voor een van de fundamentele natuurconstanten.
Web References
- w1 – Om meer te leren over licht en het elektromagnetisch spectrum:
- Mignone C., Barnes R. (2011) More than meets the eye: the electromagnetic spectrum. Science in School 20:51-59.
- w2 – Online lineaire regressie calculators die je gegevens kunnen helpen analyseren:
- w3 – Om te leren hoe je eigen spectrometer te maken:
- Tiele Westra M. (2007) A fresh look at light: build your own spectrometer. Science in School 4:30-34.
- w4 – De standaard waarde voor de constante van Planck van het NIST (National Institute of Standards and Technology).
Resources
- In een video van het ‘Zestig Symbolen’ project van de Universiteit van Nottingham wordt het belang van de constante van Planck uitgelegd.
Review
Dit artikel gaat over een eenvoudig experiment waarmee de constante van Planck gemakkelijk kan bepaald worden. Deze wordt veel gebruikt in de quantumfysica. Het opstellen van deze proef lukt altijd in klas, gezien de benodigheden die gebruikt worden te vinden zijn in ieder fysicalab. Deze proef kan gebruikt worden als demonstratie in de klas of voor onderzoek uitgevoerd door de leerlingen zelf.
De theorie waarover het gaat kan aanvankelijk abstract lijken voor de leerlingen en moeilijk te verstaan, maar zulk experiment helpt hen bepaalde concepten te verhelderen en de theorie waarover het gaat beter te verstaan. Het artikel en het experiment demonstreert enige zeer belangrijke concepten, zoals:
- het foto-elektronisch effect, waarbij ‘energiepakketten’ opgeslorpt worden door een diode waardoor die elektromagnetische golven uitgezendt;
- de activatiespannning van diodes;
- het berekenen van de constante van Planck.
Catherine Cutajar, Malta





