Modeleren van de verandering van het klimaat in de klas Teach article
Vertaald door Roland Van Kerschaver. Waarom zou je je leerlingen er niet toe bewegen om hun eigen voorspellingen te doen over de verandering van het klimaat - met de hulp van Dudley Shallcross en Tim Harrison van de Universiteit van Universiteit van Bristol (in het Verenigd Koninkrijk)?
Klimaatverandering en opwarming van de aarde zijn “warme” onderwerpen en verdienen dan ook een belangrijke plaats in het wetenschappelijk curriculum van iedere school. Maar hoe voorspellen we hoe ons klimaat zal veranderen? Het is nodig om de leerlingen een eenvoudige inleiding te geven op het modeleren van het klimaat. In dit artikel tonen we aan dat leerlingen gebruik kunnen maken van een doodgewoon werkblad om de voornaamste factoren die een invloed hebben op het klimaat van de aarde te onderzoeken.
Een eerste poging om het klimaat te modeleren
Het eenvoudigste model van het klimaat is er een waarin de binnen-komende energie van de zon gelijk is aan de buitengaande energie uitgestraald door de aarde, met andere woorden een “energie in” is gelijk aan “energie uit” model. We weten uit metingen dat het vermogen van de zon dat de bovenkant van de atmosfeer bereikt (per seconden), dit is de zonneconstante S, 1370 Wm-2 bedraagt.
We willen de gemiddelde temperatuur TA aan het oppervlak van de aarde berekenen. Als RA de straal van een perfect bolvormige aarde is, kunnen we met dit zeer eenvoudig model laten zien dat de aarde zonnestraling absorbeert op een oppervlakte πRA2 (van een cirkel) en straling emitteert uit een oppervlakte 4πRA2 (van een bol).
Hoe gaan we te werk?
(a) Energie in = energie uit
De wet van Stefan-Boltzmann (zie kader achteraan):
(b) Opgeslortp vermogen per oppervlakte-eenheid per tijdseenheid x totale opervlakte(cirkel) = uitgestraald vermogen per oppervlakte-eenheid per tijdseenheid x totale opervlakte(bol)
(c) 1370 x πRA2 = σTA4 x 4πRA2
Hieruit volgt:
σTA4 = 1370 = S/4
4
TA4 = 1370
(4 x 5,67 x 10-8)
TA = 279 K (6 °C)
waarbij σ de constante van Stefan-Boltzmann is (5,67 x 10-8 Wm-2K-4).
Op het eerste zicht lijkt dit een aanvaardbare waarde voor dit ruw model. We weten echter dat de gemiddelde temperatuur van de aarde nu 16 °C bedraagt. (Om daar iets aan te doen kunnen we de aarde verdelen in horizontale banden, gebruik te maken van de gemiddelde temperatuur van de verschillende banden en ze op te tellen en er het gemiddelde van te nemen). Wat er verkeerd is met dit zeer eenvoudig model is dat een deel van de zonne-energie niet geabsorbeerd wordt door de aarde, maar teruggekaatst wordt naar de ruimte door wolken en ijs.
Ongeveer 24% van de binnenkomende energie wordt teruggekaatst door de wolken en een ander 6% wordt teruggekaatst door het ijs. Dit geeft een totaal terugkaatsend vermogen van de aarde – dit is de albedo factor (A) – van 30% of 0,3. Daarom moet de linkerkant van Vergelijking (c) herschreven worden als 0,7 x 1370 x πRA2 en kunnen we TA opnieuw berekenen:
TA4 = 1370 x 0,7
(4 x 5,67 x 10-8)
TA = 255 K (-18 °C)
Deze waarde is blijkbaar nog lager, en dat leidt natuurlijk tot de vraag: waarom is de aarde zo warm? Om een antwoord te geven op die vraag hebben we een nog iets meer ingewikkeld model nodig.
Essentiële achtergrond fysica
Straling van een zwartlichaam en de wet van Stefan-Boltzmann
Alle lichamen stralen energie uit in de vorm van elektromagnetische straling. Een zwart lichaam absorbeert al de straling die erop valt. Het zendt straling uit in functie van de temperatuur van zijn oppervlak.De wet van Stefan-Boltzmann geeft de totale energie I, uitgestraald door een zwart lichaam bij gelijk welke temperatuur, T, met de formule:
I(T) = σT4 (Vergelijking 1)
Daarbij is:
I de energie per eenheid van oppervlakte uitgezonden per seconde (Wm-2)
T de absolute temperatuur (K)
σ de constant van Stefan-Boltzmann (5,67 x 10-8 Wm-2K-4).
Model van de aarde met een atmosfeer bestaande uit één laag
Als we aannemen dat de atmosfeer bestaat uit één enkele laag mengbare gassen, kunnen we een meer nauwkeurig model maken. De leerlingen kunnen dat model gebruiken in een rekenblad. In dat model, wordt rekening gehouden met de absorptie door de atmosfeer van het inkomend zichtbaar en ultraviolet licht van de zon en de absorptie van het uitgaande infrarood licht uitgezonden door de aarde.
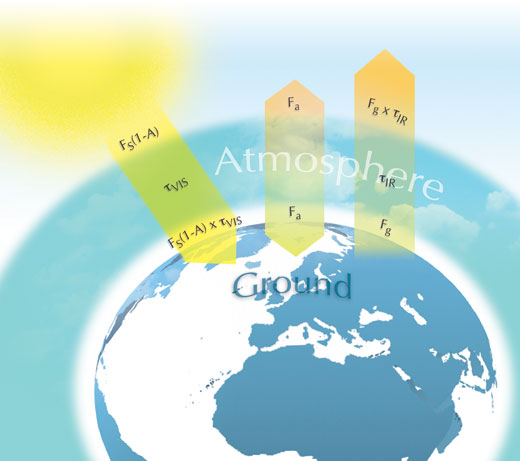
De figuur hieronder vat al de elementen van het model samen. FS is de zonneconstante gedeeld door 4 (S/4) omdat het inkomend vermogen terecht komt op een cirkel met oppervlakte πr2en het uitgaand vermogen uitgestraald wordt door een bol met oppervlakte 4πr2 (dat namen we reeds aan voor het eerste model). Het inkomend vermogen per m² van de zon bedraagt dan FS(1-A), waarbij A de albedo factor is – het deel teruggekaatst naar de ruimte. Dit inkomend vermogen per m² ligt in het ultraviolet en zichtbaar gebied van het spectrum van het licht. τVIS is het deel van dit inkomend vermogen per m² dat niet geabsorbeerd wordt door de atmosfeer. Als de atmosfeer alles absorbeert is τVIS = 0. Als de atmosfeer niets absorbeert is τVIS = 1. Het vermogen per m² dat het oppervlak van de aarde bereikt is: FS(1-A) x τVIS.
De aarde gedraagt zich als een zwarte straler en zal het vermogen per m² Fg uitzenden van op de grond (het oppervlak van de aarde). Dit uitgestraald vermogen per m² van de aarde ligt in het infrarood gebied van het spectrum van het licht. Bepaalde gassen in de atmosfeer absorberen infrarode stralen (broeikasgassen). τIR is het gedeelte van het infrarode vermogen per m² dat niet geabsorbeerd wordt door die gassen in de atmosfeer, en is het uitgaande vermogen per m²: Fg x τIR.
We nemen aan dat het vermogen per m² van de atmosfeer Fa is en dat de energie in en uit aan het oppervlak van de aarde en de bovenkant van de atmosfeer allebei in evenwicht zijn.
Aan de oppervlakte van de aarde:
FS(1-A) x τVIS + Fa = Fg (Vergelijking 2)
Aan de bovenkant van de atmosfeer:
Fg x τIR + Fa = FS(1-A) (Vergelijking 3)
We combineren de vergelijkingen 2 en 3:
Fg = FS(1-A)(1 + τVIS)
(1 + τIR)
We halen de wet van Stefan-Boltzmann er terug bij:
Fg = σTA4 = FS(1-A)(1 + τVIS)
(1 + τIR)
TA = [ FS(1-A)(1 + τVIS) ]0,25
[ σ(1 + τIR) ] (Vergelijking 4)
Als we de volgende waarden nemen voor de parameters:
FS = 1370/4 = 342,5 Wm-2 (zonneconstante gedeeld door 4)
A = 0,3
τVIS = 0,8
τIR = 0,1
geeft Vergelijking 4 ons:
TA = 288,5 K (15,5 °C),
En dat is toch wel de huidige gemiddelde temperatuur aan het oppervlak van de aarde en we zijn dan ook tevreden over ons model.
De Vergelijking 4 kan in een programma zoals Microsoft Office Excel 2007 aangebracht worden zodat de leerlingen kunnen nagaan wat de veranderingen van de temperatuur van de aarde zijn wanneer de waarden van de parameters A, τVIS en τIR van de Vergelijking 4 veranderd worden. Dit werd gedaan en een interactieve versie ervan kan online gebruikt of ingeladen worden van de websitew1 van de Universiteit van Bristol.
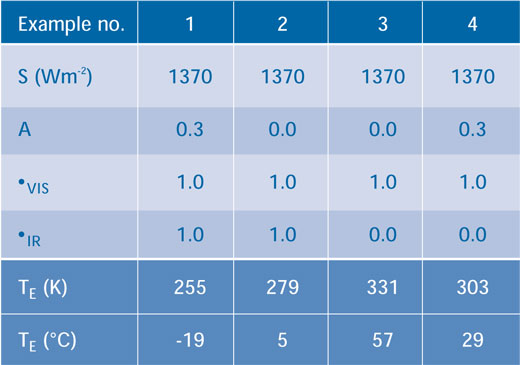
Tabel 1 toont voorbeelden van de uitvoer als de parameters A, τVIS en τIR veranderd worden. In Voorbeeld 1 nemen we aan dat de atmosfeer niets absorbeert van het binnenkomende of buitengaande vermogen per m² (zowe τVIS als τIR zijn dan gelijk aan 1,00) en de albedo is 0,30, wat een temperatuur geeft van 255 K (-19°C). In Voorbeeld 2, nemen we aan dat er geen wolken of ijs zijn (A = 0,00), wat de temperatuur van de aarde doet stijgen tot 279 K (5°C), hetgeen het belang van de albedo aantoont. In Voorbeeld 3, zijn er ook geen wolken of ijs (A = 0,00) maar de atmosfeer absorbeert al de uitgaande infrarode straling (IR = 0,00) en de aarde warmt op tot 331 K (57°C). Als we nu terug wolken en ijs invoeren in Voorbeeld 4 (A = 0,30), vermindert de temperatuur tot 303 K (29°C).
Mogelijke vragen
Vragen die gesteld kunnen worden, en waarvoor de leerlingen dit model zouden kunnen gebruiken, zijn:
- Welk van de veranderlijken heeft het grootste effect op de gemiddelde temperatuur van de aarde?
- Als de gemiddelde afstand tussen aarde en zon zou toenemen met 1% van de huidige waarde, zou de zonneconstante verminderd worden met een factor 1,0201, zodat deze 1343 Wm-2 zou worden. Hoeveel zou de temperatuur dan zijn? Neem een albedo van 0,30, τIR van 0,30 en τVIS van 0,60.
(De zonneconstante wordt geschaald met het kwadraat van de afstand, zodat de aarde 10% dichter bij de zon brengen zou betekenen dat S = 1370/(0,9)2 = 1691 Wm-2 en het verwijderen van de aarde met 1% zou betekenen dat S = 1370/(1,01)2 = 1343 Wm-2).
Natuurlijk kunnen er ook meer tot de verbeelding sprekende vragen gesteld worden.
We nemen aan dat het zand in de Sahara kan veranderd worden in een spiegel (zand kan gesmolten worden tot glas).
- Hoe groot zou die spiegel moeten zijn om de aarde 1 °C af te koelen?
- Hoeveel procent van de Sahara is dat?
Een meer gesofistikeerd model
Hoe doet ons eenvoudig model het vergeleken met een gesofistikeerd model zoals het Hadley Centrum klimaatmodel dat gebruikt wordt door de Meteorologische Dienst van het Verenigd Koninkrijk (zie beelden achteraan)? In feite gelijken de twee modellen erg op elkaar, afgezien van het feit dat het Hadley Centrum klimaatmodel de atmosfeer niet beschouwd als één laag, maar deze opsplitst in een aantal balken afhankelijk van hoogte, breedte- en lengteligging. Voor elke balk, berekent het model onmiddellijk de hoeveelheid binnenkomende ultraviolette en zichtbare straling die wordt uitgestraald en verstrooid binnen die balk, en de hoeveelheid infrarode straling uitgestraald door die balk, rekening houdend met de concentratie van de broeikasgassen en de oppervlakken van wolken en ijs. De meest gesofistikeerde versies van het Hadley Centrum klimaatmodel houden ook rekening met de warmtestroming in en uit de oceanen en de opname van CO2 door de vegetatie. Maar als je het principe van het eenvoudig model beet hebt, ben je goed op weg om de meer ingewikkelde echte klimaatmodellen door te hebben.
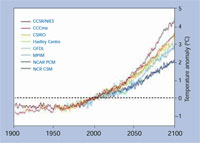
De voorspellingen van het
klimaatmodel voor de globale
opwarming betreffende de
gemiddelde temperatuur in 2000.
De gegevens van het gebruikte
model komen van het
Intergouvermentaal Paneel over
Klimaatverandering
Gegevensverspreiding Centrum.
Klik op de afbeelding om te vergroten.
Figuur met dank aan Robert A.
Rohde; bron: Wikimedia Commons
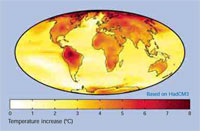
2070-2100 voorspelling vs.
1960-1990 gemiddelde. De kaart
van de voorspelde globale opwarming
op het einde van de 21ste eeuw.
Dit model vertoont een gemiddelde
opwarming van 3,0°C en maakt
gebruik van het Hadley Centrum
HadCM3 klimaatmodel. Klik op
de afbeelding om te vergroten.
Figuur met dank aan Robert A.
Rohde; bron: Wikimedia Commons
Deelnemen aan een echte simulatie van het klimaat
Climateprediction.netw2 is het meest grootschalig experiment om een voorspelling van het klimaat van de 21ste eeuw te maken. Dit wordt mogelijk door de hulp in te roepen van deelnemers van over gans de wereld die tijd op hun computer ter beschikking stellen als hun computer ingeschakeld is maar niet gebruikt wordt op z’n volle capaciteit. Het volledig klimaatmodel heeft vele parameters die bijgesteld kunnen worden. Om al die parameters te onderzoeken, moet een fenomenaal aantal simulaties worden uitgevoerd. Zelfs met de computers waarover het team van climateprediction.net beschikt, zou dat aantal simulaties zeer veel tijd in beslag nemen. Het idee achter climateprediction.net is dat iedereen een versie van het model kan inladen dat één van die vooraf vastgelegde parameters kan onderzoeken. Het model zal ongeveer drie maanden in de achtergrond van je computer aan het rekenen zijn terwijl je op je computer werkt, zonder dat je computer minder snel zal zijn. Je hebt er dan ook geen hinder van.
Er worden berekeningen uitgevoerd in drie delen. In het eerste deel worden berekeningen gedaan met gegeven van de jaren 1850 tot 1900. De bekomen voorspellingen worden vergeleken met de waargenomen temperaturen. Dat is nodig om het model te kalibreren. In het tweede deel gaat de simulatie over de periode van 1901 tot vandaag. In het derde deel houdt de simulatie het bij het klimaat in de toekomst (2000-2100) waarbij één parameter veranderd wordt. Eens dat de berekeningen klaar zijn, worden de gegevens automatisch opgeladen door de Meteorologische Dienst van het Verenigd Koninkrijk van zodra je computer verbonden is met internet. De gratis bezorgde software van de simulatie geeft de computergebruiker een grafiek met de veranderingen van het klimaat, zoals die berekend zijn. Temperatuurveranderingen per seizoen in functie van hoogte, breedte- en lengteligging zijn slechts enkele van de veranderlijken die kunnen zichtbaar gemaakt worden. Dit maakt het mogelijk een vakoverschrijdend project voor aardrijkskunde/ biologie/chemie/ fysicaop te starten op je school.
In het volgend nummer van Science in School, zullen de auteurs enkele chemieproeven voorstellen die relevant zijn wat betreft de verandering van het klimaat.
Web References
- w1 – Een interactieve versie van het eenvoudig klimaatmodel kan online gebruikt worden of ingeladen op volgende website: www.chemlabs.bris.ac.uk/outreach/resources/simple_climate_model/index.html
- Gebruik de glijders om de parameters te veranderen.
- w2 – Voor meer details over het experiment en hoe eraan deel te nemen, ga naar volgende website: http://climateprediction.net.
- De website van climateprediction.net geeft ook informatie en bronnen speciaal voor scholen, zowel in het Engels als het Spaans beschikbaar: http://climateprediction.net/content/resources-schools
Resources
- Harrison T, Shallcross D, Henshaw S (2006) Detecting CO2 – the hunt for greenhouse-gas emissions. Chemistry Review 15: 27-30
- Pacala S, Socolow R (2004) Stabilisation wedges: solving the climate problem for the next 50 years with current technologies. Science 305: 968-972. doi: 10.1126/science.1100103
- Shallcross D (2006) Dirty Air. Education in Chemistry, 43 (5): 131-135
- Veel nota’s van de auteurs bestemd voor leraars over luchtverontreiniging, klimaatsverandering en het ozongat kunnen gevonden op volgende website: www.chemlabs.bristol.ac.uk/outreach/resources/Atmos.html
- Voor een uitstekende bron met grafieken en gegevens betreffende klimaatsverandering, bekijk: www.grida.no/climate/vital/index.htm
- Gegevens van de Earth System Research Laboratory Global Monitoring
- Station kunnen hier gevonden worden: www.cmdl.noaa.gov
- De website van het Intergovernmental Panel on Climate Change, waar het Climate Change 2007 report en andere gegevens te vinden zijn, is: www.ipcc.ch
- Haubold B (2008) An Inconvenient Truth. Science in School 9: 72. www.scienceinschool.org/2008/issue9/inconvenient
Review
De verandering van het klimaat zou zeker een van de onderwerpen moeten zijn van het onderwijs van de hedendaagse wetenschap op alle schoolniveaus overal in Europa. Speciaal na Al Gore’s enorme Inconvenient Truth campagne, heeft dit topic gewonnen aan wereldwijde erkenning. Nochtans zijn nuttige materialen met bruikbare informatie voor de leraars wetenschappen niet altijd onmiddellijk beschikbaar. Dit tweedelig artikel, reikt echter een gepaste en gemakkelijk te veranderen benadering tot het eerder ingewikkeld proces van het modeleren van atmosferische ontwikkelingen.
Waar het wiskundig model het best geschikt is voor gebruik in gevorderde cursussen wetenschap voor leerlingen met een leeftijd van 16 jaar en meer, kunnen de basisfenomenen gemakkelijk aangereikt worden aan leerlingen met een leeftijd van 15 jaar en jonger – zelfs als ze niet de bedoeling hebben later te kiezen voor wetenschappen in de daarop volgende schooljaren. De web bronnen die vermeld worden bieden een ruime keus aan van leerstrategieën en onmiddellijk bruikbare beelden, applets en grafieken, en maken het iedere leraar wetenschappen makkelijker bruikbare bronnen te vinden.
Tobias Kirschbaum, Duitsland





