Supporting materials
Kaip tinklais sklinda epidemija? (Pdf)
Kaip tinklais sklinda epidemija? (Pptx)
Download
Download this article as a PDF

Išvertė Eglė Butkevičiūtė. Supraskite, kaip plinta užkrečiamosios ligos, užsiimdami veikla, pabrėžiančia gyvenimišką mokyklinės matematikos pritaikymą.

Mokyklos – tai tikros infekcijų veisyklos: mokiniai pastoviai susiduria vieni su kitais ir dažnai dar neturi imuniteto ligoms. Svarbu suprasti, kaip tai veikia, kad būtų galima prognozuoti, kaip plis užkrečiamos ligos (tokios, kaip gripas). Moksleiviams svarbu pagalvoti apie savo socialinius ryšius ir suprasti įvairius analizės būdus, naudojamus nustatyti ligų dinamikai.
Šie integruoti užsiėmimai skiriami 12-15 metų amžiaus moksleiviams, nors kai kuriuos galima pritaikyti jaunesniems ar vyresniems mokiniams. Galima tuo užsiimti tiek mažoms grupelėms, tiek visai klasei. Nereikia nieko daugiau nei skaidrių, kurias galima atsisiųsti iš papildomos medžiagos skilties w1, popieriaus ir kauliukų.
Šis trumpas užsiėmimas visai klasei simuliuoja protrūkį ligos, kurios „simptomas“ – reikia atsistoti. Tikslas – suprasti, kaip greitai liga eksponentiškai išplis klasėje. Sulig kiekvienu žingsniu „infekuotų“ mokinių skaičius padvigubės (paveikslėlis nr. 1). Tai padės mokiniams suprasti, kad nereikia daug žingsnių protrūkiui išplisti ligai neatsparioje populiacijoje.
Mokiniai pamatys, kad greitis, kuriuo plinta liga, priklauso nuo ligai neatsparių ar užkrėstų žmonių skaičiaus. Tačiau tai – viso labo paprastas matematinis modelis nustatyti, kaip plinta liga, nes jame daroma prielaida, kad kiekvienas – neatsparus infekcijai ir kad kiekvienas žmogus užkrečia lygiai du kitus.

R0, dar žinomas kaip reprodukcinis skaičius, yra matas, naudojamas epidemiologijoje nurodyti vidutinį skaičių žmonių, kuriuos infekuotas žmogus apkrečia užkrečiamuoju laikotarpiu (darant prielaidą, kad nė vienas populiacijoje nėra atsparus ligai). Jei R0 daugiau nei 1, liga pasklis populiacijoje. Jei R0 mažiau nei 1, ligos atvejų sumažės ir protrūkis baigsis.
R0 kinta priklausomai nuo to, kaip ilgai pacientai gali užkrėsti, ligai neatsparių žmonių skaičiaus populiacijoje ir nuo ligos perdavimo būdo. Oru sklindančios ligos, tokios, kaip tymai, paprastai turi aukštesnį R0 nei per kūno skysčius plintančios, tokios, kaip Ebola.
Epidemiologams svarbu žinoti ne tik skaičių, kiek kitų gali užkrėsti vienas žmogus (R0), bet ir kaip protrūkis gali išplisti populiacijoje. Taigi, svarbu suprasti bendruomenės ar populiacijos dinamiką. Tai daroma stebint, kaip žmonės sąveikauja vieni su kitais: kas kontaktuoja, su kuo ir kiek. Matematiniai modeliuotojai tuomet gali paversti šią informaciją į simuliacijas tam, kad suprastų, kaip protrūkis sklido populiacijoje. Jos būtinos sveikatos mokslų tyrėjams, nes padeda jiems aptikti galimai užsikrėtusius žmones. Taip pat jos gali nurodyti, kokius socialinio elgesio motyvus reikėtų pakeisti prasidėjus protrūkiui, pavyzdžiui, didinant socialinį atstumą ar paskelbiant karantiną.
Nors Ebolos R0 toks žemas kaip ir gripo, jis greitai sukėlė didelį, aukšto mirtingumo (kažko, kas paprastai ribotų ligos plitimą, nes žmonės mirtų per greitai, kad užkrėstų didelę žmonių grupę) protrūkį Vakarų Afrikoje. Tuomet kokios buvo pagrindinės plitimo priežastys?
Epidemija iš dalies kilo atsitiktinai; pirmas užsikrėtęs žmogus buvo liaudies gydytojas iš Siera Leonės, kurio laidotuvės sutraukė didžiulę minią (Freiberger, 2015). Tradicija nuprausti mirusįjį prieš laidojant paskatino užkrato perdavimą ir žmonės, prisilietę prie kūno, išnešiojo ligą keliaudami į kitas vietoves. Taipogi, protrūkis įvyko regione su silpnomis sveikatos apsaugos sistemomis, nepajėgiomis kontroliuoti infekcijos.
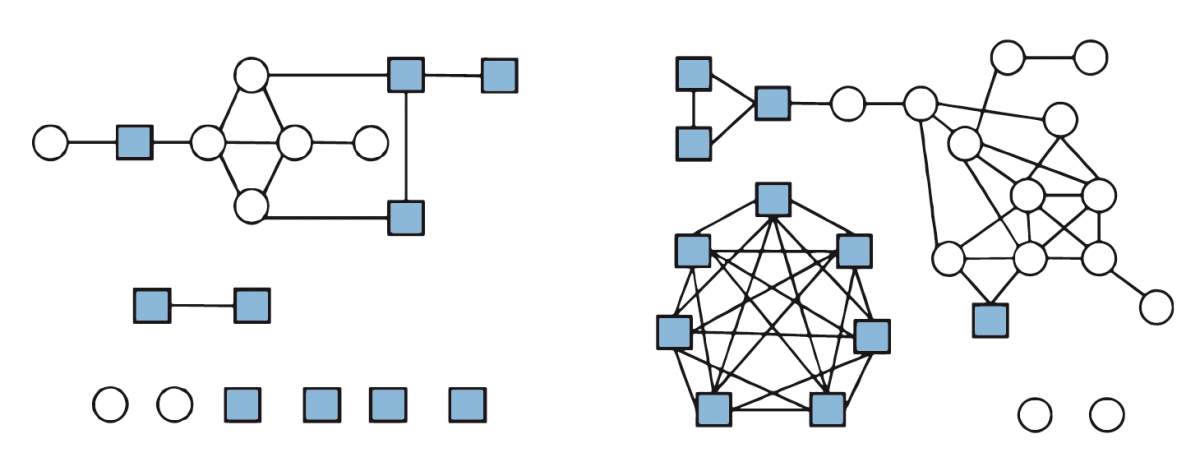
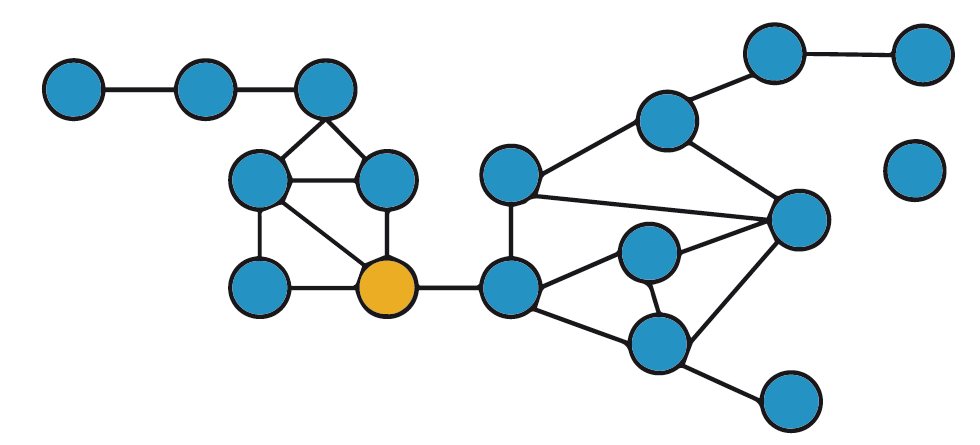
Šis pavyzdys įrodo, kad patogeno R0 gali keistis skirtingų protrūkių metu. Pavyzdžiui, gripo perdavimas skirtųsi keturmečių-penkiamečių ir dešimtmečių-vienuolikamečių grupėse. Paveikslėlis nr. 2 rodo ryšius tarp vaikų šiose dviejose amžiaus grupėse tam tikrą dieną mokykloje. Jaunesniojoje amžiaus grupėje iš viso esama mažiau susidūrimų tarp kelių individų, lyginant su vyresniojo amžiaus grupe, kurioje aiškūs du kiekvienos lyties būriai. Atskiri mazgai be jokios sąveikos rodo, kad mokinio tą dieną nebuvo.
Mokiniai gali apsvarstyti šiuos klausimui individualiai ir aptarti juos su visa klase:
Užsiėmimai pateikti šiame straipsnyje pritaikyti iš „NRICH“ w2 „Ligų dinamikos“ (Disease Dynamics) serijos. Šioje kolekcijoje yra papildomų užsiėmimų, skirtų parodyti, kaip galima pritaikyti matematiką epidemijų, socialinių ryšių ir skiepų veikimo supratimui.
Conlan AJ et al (2011) Measuring social networks in British primary schools through scientific engagement. Proceedings of the Royal Society B: Biological Sciences 278(1771): 1467–1475. doi: 10.1098/rspb.2010.1807
Freiberger M (2015) Ebola in numbers: using mathematics to tackle epidemics. Science in School 32: 14–19.
w1 – Skaidres galite atsisiųsti papildomos medžiagos skiltyje.
w2 – Kad pasižiūrėtumėte į pilną “Ligų dinamikos” seriją, aplankykite „NRICH” puslapį.
Pažaiskite „pandemijos žaidimą“ ir pabandykite išnaikinti pasaulio populiaciją tapę ligas sukeliančiu organizmu.
Simuliuokite lytiniu būdu perduodamų ligų plitimą užsiėmimu klasėje.
Supraskite, kaip gyvūnai gali ligos sukėlėjus perduoti žmonėms:
Heymann J (2013) Evolving threats: investigating new zoonotic infections. Science in School 27: 12–16.
Pasižiūrėkite, kaip archeologijos ir genetikos kombinacija atskleidžia, kas sukėlė Juodąją mirtį:
Bos K (2014) Tales from a plague pit. Science in School 28: 7–11.
Daugiau informacijos faktų rinkinių apie apie infekcines ligas galite rasti Pasaulio sveikatos organizacijos puslapyje.
‘Stop the spread’ – „Practical Action“ STEM (mokslo, technologijos, inžinerijos ir matematikos) iššūkis, kurio tikslas – kad mokiniai galėtų tirti infekcines ligas bei sukurti modelį rankų plovimo įrenginiui mokyklai Kenijoje.
Ligos plitimo populiacijoje modeliavimas reikalauja socialinių kontaktų ir ligos perdavimo modelio išmanymo. Šis straipsnis suteikia mokiniams galimybę suprasti ir skurti modelį ligos bendruomenėje, pavyzdžiui, jų mokykloje arba socialiniame rate. Jis skatins diskusiją apie ligų perdavimą, ligų protrūkių stebėjimą ir kaip veiktų karantinas. Matematikos įtraukimas į šią veiklą mes iššūkį ir skatins mokinius pasitempti, parodant jiems, kad matematika – esminė mokslo ir epidemiologinių tyrimų dalis.
Dr Shelley Goodman, JK