Salviamo la Terra nello stile di Hollywood Teach article
Invitiamo gli studenti a salvare la Terra dalla minaccia di una collisione con un asteroide, utilizzando i calcoli utilizzati dal film di fantascienza Armageddon “Arma letale” di Hollywood.
Gli studenti cosa preferirebbero discutere: i film di Hollywood o la fisica? Durante le mie lezioni di fisica, cerco di combinare questi due argomenti sfruttando gli scenari dei film d fantascienza di Hollywood come una fonte di esercizi indirizzati al problem-solving – in un modo simile all’utilizzazione delle avventure dei personaggi dei personaggi (vedi Follows, 2017). Anche se gli studenti non hanno visti i films, sembra che si divertino sfruttando la loro inventiva nello scenario fantastico, che possono utilizzare come base per fare scienza reale – sempre che le idee e le ipotesi siano posti a loro in modo chiaro.

geralt/pixabay.com
In questo articolo, presento alcuni esercizi che si basano sul film ‘Armageddon’ (1988) – un film di Hollywood su un’eroica missione per salvare la Terra dalla minaccia di un gigantesco asteroide diretto verso la Terra. Il film fu criticato per essere piuttosto irreale, ma comunque offre una interessante sceneggiatura da utilizzare come base per applicare alcuni calcoli.
Armageddon: la storia
Nel film, gli astronomi individuano un asteroide delle dimensioni del Texas con un orbita diretta esattamente verso la Terra avrebbe impiegato esattamente 18 giorni prima dell’impatto. Si stava preparando un piano di far scoppiare una testata nucleare proprio sulla superficie dell’asteroide, con lo scopo di dividere in due che avrebbero dovuto separarsi allontanandosi dalla traiettoria – evitando la Terra. Per mettere in azione questo piano, la NASA aveva imbarcato un estrattore di petrolio Harry Stamper (Bruce Willis) con il suo team, su due navicelle spaziali, che avrebbero compiuto un’orbita di accelerazione attorno alla Luna e ritrovarsi così dietro l’asteroide. Una volta raggiunto l’asteroide, per contrastare il disastro avrebbero dovuto far esplodere la bomba prima che l’asteroide raggiungesse la ‘barriera nulla’, un punto che distava otto ore dopo aver oltrepassato la Luna.
Creazione dell’attività per la classe
Gli studenti avrebbero effettuato una serie di calcoli che si incentravano sulle informazioni fornite dal film, con il complemento di una certa dose di ragionevoli ipotesi. Il divertimento si basa sulla verifica se i dati forniti dal film avevano un certo fondamento scientifico – oppure no.
Dal film, sappiamo che:
- L’asteroide ha le dimensioni del Texas. Assumiamo di riferirci alla sezione principale dell’asteroide approssimativamente sferico.
- L’asteroide si sta dirigendo verso la Terra alla velocità di 22 000 miglia l’ora (35405.54 Km/h).
- Le due sezioni in cui si divide l’asteroide evitano la Terra per circa 400 miglia (640 km).
Le altre informazioni di cui disponiamo sono elencate qui di seguito:
- Il Texas ha un’area di 692 200 km2.
- La densità media dei quattro più grandi asteroidi noti è di 2760 kg m-3. (In confronto, la Terra ha una densità di 5520 kg m-3.)
- La distanza tra la Terra e la Luna è di 384 400 km.
- La Terra ha un raggio di 6400 km.
- L’energia di una testata nucleare è di oltre 50 megatoni di TNT. (Questa è l’energia della più potente arma termonucleare conosciuta: la Testata Sovietica chiamata Big Ivan)
- 1 megatone di TNT è 4.18 x 1015 J
Assumiamo inoltre che:
- L’asteroide sia diretto al Centro della Terra, così che entrambe le due parti in cui si dovrebbe dividere l’asteroide, si dovrebbero allontanare in direzioni opposte e alla stessa distanza.
Domande per gli studenti e calcoli effettuati
Agli studenti è chiesto di verificare se questo piano plausibilmente può salvare la Terra evitando la collisione. Gli studenti si appresteranno ad eseguire una serie di calcoli, come quelli indicati qui di seguito. Gli studenti possono lavorare in gruppi, e sono incoraggiati a discuterne tra loro.
1. Dimostrare che l’asteroide ha un raggio di 470.8 km.
Assumeremo che se la sezione è approssimativamente circolare l’asteroide ha un’area A uguale a quella del Texas, cioè circa 696 200 km2.
A = dove r= raggio dell’asteriode. Così:

2. A che velocità, espressa in unità del sistema metrico decimale (cioè in ms-1) viaggia l’asteroide?
Incoraggiate gli studenti ad eseguire trasformazioni delle unità di misura in maniera formale:

3. A che distanza dalla Terra si trova la ‘barriera zero’?
Per rispondere a questa domanda, per primo abbiamo bisogno di ricavare la distanza che il meteorite percorrerebbe in otto ore, fissiamo la ‘barriera zero’ a questa distanza, cioè quella percorsa dall’asteroide in otto ore, partendo dalla Luna:
Distanza = velocità x tempo
= 9833 m s-1 x 8 x 3600 s
= 2.83 x 108 m
Quindi, sottraendo questo valore alla distanza totale Terra-Luna (3.84 x 108 m) calcoliamo la distanza che l’asteroide dovrebbe ancora viaggiare per entrare in collisione con la Terra.
3.84 x 108 m – 2.83 x 108 m
= 1.01 x 108 m
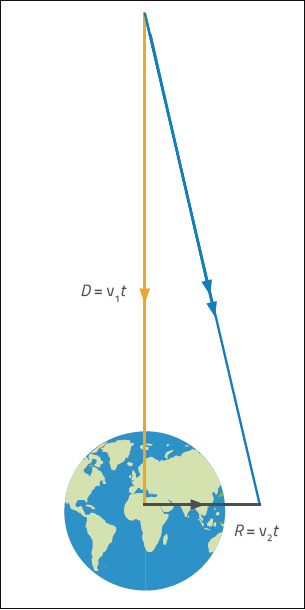
retta gialla mostra la
direzione originale
dell’asteroide. La retta in
nero mostra a quale distanza
ciascuna delle due parti
dovrebbero muoversi al fine
di mancare la Terra di 640
km; la retta in colore blu
mostra il percorso risultante
che le due parti devono
percorrere.
Mike Follow / Graf
4. A che velocità si devono allontanare le due parti in cui si è diviso l’asteroide per evitare l’impatto con la Terra?
Le due metà dell’asteroide dovrebbero allontanarsi di 1.01×108 m dalla ‘barriera zero’ per raggiungere la Terra. Nel tempo necessario a percorrere questa distanza, ogni sezione dell’asteroide dovrà allontanarsi perpendicolarmente alla direzione originale di moto dell’asteroide, ad una distanza sufficiente da non colpire la Terra passando ad almeno 640 km da ogni lato (vedi figura1)
Qui:
D = distanza tra la Terra e la ‘barriera zero’
R = raggio della Terra più i 640 km da cui ogni metà asteroide si deve tenere distante dalla Terra
v1 = velocità alla quale si muove l’asteroide in direzione della Terra.
v2 =Velocità perpendicolare (laterale) di ciascuna parte dell’asteroide affinché non colpisca la Terra con un margine di 640 km
Metodo 1
Per primo, calcoliamo quanto tempo dovrebbe impiegare l’asteroide per raggiungere la barriera zero in prossimità della Terra:
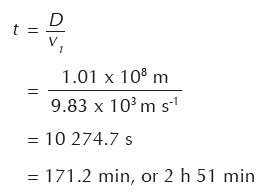
Possiamo calcolarci adesso la velocità alla quale ciascuna parte dell’asteroide dovrebbe muoversi in direzione perpendicolare al percorso originale affinché manchino la Terra con margine di 640 km.
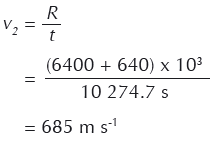
Metodo 2
Per quei studenti che hanno una maggior praticità con la matematica, possiamo impegnarli di conseguenza. Come nel metodo precedente, nel tempo t che l’asteroide impiega a compiere una distanza di 101 000 km in direzione della Terra, i due pezzi devono spostarsi lateralmente per una distanza equivalente al raggio della Terra più 640 km, R. Utilizzando un pò di algebra:

5. Qual’è la massa dell’asteroide (assumendo che abbia una densità tipica di un asteroide)?
La massa m è uguale a densità r moltiplicato il volume V, così m = ρ x V
L’asteroide è approsimativammente sferico, così V = 4 ⁄ 3 π R3
Dalla domanda 1, R = 470.8 km
Così M = ρπR3
= 2760 kg m-3 x 4/3 π x (4.71 x 105 m)3
= 1.21 x 1021 kg
6. Quanta energia cinetica dobbiamo fornire alle due semisfere dell’asteroide affinché si eviti la collisione con la Terra?
Nota: si deve ottenere la stessa risposta se si tratta l’asteroide intero o costituito dalle due semisfere separate.
E = 1/2 mv2
= 1/2 x 1.2 x 1021 kg x (685 m s-1)2
= 2.84 x 1026 J
7. Quante testate nucleari delle stesse dimensioni di Big Ivan sono necessarie per ottenere questa energia?
Una testata Big Ivan è equivalente a 50 megatoni di TNT= 50 x 4.18 x 1015 J
= 2.09 x 1017 J
Così l’energia necessaria per far cambiare la traiettoria all’asteroide e mancare la collisione con la Terra è equivalente a:
![]()
8. A che velocità si separeranno le due semisfere dell’asteroide se si usasse una sola testata del tipo del Big Ivan?
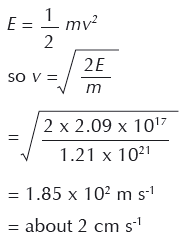
9. Di quanto si allontanano le due calotte quando collideranno con la Terra, se venisse usata solo una testata del tipo Big Ivan?
Abbiamo già dimostrato (nella domanda 4) che l’asteroide dalla barriera zero si trova a meno di tre ore dall’impatto. Alla velocità di 1.85 x 102 m s-1 in quel tempo ciascuna delle due semiparti dell’asteroide si allontaneranno di 190 m dal percorso principale, così le due metà si muoveranno allontanandosi l’una dall’altra di meno 400 m – troppo poco per evitare la collisione con la Terra. Infatti, nelle condizioni descritte nel film, la squadra avrebbe bisogno di intercettare l’asteroide quando si trova a circa 3.74 x 1012 km – 25 volte la distanza Terra Sole, e nello spazio la distanza tra Urano e Nettuno.
A volte si dimostra che si ha bisogno di qualcosa anche più grande di una esplosione nucleare affinché si eviti la collisione.

Jack W. Aeby (dominio pubblico)/Wikimedia Commons
Discussione
Vi sono molte cose di cui discutere con gli studenti, dopo aver fatto o assieme ai calcoli. Gli studenti potranno avere le loro opinioni per rendere gli scenari più realistici – o su quali eventi o assunzioni sono i più assurdi. Per esempio, perché gli scienziati fallirebbero di centrare l’asteroide a meno che non sia più vicino? E nonostante questo fallimento, come hanno fatto a capire che aveva attraversato una faglia, esattamente lungo la direzione della traiettoria?
Qui di seguito alcuni suggerimento e altri punti da considerare:
- I calcoli non includono l’energia richiesta per romper il legame chimico per dividere l’asteroide nelle due parti: includono solo l’energia richiesta a separare le due metà, assumendo che l’asteroide fosse già convenientemente fratturato. Se sommiamo l’energia per fratturare l’asteroide, di quanto variano i calcoli?
- Se l’asteroide dovesse colpire la Terra, quale dovrebbe essere l’energia dell’urto? Gli studenti possono ricavarla dall’energia cinetica dell’asteroide. Troveranno che l’urto con la Terra dovrebbe rilasciare 5.8 x 1028 J – equivalente a 276 miliardi (2.76 x 1011) Big Ivan. In confronto, l’asteroide che ha provocato la distruzione del Cretaceo (e l’estinzione dei dinosauri) 65 milioni di anni fa aveva rilasciato solamente 4 x 1023 (2 milioni di Big Ivan).
- Gli studenti possono osservare gli oggetti della vita reale che potrebbero dirigersi sulla Terra, e ricavare quanto quello di Armaggeddon è simile a questi asteroidi. Alla velocità di 9833 m s-1, la sua velocità è più lento della media degli asteroidi, che hanno una velocità di circa 25 000 m s-1. (In confronto, la cometa di Halley ha una velocità di 53 600 m s-1 quando viene a trovarsi più vicino al Sole, al suo perielio). Il programma di ricerca della NASA il NEOw1 (oggetti in prossimità della Terra) serve a tracciare la traiettoria di quegli oggetti che potrebbero scontrarsi con la Terra: uno di questi è l’asteroide (29075) 1950 DA, che ha un diametro di circa 1 km. C’é la probabilità di 1 su 300 di scontrarsi con la Terra nel 2880.

References
- Follows M (2017) Heroes and villains: the science of superheroes. Science in School 40: 57-63.
Web References
- w1 – Le leggere le ultime notizie dal Centro per lo Studio degli Oggetti di Prossimità alla Terra (Near Earth Objects Studies) visitate il sito web della NASA.
Resources
- Si può leggere della buona e della cattiva scienza riportata in Armageddon visitando il sito web Bad Astronomy.
- Per informazioni sugli asteroidi e comete, visitate il sito web molto accurato di Bill Arnett Nine Planets.
- Potete ascoltare TED che spiega come potreste difendere la Terra dagli asteroidi nel sito web TED.
- Il Centro di Sorveglianza The Spaceguard Centre (nel Regno Unito a Knighton Powys) fornisce informazioni sulla minaccia rappresentata dall’impatto dagli asteroidi e delle comete, e i modi per predire e trattare queste minacce, visitate il loro sito web.
- Le immagini del sito web del Sistema Solare offre un catalogo dei crateri d’impatto sulla Terra.
- Per critiche ulteriori ed esplorazioni sulle scienze nei film, si possono consultare i seguenti libri:
- Rogers T (2007) Insultingly Stupid Movie Physics. Naperville, IL, USA: Sourcebooks Hysteria. ISBN: 1402210337
- Perkowitz S (2010) Hollywood Science: Movies, Science, and the End of the World. New York, USA: Columbia University Press. ISBN: 0231142811
- Weiner A (2007) Don’t Try This at Home! The Physics of Hollywood Movies. New York, USA: Kaplan Publishing. ISBN: 1419594060
- Edwards R, Brooks M (2017) Science(ish): The Peculiar Science Behind the Movies. London, UK: Atlantic Books. ISBN: 1786492210
Review
Questa attività è molto interessante e divertente per gli studenti. Cosa c’é di meglio che stimolare la curiosità degli studenti e porli di fronte ai problemi in modo creativo? Verificare e smontare i fatti ricavati dai film permette gli studenti di formalizzare le proprie domande su questi fatti, e come si può rispondere applicando le loro conoscenze in fisica e matematica. Non importa quanto possano essere irreali questi scenari dei film, vi sarà sempre un principio fisico che li può aiutare a spiegare se sono possibili o impossibili.
L’utilizzo delle scienze per spiegare i film di fantascienza possono portare anche ad elaborate discussioni quando gli studenti ripensano ai fatti presentati nei film e non li prendano per veri. Gli studenti possono essere motivati ad espandere la loro area di ricerca se necessario, e dimostrare i loro argomenti con prove matematiche. Questo esercizio può anche porre gli studenti a considerare che i fatti scientifici si trovano dovunque, sia nella vita reale che nella finzione.
Catherine Cutajar, lettrice di fisica, presso il Collegio St Martin di Malta





