Historias gráficas Teach article
Esta actividad se presentó en el Festival Science on Stage 2022 ![]()
Dibuja gráficos a partir de vídeos de sucesos cotidianos para ayudar a los alumnos a comprender las características básicas de los gráficos y cómo interpretarlos.

La idea de dibujar un gráfico a partir de historias es sencilla. Se muestra a los alumnos una breve película de un acontecimiento cotidiano, como un vaso que se llena de agua, un trozo de salmón que se cocina en el horno o una bicicleta que baja una colina. A continuación, se les pide que dibujen un gráfico que describa el suceso, por ejemplo, cómo creen que cambia la altura del agua, la temperatura del salmón o la velocidad de la bicicleta a lo largo del tiempo. Estos bocetos se convierten en el punto de partida de un debate en el aula, que finaliza con la visualización del gráfico correcto.
A continuación se muestra un ejemplo de un vídeo de historias gráficas.
Para dibujar el gráfico que describe el aumento de la temperatura del salmón en el horno, los alumnos tendrán que pensar en los puntos inicial y final del gráfico y en la forma que adoptará el gráfico entre esos puntos. ¿Será una línea recta o una curva? Este enfoque se centra, pues, en las características globales de la gráfica. De este modo, la actividad complementa las lecciones en las que los alumnos construyen gráficos punto por punto, por ejemplo, las lecciones en las que los alumnos realizan sus propios experimentos, recogen datos y los visualizan gráficamente.
Esta rutina de hacer historias con gráficos fue promovida por el educador matemático estadounidense Dan Meyer. Es adecuada para estudiantes de entre 13 y 19 años, y hacer un gráfico de una sola historia suele llevar entre 10 y 20 minutos.
Cómo utilizar los vídeos de historias gráficas
Materiales
- Los alumnos necesitarán lápices y papel cuadriculado.
- Se puede acceder a los vídeos de la historia aquí.
Procedimiento
- Muestre a los alumnos la primera parte de la película. Ponga en pausa la película después de que se muestre el sistema de coordenadas y se vean las variables relevantes en los ejes. Explique que los alumnos deben dibujar un gráfico del evento, describiendo la relación entre las dos variables.
- Explique a los alumnos que no tienen toda la información necesaria para dibujar el gráfico, por lo que tendrán que hacer algunas suposiciones y estimaciones. En la historia gráfica anterior, por ejemplo, los alumnos tienen que estimar el tiempo que se tardó en cocinar el salmón.
- De tiempo a los alumnos para que dibujen un sistema de coordenadas en sus cuadernos. Dependiendo de los conocimientos previos, puede ser necesario aclarar qué variables deben trazarse en cada eje y qué escalas podrían tener los ejes. También puede optar por repartir papel cuadriculado ya preparado. Si los alumnos no necesitan ayuda, es un buen ejercicio para que dibujen su propio sistema de coordenadas y elijan una escala adecuada.
- Reinicie la película para mostrar el evento una vez más. Dependiendo de la naturaleza de la historia gráfica, puede ser necesario reproducir la película varias veces o reproducirla a una velocidad más lenta. Si los alumnos tienen sus propios ordenadores, puede optar por darles acceso a la película, para que puedan verla varias veces y también detenerla si es necesario.
- Dé a los alumnos tiempo para dibujar el gráfico. Pasee por el aula y observe el trabajo de los alumnos. A aquellos alumnos que tengan dificultades para empezar se les puede aconsejar que primero describan con palabras la relación entre las variables, por ejemplo: “Creo que la temperatura del salmón aumenta a un ritmo constante”. Una vez formulada la hipótesis con palabras, suele ser más fácil trasladar esta idea a un gráfico. Puede ser útil que los alumnos trabajen en parejas.
Estas tres preguntas también son una buena forma de apoyar a los alumnos:- ¿En qué punto debe comenzar el gráfico?
- ¿En qué punto debería terminar el gráfico?
- ¿Qué aspecto crees que tiene el gráfico en el punto intermedio?
- Seleccione algunas gráficas que muestren ideas matemáticas diferentes para compararlas en un debate con toda la clase. Por ejemplo, puede seleccionar gráficos que tengan formas diferentes, la misma forma pero diferentes puntos de inicio y final, o diferentes escalas en los ejes. Busque gráficos que manifiesten conceptos erróneos comunes
- Presente los gráficos seleccionados a la clase. Los alumnos pueden describir sus gráficos oralmente, mientras usted los dibuja en la pizarra, o los alumnos pueden salir a la pizarra y dibujar sus gráficos. Una cámara y un proyector o un sistema de presentación digital son otras posibilidades.
- Guíe el debate en clase para ayudar a los alumnos a comprender las características clave de sus gráficos sugeridos y cómo se relacionan con el acontecimiento mostrado en el vídeo. Ver el apartado Discusión más adelante.
- De tiempo a los alumnos para que revisen sus gráficos basándose en lo que han aprendido durante la discusión. Al hacer hincapié en que el primer gráfico es un borrador, resulta menos arriesgado que los alumnos se equivoquen. Esto, a su vez, puede aumentar la participación en la discusión en clase.
- Reinicie el vídeo y muestre el gráfico correcto. Discuta las similitudes y diferencias entre el gráfico correcto y las sugerencias de los alumnos. Esto puede llevar a los alumnos a conclusiones como
“Pensábamos que el salmón tardaba 20 minutos en cocinarse, ¡pero tardó mucho más que eso!”
“Parece que la temperatura del salmón aumentó más rápido hacia la mitad del tiempo de cocción. No me lo imaginaba”.
“Pensé que la temperatura del salmón aumentaba linealmente, pero no fue así”.
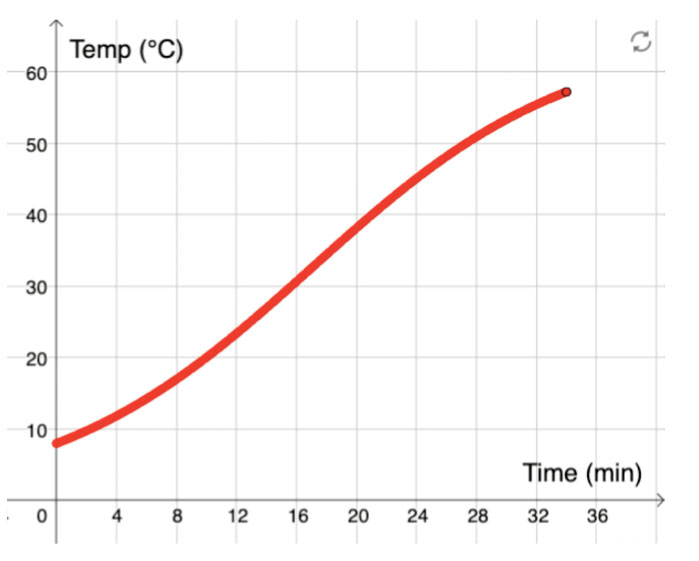
Imagen cortesía de Emelie Reuterswärd
Discusión
Una buena manera de guiar el debate en clase, tras la primera ronda de esbozos de gráficos, es comparar dos gráficos y animar a los alumnos a describir sus similitudes y diferencias.
Por ejemplo, los gráficos siguientes muestran dos posibles descripciones de cómo aumenta la temperatura del salmón mientras se cocina en el horno.
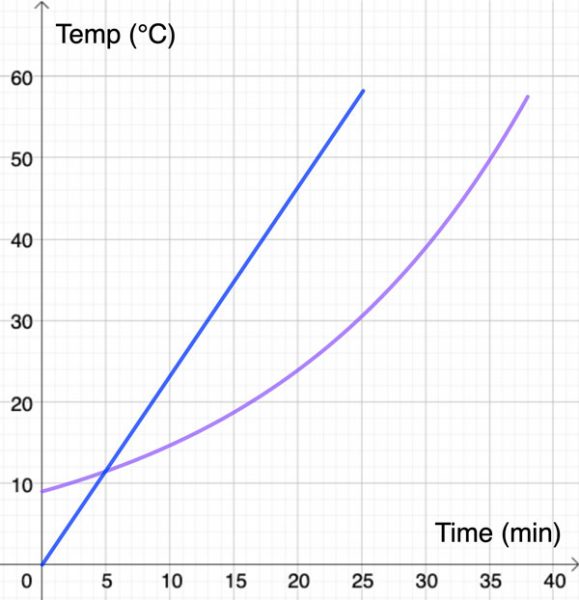
Cuando los estudiantes comparen estos dos gráficos, podrían darse cuenta que:
- la gráfica azul comienza en el origen, mientras que la gráfica púrpura tiene una intersección en el eje y más alta;
- el alumno que ha dibujado la gráfica púrpura piensa que el salmón tarda más en cocinarse;
- la gráfica azul muestra que la temperatura del salmón aumenta a un ritmo constante, mientras que la morada muestra que la temperatura del salmón aumenta más rápidamente al final.
Al reformular las afirmaciones de los alumnos utilizando vocabulario matemático, puede introducir conceptos matemáticos importantes, como “lineal”, “pendiente” y “dominio”.
Otra forma de profundizar en el debate en clase es centrarse en diferentes partes de la gráfica y dejar que los alumnos expliquen su pensamiento: ¿Por qué la gráfica no empieza en el origen? ¿Por qué se ha elegido esa escala? ¿Por qué la gráfica es más empinada al final?
Ideas para ampliar la tarea
Una vez completada la historia, hay varias formas de ampliar la tarea. Se puede pedir a los alumnos que determinen la ecuación que describe la gráfica o que determinen el dominio y el rango de la función. También se puede ampliar la tarea preguntando “¿Qué pasa si?” Para el ejemplo del salmón, estas preguntas podrían ser
- ¿Cómo sería el gráfico si cocináramos un trozo de salmón más pequeño? ¿O uno más grande?
- ¿Cómo sería la gráfica si pusiéramos un trozo de salmón congelado?
- ¿Cómo sería la gráfica si dejáramos el salmón más tiempo en el horno?
Animar a los alumnos a plantear este tipo de preguntas les capacita para explorar las características y limitaciones de un modelo matemático y les enseña a pensar como un matemático.
También es eficaz trabajar con varias historias gráficas seguidas. De este modo, pueden comparar y contrastar diferentes gráficos y establecer conexiones entre distintos conceptos matemáticos. Por ejemplo, la historia ‘la velocidad de la bicicleta’ pide a los alumnos que hagan una gráfica de la velocidad de una bicicleta en función del tiempo, conforme la bicicleta baja una colina, reduce la velocidad y finalmente se detiene. La gráfica resulta ser una parábola casi perfecta. Pero ¿qué pasa con la gráfica que describe la distancia recorrida en función del tiempo? Esta pregunta se responde en la historia gráfica ‘distancia en bicicleta’. Al dejar que los alumnos trabajen con estas dos historias gráficas, pueden establecer conexiones entre conceptos como las funciones derivada y primitiva.
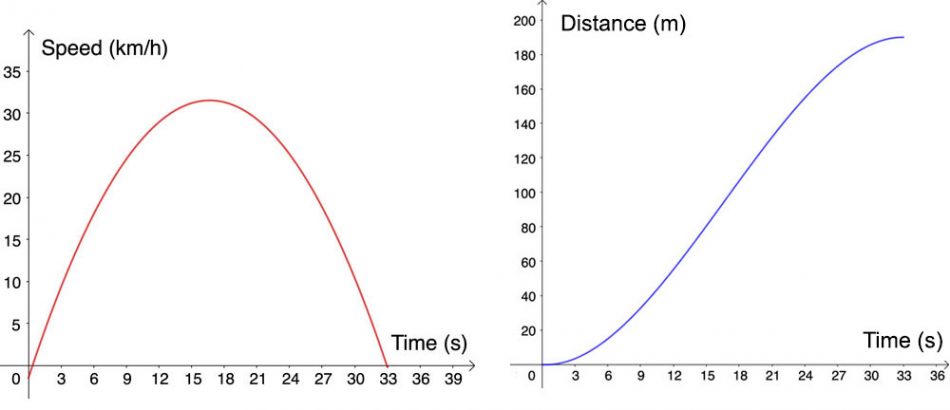
Imagen cortesía de Emelie Reuterswärd
Como extensión, puede dejar que sus alumnos creen sus propias historias gráficas utilizando sus teléfonos móviles. Esto les anima a ver las matemáticas en los acontecimientos cotidianos y a describirlos con un modelo matemático. En secundaria, las películas pueden explorar fenómenos de otras asignaturas, como la física o la formación profesional. De este modo, las películas de los alumnos pueden convertirse en el punto de partida de una actividad de aprendizaje interdisciplinar.
¿Por qué utilizar historias gráficas?
¿Por qué utilizar historias gráficas?
- Los alumnos experimentan cómo se utilizan los gráficos para describir fenómenos cotidianos. Conecta las matemáticas con la realidad de los alumnos y les permite ver la utilidad de las matemáticas.
- La discusión en clase de las gráficas de los alumnos plantea la necesidad de formular lo que los alumnos han dibujado. Esto brinda la oportunidad de introducir conceptos importantes, como pendiente, lineal, constante, creciente y decreciente. En el segundo ciclo de secundaria, se pueden utilizar las historias gráficas para discutir conceptos más avanzados, como las derivadas, el punto de inflexión y el máximo.
- Después de trabajar con varias historias gráficas diferentes, un paso natural es comparar las gráficas y clasificarlas. Así, las historias gráficas son una excelente herramienta para introducir y hablar de relaciones, por ejemplo, lineales, cuadráticas, periódicas y exponenciales.
- En el primer ciclo de secundaria, es habitual trabajar principalmente con relaciones lineales. Con la ayuda de las historias gráficas, se puede mostrar a los alumnos que existen otros tipos de relaciones, cuyas gráficas no son líneas rectas.
- La elaboración de gráficos de acontecimientos cotidianos es una tarea habitual en muchos libros de texto. Dejar que los alumnos vean una película del suceso lo hace más concreto, lo que puede facilitar a los alumnos el dibujo del gráfico. Además, la conexión entre el suceso y el gráfico se hace más fuerte.
- Dibujar gráficos de sucesos cotidianos es una tarea difícil que a menudo puede descubrir conceptos erróneos ocultos. Por ejemplo, los alumnos suelen tener dificultades para encontrar una escala adecuada y no consiguen espaciar las cantidades de forma equitativa a lo largo del eje. El hecho de tener que razonar las cosas en lugar de limitarse a trazar los datos puede revelar a menudo conceptos erróneos ocultos.
Este último aspecto es un punto fuerte de este enfoque. Un error común son las llamadas representaciones “icónicas” de los gráficos. Esto significa que el alumno ve una correspondencia entre la forma del gráfico y una característica visual del evento descrito. Por ejemplo, los alumnos que trabajan con la historia gráfica “velocidad de la bicicleta” pueden dibujar una gráfica que se asemeja a la forma del valle por el que pasó la bicicleta (gráfica de la izquierda), en lugar de una parábola con un punto máximo (gráfica de la derecha).
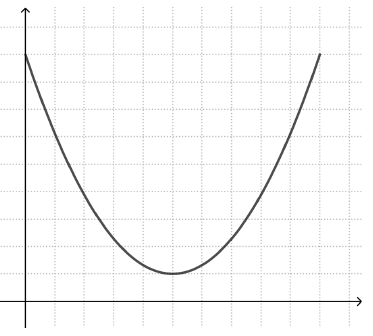
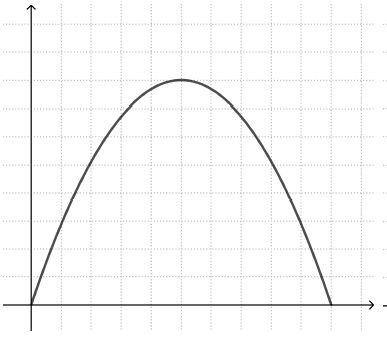
Del mismo modo, un estudiante que intenta dibujar un gráfico de cómo cambia la altura de un columpio en movimiento con el tiempo puede dibujar un gráfico que se asemeja al movimiento del columpio hacia adelante y hacia atrás (gráfico de la izquierda), en lugar de un gráfico periódico que alterna entre los valores altos y bajos de y (gráfico de la derecha).

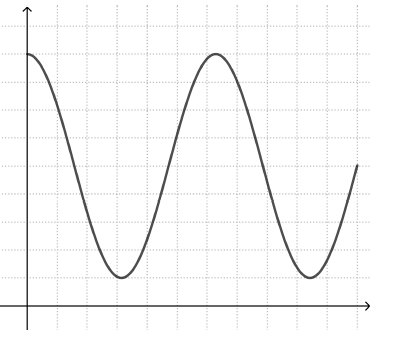
El enfoque gráfico de la historia hace visibles estos conceptos erróneos y ofrece excelentes oportunidades para que los estudiantes los discutan y los superen.
Resources
- Lea más sobre las historias gráficas y acceda a los vídeos de historias gráficas en www.matemagi.com/graphingstories
- Explique a sus alumnos el crecimiento exponencial mediante estos sencillos ejercicios: : Vieser W (2021) Exponential growth 1: learn the basics from confetti to understand pandemics. Science in School 53.
- Observe el crecimiento exponencial a través de la invención del ajedrez y la propagación de enfermedades infecciosas: Vieser W (2021) Exponential growth 2: real-life lessons from the COVID-19 pandemic. Science in School 53.
- Lea sobre la importancia de las estadísticas y el correcto análisis de los datos: Le Guillou I (2021) Clinical trials count on more than statistics. Science in School 52.
- Involucre a sus alumnos y demuestre la física fundamental con objetos cotidianos: de Winter J (2022) Physics with everyday objects: springy sweets, a universe in your pocket, and drawing circuits. Science in School 56.
Institutions
Science on StageReview
Este artículo trata sobre las historias con gráficos. Se muestra a los alumnos un corto de un hecho cotidiano, como un vaso que se llena de agua, y se les pide que dibujen un gráfico de dicha cuestión. Estos dibujos se discuten en clase. Este enfoque debería ayudarles a comprender mejor los conceptos de un gráfico. Curiosamente, en las películas no se habla ni se muestra ningún texto. Esto hace que este enfoque sea especialmente adecuado para los alumnos con dificultades lingüísticas. Si el profesor presta atención al vocabulario (matemático) al hablar de los gráficos, los alumnos pueden mejorar también sus habilidades lingüísticas.
Annemiek van Leendert, Math teacher, Royal Visio, the Netherlands





