Κάνοντας γραφικές παραστάσεις ιστοριών Teach article
Αυτή η δραστηριότητα παρουσιάστηκε στο Φεστιβάλ Science on Stage 2022 ![]()
Σχεδιάστε γραφικές παραστάσεις απο «ιστορίες» βίντεο καθημερινών γεγονότων, για να βοηθήσετε τους μαθητές να κατανοήσουν τα βασικά χαρακτηριστικά των γραφικών…

Η ιδέα της δημιουργίας γραφικών παραστάσεων από ιστορίες είναι απλή. Οι μαθητές παρακολουθούν μία ταινία μικρής χρονικής διάρκειας από ένα καθημερινό γεγονός, όπως ένα ποτήρι γεμάτο με νερό, ένα κομμάτι σολομού που μαγειρεύεται στο φούρνο ή ένα ποδήλατο που κατεβαίνει ένα λόφο. Στη συνέχεια ζητείται από τους μαθητές να σχεδιάσουν μία γραφική παράσταση που να περιγράφει το γεγονός, π.χ. πώς νομίζουν ότι αλλάζει το ύψος του νερού, η θερμοκρασία του σολωμού ή η ταχύτητα του ποδηλάτου με την πάροδο του χρόνου. Αυτά τα σκίτσα γίνονται το σημείο εκκίνησης για να ξεκινήσει μια συζήτηση στην τάξη, η οποία τελειώνει με την εμφάνιση της σωστής γραφικής παράστασης.
Ακολουθεί ένα παράδειγμα δημιουργίας γραφικής παράστασης από βιντεοϊστορία.
Για να σχεδιάσουν τη γραφική παράσταση η οποία περιγράφει την αύξηση της θερμοκρασίας του σολομού στον φούρνο, οι μαθητές θα πρέπει να σκεφτούν τα σημεία αρχής και τέλους της γραφικής παράστασης, και το σχήμα του γραφήματος μεταξύ αυτών των δύο σημείων. Θα είναι μια ευθεία γραμμή ή μία καμπύλη; Συνεπώς, αυτή η προσέγγιση εστιάζει στα καθολικά χαρακτηριστικά της γραφικής παράστασης. Με αυτόν τον τρόπο, η δραστηριότητα συμπληρώνει μαθήματα στα οποία οι μαθητές κατασκευάζουν γραφικές παραστάσεις σημείο προς σημείο, για παράδειγμα, μαθήματα όπου οι μαθητές διεξάγουν τα δικά τους πειράματα, συλλέγουν δεδομένα, και οπτικοποιούν τα δεδομένα γραφικά.
Αυτή η διαδικασία σχεδιασμού ιστοριών πρωτοξεκίνησε από τον Αμερικανό εκπαιδευτικό μαθηματικών Dan Meyer. Είναι κατάλληλη για μαθητές ηλικίας 13-19 ετών και η γραφική παράσταση μιας ιστορίας, συνήθως, διαρκεί περίπου 10-20 λεπτά.
Πως να χρησιμοποιήσετε τα βίντεο με ιστορίες που μπορούν να παρασταθούν γραφικά
Υλικά
- Οι μαθητές θα χρειαστούν μολύβια και τετραγωνισμένο χαρτί
- Τα story video μπορείτε να τα δείτε εδώ.
Διαδικασία
- Δείξτε το πρώτο μέρος της ταινίας στους μαθητές. Σταματήστε την ταινία μετά την εμφάνιση του συστήματος συντεταγμένων και των σχετικών μεταβλητών που είναι ορατές στους άξονες. Εξηγήστε ότι οι μαθητές πρέπει να σχεδιάσουν μία γραφική παράσταση του γεγονότος, περιγράφοντας τη σχέση μεταξύ των δύο μεταβλητών.
- Εξηγήστε στους μαθητές ότι δεν έχουν όλες τις πληροφορίες που χρειάζονται για να σχεδιάσουν τη γραφική παράσταση, επομένως θα πρέπει να κάνουν κάποιες υποθέσεις και εκτιμήσεις. Στην παραπάνω γραφική παράσταση, για παράδειγμα, οι μαθητές πρέπει να εκτιμήσουν πόσος χρόνος χρειάστηκε για να μαγειρέψουν τον σολομό.
- Δώστε χρόνο στους μαθητές να σχεδιάσουν ένα σύστημα συντεταγμένων στα τετράδιά τους. Ανάλογα με τις προηγούμενες γνώσεις, μπορεί να είναι απαραίτητο να διευκρινιστεί ποιες μεταβλητές πρόκειται να παρασταθούν σε κάθε άξονα και ποια κλίμακα θα μπορούσαν να έχουν οι άξονες. Μπορείτε επίσης να επιλέξετε να μοιράσετε έτοιμο χαρτί γραφικών παραστάσεων. Εάν οι μαθητές δεν χρειάζονται υποστήριξη, είναι μια καλή άσκηση για αυτούς να σχεδιάσουν το δικό τους σύστημα συντεταγμένων και να διαλέξουν μια κατάλληλη κλίμακα.
- Επανεκκινήστε την ταινία για να δείξετε άλλη μια φορά το γεγονός. Ανάλογα με τη φύση της ιστορίας με γραφική πaράσταση, μπορεί να χρειαστεί να προβάλετε την ταινία πολλές φορές ή να την προβάλετε με μικρότερη ταχύτητα. Εάν οι μαθητές έχουν τους δικούς τους υπολογιστές, μπορείτε να επιλέξετε να τους δώσετε πρόσβαση στην ταινία, έτσι ώστε να μπορούν να την παρακολουθήσουν αρκετές φορές και να τη σταματήσουν αν χρειαστεί.
- Δώστε χρόνο στους μαθητές να σχεδιάσουν τη γραφική παράσταση. Περπατήστε στην τάξη και παρατηρήστε τη δουλειά των μαθητών. Συμβουλεύστε τους μαθητές που δυσκολεύονται να ξεκινήσουν, να περιγράψουν πρώτα τη σχέση μεταξύ των μεταβλητών με λέξεις, π.χ., «Νομίζω ότι η θερμοκρασία του σολομού αυξάνεται με σταθερό ρυθμό». Μόλις μια υπόθεση διατυπωθεί με λόγια, είναι συχνά ευκολότερο να μεταφερθεί αυτή η ιδέα σε μία γραφική παράσταση. Μπορεί να είναι χρήσιμο οι μαθητές να εργάζονται σε ζευγάρια.
Αυτές οι τρεις ερωτήσεις είναι επίσης ένας καλός τρόπος να υποστηρίξετε τους μαθητές:- Από ποιο σημείο πρέπει να ξεκινά η γραφική παράσταση;
- Σε ποιο σημείο πρέπει να τελειώνει η γραφική παράσταση;
- Πώς πιστεύετε ότι μοιάζει η γραφική παράσταση μεταξύ των δύο σημείων;
- Επιλέξτε μερικές γραφικές παραστάσεις που παρουσιάζουν διαφορετικές μαθηματικές ιδέες για σύγκριση, σε μια συζήτηση στην ολομέλεια της τάξης. Για παράδειγμα, μπορείτε να επιλέξετε γραφικές παραστάσεις που έχουν διαφορετικά σχήματα, το ίδιο σχήμα αλλά διαφορετικά σημεία αρχής και τέλους ή διαφορετικές κλίμακες στους άξονες. Αναζητήστε γραφικές παραστάσεις που εμφανίζουν κοινές παρανοήσεις.
- Παρουσιάστε τις επιλεγμένες γραφικές παραστάσεις στην τάξη. Οι μαθητές μπορούν να περιγράψουν τις γραφικές τους παραστάσεις προφορικά, καθώς εσείς τις σχεδιάζετε στον πίνακα, ή οι μαθητές μπορούν να έρθουν και να σχεδιάσουν οι ίδιοι τις γραφικές τους παραστάσεις στον πίνακα. Μια κάμερα και ένας προτζέκτορας ή ένα ψηφιακό σύστημα προβολής είναι κάποιες άλλες δυνατότητες.
- Καθοδηγήστε τη συζήτηση στην τάξη ώστε να βοηθήσετε τους μαθητές να κατανοήσουν τα βασικά χαρακτηριστικά των προτεινόμενων γραφικών παραστάσεων και πώς αυτά σχετίζονται με το γεγονός που εμφανίζεται στο βίντεο. Βλέπε Συζήτηση.
- Δώστε χρόνο στους μαθητές να διορθώσουν τις γραφικές τους παραστάσεις με βάση αυτά που έμαθαν κατά τη διάρκεια της συζήτησης. Τονίζοντας ότι η πρώτη γραφική παράσταση είναι προσχέδιο, γίνεται λιγότερο επικίνδυνο για τους μαθητές να κάνουν λάθος. Αυτό, με τη σειρά του, μπορεί να αυξήσει τη συμμετοχή στη συζήτηση στην τάξη.
- Προβάλετε ξανά το βίντεο και δείξτε τη σωστή γραφική παράσταση. Συζητήστε τυχόν ομοιότητες και διαφορές μεταξύ της σωστής γραφικής παράστασης και των προτάσεων των μαθητών. Αυτό μπορεί να οδηγήσει τους μαθητές σε συμπεράσματα όπως π.χ
«Νομίσαμε ότι χρειάστηκαν 20 λεπτά για να μαγειρευτεί ο σολομός, αλλά διήρκεσε περισσότερο από αυτό!»
«Φαίνεται ότι η θερμοκρασία του σολομού αυξήθηκε περισσότερο στα μέσα του χρόνου μαγειρέματος. Δεν το πίστευα!»
«Νόμιζα ότι η θερμοκρασία του σολομού αυξήθηκε γραμμικά, αλλά δεν έγινε έτσι.»
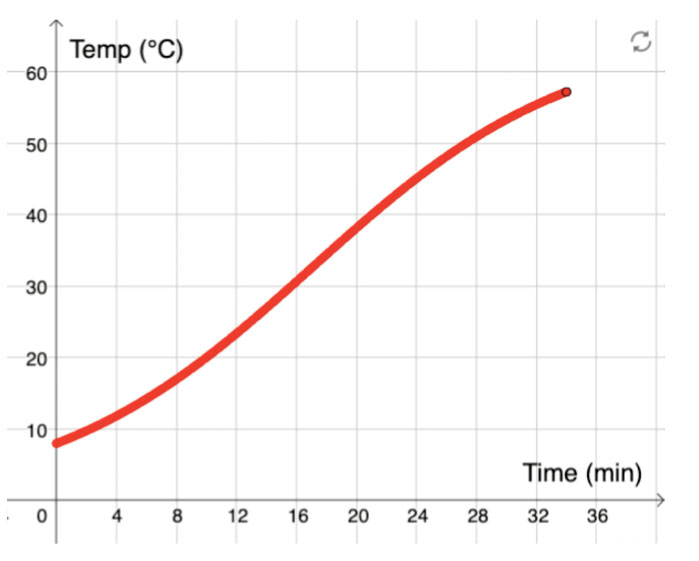
Η εικόνα είναι ευγενική προσφορά της Emelie Reuterswärd
Συζήτηση
Ένας καλός τρόπος για να καθοδηγήσετε τη συζήτηση στην τάξη μετά τον πρώτο γύρο σχεδιασμού των γραφικών παραστάσεων είναι να συγκρίνετε δύο γραφικές παραστάσεις και να ενθαρρύνετε τους μαθητές να περιγράψουν τις ομοιότητες και τις διαφορές τους.
Για παράδειγμα, οι παρακάτω γραφικές παραστάσεις δείχνουν δύο πιθανές περιγραφές για το πώς αυξάνεται η θερμοκρασία του σολομού καθώς ψήνεται στο φούρνο.
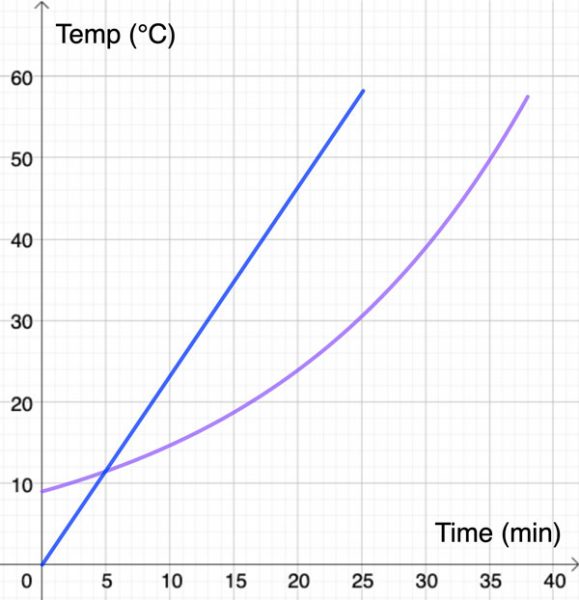
Όταν οι μαθητές συγκρίνουν αυτές τις γραφικές παραστάσεις, μπορεί να παρατηρήσουν ότι:
- η μπλε γραφική παράσταση ξεκινά από την αρχή, ενώ η μωβ γραφική παράσταση έχει υψηλότερο σημείο τομής με τον άξονα y.
- ο μαθητής που έχει σχεδιάσει τη μωβ γραφική παράσταση πιστεύει ότι χρειάζεται περισσότερος χρόνος για να ψηθεί ο σολομός.
- Η μπλε γραφική παράσταση δείχνει ότι η θερμοκρασία του σολομού αυξάνεται με σταθερό ρυθμό, ενώ η μωβ δείχνει ότι η θερμοκρασία του σολομού αυξάνεται πιο γρήγορα στο τέλος.
Αναδιατυπώνοντας τις δηλώσεις των μαθητών χρησιμοποιώντας μαθηματική ορολογία, μπορείτε να εισάγετε σημαντικές μαθηματικές έννοιες, όπως «γραμμικός», «κλίση» και «πεδίο ορισμού».
Ένας άλλος τρόπος για να προχωρήσετε περαιτέρω τη συζήτηση στην τάξη είναι να εστιάσετε σε διαφορετικά τμήματα της γραφικής παράστασης, και να αφήσετε τους μαθητές να εξηγήσουν τη σκέψη τους: Γιατί η γραφική παράσταση δεν ξεκινά από την αρχή; Γιατί επιλέξατε αυτή την κλίμακα; Γιατί η γραφική παράσταση είναι πιο απότομη στο τέλος;
Ιδέες για επέκταση της εργασίας
Αφού ολοκληρώσετε μια ιστορία, υπάρχουν αρκετοί τρόποι για να επεκτείνετε την εργασία. Μπορείτε να ζητήσετε από τους μαθητές να προσδιορίσουν την εξίσωση που περιγράφει τη γραφική παράσταση ή να καθορίσουν το πεδίο ορισμού και το σύνολο τιμών της συνάρτησης. Μπορείτε επίσης να συνεχίσετε ρωτώντας «Τι θα συμβεί αν;». Για το παράδειγμα του σολομού, τέτοιες ερωτήσεις θα μπορούσαν να περιλαμβάνουν
- Πώς θα έμοιαζε η γραφική παράσταση αν μαγειρεύαμε ένα μικρότερο κομμάτι σολομού; Ένα μεγαλύτερο;
- Πώς θα έμοιαζε η γραφική παράσταση αν βάζαμε ένα κατεψυγμένο κομμάτι σολομού;
- Πώς θα έμοιαζε η γραφική παράσταση αν αφήναμε τον σολομό περισσότερο στο φούρνο;
Η ενθάρρυνση των μαθητών να κάνουν τέτοιου είδους ερωτήσεις, τους εκπαιδεύει να εξερευνούν τα χαρακτηριστικά και τους περιορισμούς ενός μαθηματικού μοντέλου, και τους δείχνει πώς να σκέφτονται σαν μαθηματικοί.
Είναι επίσης αποτελεσματικό να εργάζεστε με πολλές ιστορίες γραφικών παραστάσεων συνεχόμενα. Με αυτόν τον τρόπο, μπορείτε να συγκρίνετε και να αντιπαραβάλλετε διαφορετικές γραφικές παραστάσεις και να κάνετε συνδέσεις μεταξύ διαφορετικών μαθηματικών εννοιών. Για παράδειγμα, η ιστορία «ταχύτητα ποδηλάτου» παρακινεί τους μαθητές να σχηματίσουν τη γραφική παράσταση της ταχύτητας ενός ποδηλάτου σα συνάρτηση του χρόνου, καθώς το ποδήλατο κατεβαίνει έναν λόφο, επιβραδύνεται και τελικά σταματά. Η γραφική παράσταση καταλήγει να είναι μια σχεδόν τέλεια παραβολή. Τι γίνεται όμως με τη γραφική παράσταση που περιγράφει την απόσταση που διανύθηκε ως συνάρτηση του χρόνου; Αυτή η ερώτηση απαντάται στη γραφική παράσταση της ιστορίας«απόσταση ποδηλάτου». Επιτρέποντας τους μαθητές να εργαστούν και με τις δύο αυτές γραφικές παραστάσεις ιστοριών, μπορούν να κάνουν συνδέσεις μεταξύ εννοιών όπως η παράγωγος και η παράγουσα συνάρτηση.
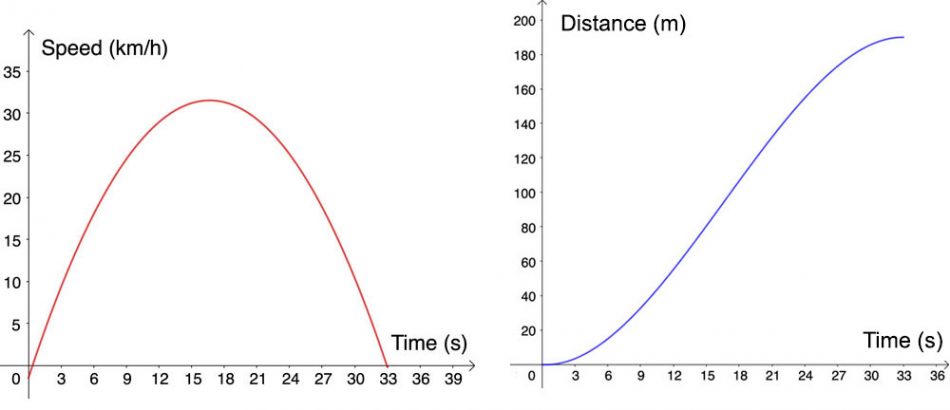
Η εικόνα είναι ευγενική προσφορά της Emelie Reuterswärd
Ως επέκταση, μπορείτε να αφήσετε τους μαθητές σας να δημιουργήσουν τις δικές τους γραφικές παραστάσεις ιστοριών χρησιμοποιώντας τα κινητά τους τηλέφωνα. Αυτό τους ενθαρρύνει να δουν τα μαθηματικά σε καθημερινά γεγονότα και να τα περιγράψουν με ένα μαθηματικό μοντέλο. Στη δευτεροβάθμια εκπαίδευση, οι ταινίες μπορούν να διερευνήσουν φαινόμενα σε άλλα μαθήματα, όπως φυσική ή επαγγελματικά μαθήματα. Με αυτόν τον τρόπο, οι ταινίες των μαθητών μπορούν να αποτελέσουν εφαλτήριο για μια διεπιστημονική μαθησιακή δραστηριότητα.
Γιατί να χρησιμοποιήσετε γραφικές παραστάσεις ιστοριών;
Υπάρχουν αρκετοί λόγοι για να δουλέψετε με γραφικές παραστάσεις ιστοριών.
- Οι μαθητές βιώνουν πώς χρησιμοποιούνται οι γραφικές παραστάσεις για να περιγράψουν καθημερινά φαινόμενα. Έτσι συνδέονται τα μαθηματικά με την καθημερινότητα των μαθητών και τους επιτρέπει να δουν τη χρησιμότητα των μαθηματικών.
- Η συζήτηση στην τάξη των γραφικών παραστάσεων των μαθητών δημιουργεί την ανάγκη να διατυπωθεί αυτό που έχουν σχεδιάσει οι μαθητές. Αυτό δίνει τη δυνατότητα να εισαχθούν σημαντικές έννοιες, όπως η κλίση, η γραμμική, η σταθερή,η αύξουσα και φθίνουσα (συνάρτηση). Στο λυκειο, μπορείτε να χρησιμοποιήσετε γραφικές παραστάσεις ιστοριών για να συζητήσετε πιο προχωρημένες έννοιες, όπως παραγώγους, σημείο καμπής και μέγιστο.
- Αφού δουλέψετε με αρκετές διαφορετικές γραφικές παραστάσεις ιστοριών, ένα φυσικό βήμα είναι να συγκρίνετε τις γραφικές παραστάσεις και να τις κατηγοριοποιήσετε. Έτσι, η δημιουργία γραφικών παραστάσεων ιστοριών είναι ένα εξαιρετικό εργαλείο για την εισαγωγή και την ονομασία σχέσεων, π.χ., γραμμικές, τετραγωνικές, περιοδικές και εκθετικές.
- Στο γυμνάσιο είναι σύνηθες να δουλεύουμε κυρίως με γραμμικές σχέσεις. Με τη βοήθεια γραφικών παραστάσεων ιστοριών, μπορείτε να δείξετε στους μαθητές ότι υπάρχουν και άλλα είδη σχέσεων, οι γραφικές παραστάσεις των οποίων δεν είναι ευθείες γραμμές.
- Η σχεδίαση γραφικών παραστάσεων καθημερινών γεγονότων είναι ένα κοινό θέμα σε πολλά σχολικά βιβλία. Επιτρέποντας στους μαθητές να δουν μια ταινία του γεγονότος, το κάνει πιο συγκεκριμένο, κάτι που μπορεί να διευκολύνει τους μαθητές να σχεδιάσουν τη γραφική παράσταση. Επιπλέον, η σύνδεση μεταξύ του γεγονότος και της γραφικής παράστασης γίνεται ισχυρότερη.
- Η σχεδίαση γραφικών παραστάσεων των καθημερινών γεγονότων είναι μια πρόκληση που συχνά μπορεί να αποκαλύψει κρυμμένες παρανοήσεις. Για παράδειγμα, οι μαθητές συχνά δυσκολεύονται να βρουν μια κατάλληλη κλίμακα και αποτυγχάνουν να τοποθετήσουν εξίσου τις ποσότητες κατά μήκος του άξονα. Το να χρειάζεται να εξηγούμε τα πράγματα και όχι απλώς να σχεδιάζουμε δεδομένα, μπορεί συχνά να αποκαλύψει κρυφές παρανοήσεις.
Το τελευταίο σημείο είναι ιδιαίτερα σημαντικό αυτής της προσέγγισης. Μια κοινή παρανόηση είναι οι λεγόμενες «εικονικές» αναπαραστάσεις γραφικών παραστάσεων. Αυτό σημαίνει ότι ο μαθητής βλέπει μια συσχέτιση μεταξύ του σχήματος της γραφικής παράστασης και ενός οπτικού χαρακτηριστικού του περιγραφόμενου γεγονότος. Για παράδειγμα, οι μαθητές που εργάζονται με την γραφική παράσταση της ιστορίας «ταχύτητα ποδηλάτου», μπορούν να σχεδιάσουν μία γραφική παράσταση που μοιάζει με το σχήμα της κοιλάδας που πέρασε το ποδήλατο (αριστερό γράφημα), αντί για μια παραβολή με ένα μέγιστο σημείο (δεξί γράφημα).
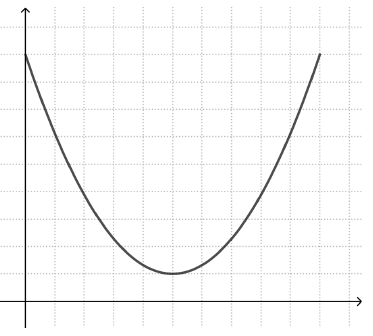
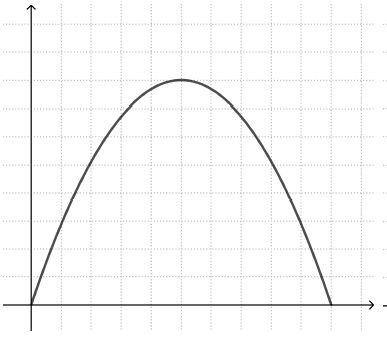
Παρόμοια, ένας μαθητής που προσπαθεί να σχεδιάσει μια γραφική παράσταση για το πως αλλάζει το ύψος μιας κινούμενης κούνιας με το χρόνο, μπορεί να σχεδιάσει μια γραφική παράσταση που μοιάζει με την κίνηση της κούνιας πίσω και εμπρός (αριστερό γράφημα), αντί για μία περιοδική γραφική παράσταση που εναλλάσσεται μεταξύ μέγιστων και ελάχιστων τιμών y (δεξί γράφημα).

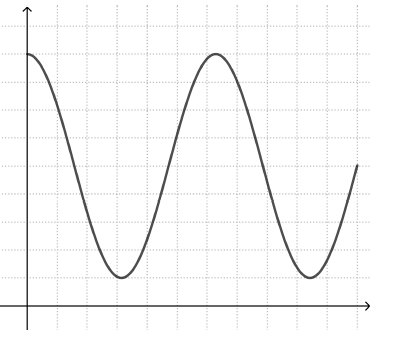
Η προσέγγιση της γραφικής παράστασης της ιστορίας κάνει ορατές τέτοιες παρανοήσεις και παρέχει εξαιρετικές ευκαιρίες στους μαθητές να τις συζητήσουν και να τις ξεπεράσουν.
Resources
- Διαβάστε περισσότερα για τη γραφική παράσταση ιστοριών και αποκτήστε πρόσβαση σε βίντεο με γραφικές παραστάσεις ιστοριών στο www.matemagi.com/graphingstories
- Εξηγήστε την εκθετική αύξηση στους μαθητές σας μέσω αυτών των απλών ασκήσεων:
- Vieser W (2021) Exponential growth 1: learn the basics from confetti to understand pandemics. Science in School 53.
- Δείτε την εκθετική αύξηση μέσω της εφεύρεσης του σκακιού και της εξάπλωσης μολυσματικών ασθενειών: Vieser W (2021) Exponential growth 2: real-life lessons from the COVID-19 pandemic. Science in School 53.
- Διαβάστε για τη σημασία της στατιστικής και της σωστής ανάλυσης δεδομένων: Le Guillou I (2021) Clinical trials count on more than statistics. Science in School 52.
- Εμπλέξτε τους μαθητές σας και κάντε θεμελιώδη φυσική με καθημερινά αντικείμενα: de Winter J (2022) Physics with everyday objects: springy sweets, a universe in your pocket, and drawing circuits. Science in School 56
Institutions
Science on StageReview
Αυτό το άρθρο αφορά τη δημιουργία γραφικών παραστάσεων ιστοριών. Οι μαθητές παρακολουθούν μια ταινία μικρού μήκους από ένα καθημερινό γεγονός, όπως ένα ποτήρι γεμάτο νερό, και καλούνται να σχεδιάσουν μία γραφική παράσταση του γεγονότος. Αυτά τα σκίτσα συζητώνται στην τάξη. Αυτή η προσέγγιση θα πρέπει να τους βοηθήσει να αναπτύξουν καλύτερη κατανόηση των εννοιών μιας γραφικής παράστασης. Έχει ενδιαφέρον ότι δεν εκφωνείται ούτε εμφανίζεται κείμενο στις ταινίες. Αυτό καθιστά αυτή την προσέγγιση ιδιαίτερα κατάλληλη για μαθητές με γλωσσικά μειονεκτήματα. Εάν ο εκπαιδευτικός δώσει προσοχή στο (μαθηματικό) λεξιλόγιο όταν συζητά τις γραφικές παραστάσεις, οι μαθητές μπορούν να βελτιώσουν, επιπλέον, και τις γλωσσικές τους δεξιότητες.
Annemiek van Leendert, Math teacher, Royal Visio, the Netherlands





