Hazañas increíbles: magia con monedas Teach article

Para realizar estos trucos, necesitará disponer de monedas y deberá emplear su conocimiento científico para comprender lo que sucede.

En este tercer artículo de hazañas increíbles, presentamos desafíos entretenidos que utilizan dinero y, desde luego, conocimientos de física. Para estas actividades, resultan especialmente útiles las monedas de un centavo de Estados Unidos y las monedas de aluminio de distintos países, por lo que si encuentra estas monedas durante sus vacaciones este verano, tal vez sea buena idea conservar algunas.

Hazaña 1: La moneda saltarina

¿Puede hacer que una moneda salte hacia adentro de una taza sin usar sus manos? Sorprendentemente, la respuesta es sí. Y se puede hacer tan solo con un soplido. El desafío es hacer que la moneda salte hacia adentro de la taza soplando lo suficientemente fuerte.

Luego de lograrlo, puede calcular la velocidad mínima del soplido que se necesita para que la moneda salte a la taza. También puede repetir el truco y los cálculos con otras monedas.

Materiales

• Una moneda pequeña y liviana, si es posible de aluminio (p. ej., el yen chino)
• Otras monedas pequeñas (opcional)
• Una caja pequeña de fósforos
• Una taza o un jarro, preferentemente con sus lados inclinados
• Una mesa u otra superficie nivelada

Procedimiento

1. Coloque la moneda, la caja de fósforos y la taza como lo indica la figura 1.
2. Ubíquese de manera que su soplido pueda ir derecho hacia la moneda, como se muestra en la figura 1.
3. Sople de manera rápida y enérgica. La moneda debería saltar hacia adentro de la taza (figura 2).
4. Si quiere divertirse más, en vez de la taza puede usar lápices apilados o acomodados uno junto a otro y las monedas pueden hacer un salto en alto o un salto en largo.

Discusión

¿Cómo hace una rápida bocanada de aire para levantar la moneda y enviarla dentro de la taza, si no hay nada que la empuje desde abajo? La explicación reside en el principio de Bernoulli, el mismo concepto que explica el impulso de las alas de las aeronaves hacia arriba al moverse rápidamente a través del aire. El principio indica que cuando la velocidad del aire (o de cualquier fluido) aumenta, su presión disminuye. Por ello, en este caso, el soplido rápido de aire causa una disminución de la presión del aire sobre la moneda, que la levanta hacia adentro de la taza.

Matemáticamente, el principio de Bernoulli se puede definir así:

P + ½ ∂ v² = constante

constante:

P = presión (fuerza ejercida, dividida por el área sobre la cual se la ejerce)

∂ = densidad del fluido (aire)

v = velocidad del objeto o fluido que se mueve

Por eso,

P₁ + ½ ∂ v₀² = P₂ + ½ ∂ v²

La diferencia de presión entre el aire en estado estacionario (v₀ = 0) y el aire móvil (v) es la siguiente:

P₁ – P₂ = ½ ∂ v²

La fuerza de elevación debido a la disminución de la presión es:

(P₁ – P₂) x A (donde A = área de la moneda)

= A x ½ ∂ v² (desde arriba)

La fuerza necesaria para levantar la moneda es m × g (donde m = masa de la moneda y g = aceleración debido a la gravedad, aproximadamente 9,8 m s^–2)

Esto significa que el peso de la moneda está equilibrado cuando 

½ ∂ v² x A = m x g

Entonces, podemos calcular la velocidad mínima (v_min) del soplido que se necesita para levantar la moneda:

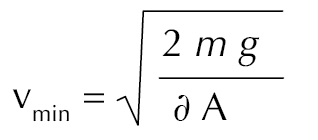
Para monedas circulares, A = πr²

Para un yen chino (masa = aproximadamente 1 g, diámetro = 20 mm)

Densidad del aire = 1.225 kg/m³

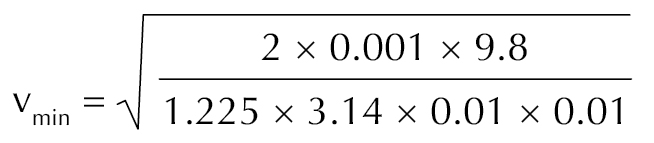
= 7.2 m/s

Para una moneda de un centavo de euro (masa = 2,3 g, diámetro 16,25 mm)

= 13.32 m/s

Para una moneda de cinco centavos de euro (masa = 3,9 g, diámetro 21,25 mm)

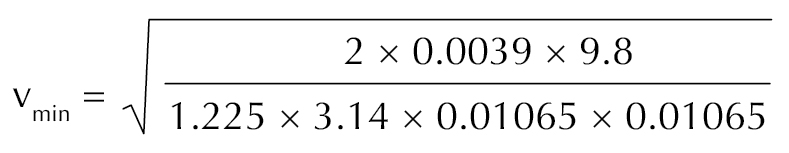
= 13.23 m/s

Observe que estos dos últimos valores son muy similares. ¿Puede demostrar que las monedas del mismo grosor y del mismo material tendrán la misma velocidad de elevación sin importar su diámetro?

Hazaña 2:  Acumulación de agua

Esta hazaña está relacionada con otra propiedad de los fluidos: la tensión superficial. Usamos una moneda como base sobre la que acumulamos agua. El desafío es colocar la mayor cantidad de gotas de agua no contaminada de un cuentagotas sobre una moneda limpia sin derramarla por fuera del borde de la moneda. Puede llevar a cabo este desafío a modo de competencia para determinar quién coloca la mayor cantidad de gotas sobre la moneda, pero asegúrese de que todos tengan el mismo tamaño de monedas y de cuentagotas.

Materiales

Cada persona o grupo necesitará:

• Una moneda pequeña de cobre (una moneda de un centavo de euro es ideal)
• Un cuentagotas (p. ej., una pipeta o una jeringa)
• Agua limpia
• Una mesa u otra superficie nivelada

Procedimiento

1. La mayoría de las monedas en uso están algo grasientas, así que primero lave la moneda con agua caliente y jabón, luego enjuáguela y séquela bien. También debe quitar completamente el jabón o detergente.
2. Llene el cuentagotas con agua limpia.
3. Sostenga el cuentagotas sobre la moneda (sin que la toque) y coloque una gota de agua sobre ella (figura 3).
4. Siga colocando gotas de agua sobre la moneda y contando la cantidad de gotas mientras las coloca. El agua se acumulará sobre la superficie de la moneda, pero finalmente se derramará. Observe cuántas gotas agregó antes de que se derramara (figura 4).
5. ¿Cuál es la mayor cantidad de gotas que puede colocar sobre la moneda? Vuelva a realizar este desafío para calcular el mejor valor que obtiene, o averigüe el que lograron los demás e intente ganarles.
6. Si quiere un mayor desafío, intente descubrir qué pasa si agrega jabón o detergente al agua sobre la moneda. Piense y anote lo que cree que pasará. Luego, con cuidado, haga que un trozo de jabón o una gota de detergente toque el agua. ¿Qué sucede y por qué?

Discusión

Debería ser posible poner alrededor de 40 gotas sobre una moneda limpia, aunque este número varía considerablemente de acuerdo a la pureza del agua y al tamaño de la moneda. Pero si el agua es un líquido, ¿cómo permanece sobre la moneda en vez de derramarse?

La respuesta, por supuesto, está en la tensión superficial: las fuerzas de atracción entre las moléculas del agua actúan como un tejido que sostiene el agua sobre la moneda. Aunque estas fuerzas son algo débiles, realmente afectan la manera en que se comportan los líquidos, tal como demuestra esta actividad. La tensión superficial también es lo que causa que las gotas de un líquido tomen una forma esférica, lo que reduce al mínimo la superficie que ocupa. 

Sin embargo, la suciedad sobre la superficie de la moneda puede reducir la tensión superficial del agua que se coloca, lo que hace que se puedan agregar menos gotas: el agua no se acumula, sino que se extiende por toda la superficie. Y cuando el agua está contaminada con jabón o detergente, se reducen considerablemente las fuerzas de la tensión superficial. Como las gotas ya no se mantienen unidas, solo se pueden colocar unas pocas gotas sobre la moneda antes de que se derramen fuera del borde.

Hazaña 3: Cara o cruz

Esta actividad no es realmente un desafío físico, pero sí nos lleva a cuestionar la existencia de una moneda «justa».

Sabemos que las monedas tienen dos lados (cara y cruz) y que la probabilidad de que una moneda caiga de un lado en particular (por ejemplo, cara) es del 50 %. Aunque esta suposición está muy extendida y en ella se basan distintas situaciones (desde el comienzo de un partido de fútbol hasta preguntas de probabilidad en matemáticas), ¿es realmente cierta en la práctica?

Para la mayoría de las monedas, la respuesta es probablemente «sí, casi siempre», pero no es cierto para todas las monedas. Particularmente, las monedas estadounidenses de un centavo no tienen el mismo peso a ambos lados: el reverso (la cruz) es más pesado que el frente (la cara). Esto significa que, luego de arrojar la moneda sin efectos ni trucos especiales, estas monedas caerán del lado de la cara (con el frente hacia arriba) con más frecuencia que del lado de la cruz. 

En esta actividad, usamos un método ingenioso que invita a arrojar 50 monedas al mismo tiempo y revela si ese tipo de moneda es una moneda justa o no.

Materiales

• Un gran número (p. ej. 50) de monedas idénticas de poco valor, preferentemente monedas estadounidenses de un centavo.
• Una mesa u otra superficie nivelada.

Procedimiento

1. Coloque las monedas sobre la mesa.
2. Una a una, logre que las monedas hagan equilibrio sobre su borde y colóquelas en diferentes direcciones (figura 5).
3. Una vez que todas las monedas están «paradas», golpee bruscamente la mesa con el puño (figura 6). Las monedas caerán de costado, con la cara o cruz para arriba.
4. Agrupe las monedas que cayeron de cara y las que cayeron de cruz (figura 7). ¿Cuántas hay en cada grupo? ¿Piensa que la moneda es justa o no?
5. Si es posible, repita la actividad con otro grupo de monedas de diferente denominación. Si va a viajar al extranjero para las vacaciones de verano, trate de traer algunas monedas.

Discusión

Arrojar una moneda, como se hace al comienzo de un partido de fútbol, no demuestra si la moneda es justa o no, ya que la manera en la que se arroja la moneda tiene más efecto sobre cómo cae que cualquier leve diferencia de masa entre los dos lados. El desafío es arrojar la moneda sin darle efectos y así darle la posibilidad de caer de cualquier lado (si está verdaderamente equilibrada). En esta actividad lo hacemos al colocar aproximadamente 50 monedas sobre los bordes y observar cuántas caen de un lado o de otro.

Si tiene la suerte de tener un conjunto de monedas estadounidenses de un centavo, seguramente puede observar que esta moneda aparentemente normal no es muy justa. Si le interesa la probabilidad y la estadística, puede proponer y contestar estas preguntas con sus estudiantes, como por ejemplo:

• ¿Cuál es la probabilidad de que el resultado (cuántas veces resulta cara o cruz) ocurra solo por casualidad?
• ¿Es el resultado estadísticamente significativo? (Considere un nivel de significación de p < 0,05).
• ¿A partir del resultado, puede calcular la probabilidad de que arrojar la moneda una sola vez caiga (i) cara o (ii) cruz?

Por lo que sabemos, basados en nuestros experimentos, no hay otra moneda (además del centavo estadounidense) que tenga la suficiente diferencia de masa que permita observar este efecto de manera confiable. Aquí hay un desafío más: tras obtener monedas de distintos países del mundo y repetir este experimento, ¿puede encontrar otras monedas que no estén lo suficientemente equilibradas? Si encuentra alguna, por favor escríbanos para contarnos.

Download

Download this article as a PDF