Com podem modelar el canvi climàtic a classe Teach article
Traduït per Jordi Salat. Per què no animeu els vostres estudiants a fer les seves pròpies prediccions sobre el canvi climàtic? Dudley Shallcross i Tim Harrison de la Universitat de Bristol, Regne Unit, us hi ajudaran.
El canvi climàtic i l’escalfament global són temes ‘candents’ que mereixen un lloc important als temaris científics de les escoles. Però, com podem predir com evolucionarà el nostre clima? Potser fóra un bon moment per introduir els nostres alumnes en el món del models climàtics, començant pels més senzills. En aquest article mostrarem com podem investigar els factors més destacats que afecten el clima de Terra amb un simple full de càlcul.
Un primer intent de modelar el clima
El model de clima més senzill consisteix en plantejar que l’energia solar captada pel planeta sigui igual a l’energia terrestre emesa cap a l’espai , és a dir, un model on ‘tota l’energia que entra torna a sortir’. Val a dir que en aquest article quan parlem d’energia ens referim realment a ‘flux d’energia’, o sigui, energia per unitat de temps. A partir de diverses mesures sabem que l’energia (per segon) solar que arriba a les capes altes de l’atmosfera, el què es coneix com constant solar S, és de 1370 Wm-2.
Podem començar calculant la temperatura mitjana de la Terra, TE, amb aquest senzill model. Prenguem el radi RE, d’una Terra perfectament esfèrica, aleshores podrem veure que la Terra capta la radiació solar a través d’una àrea que fa πRE2 (equivalent a un disc pla) però retorna l’energia a través de tota la seva superfície, és a dir, una àrea de 4πRE2.
(a) Energia que entra = energia que surt
i, d’acord amb la Llei de Stefan-Boltzmann (vegi’s el requadre)
(b) Per unitat de temps, energia per unitat de superfície x àrea total(disc) = energia per unitat de superfície x àrea total(sphere)
(c) 1370 x πRE2 = σTE4 x 4πRE2
Reordenant les equacions, tenim:
σTE4 = 1370 = S/4
4
TE4 = 1370
(4 x 5.67 x 10-8)
TE = 279 K (6 °C)
on σ és la constant de Stefan-Boltzmann (5.67 x 10-8 Wm-2K-4).
A primer cop d’ull, i malgrat venir d’un model tan rudimentari, sembla un valor prou raonable. En realitat però, el valor mitjà estimat de la superfície de la Terra és de 16 °C. (Hi ha diverses maneres d’aconseguir afinar més, com ara descompondre la Terra en franges de latitud constant, calcular temperatura mitjana per franja, sumar i promitjar). El problema amb aquest model tan senzill, no obstant, és que part de l’energia solar no s’absorbeix si no que és reflectida novament a l’espai pels núvols i el glaç.
Aproximadament un 24% de l’energia incident és reflectida pels núvols i un altre 6% per la superfície terrestre, per exemple, pel glaç. Així doncs, la reflectivitat total de la Terra – anomenada albedo (A) – és del 30% ó 0.3. Per tant, el membre de l’esquerra de l’equació (c), queda com 0.7 x 1370 x πRE2 i el càlcul de TE ve donat per:
TE4 = 1370 x 0.7
(4 x 5.67 x 10-8)
TE = 255 K (-18 °C)
Valor que és massa baix de bon tros, i que ens porta a preguntar-nos: per què la Terra és tan càlida? De cara a respondre la pregunta caldrà un model un xic més complex.
Elements bàsics de física
Radiació d’un cos negre i Llei de Stefan-Boltzmann
Tot cos emet energia en forma de radiació electromagnètica. Un cos negre absorbeix tota la radiació incident i la radiació que emet és funció de la seva temperatura de superfície.
La Llei de Stefan-Boltzmann relaciona l’energia total, I, que emet un cos negre amb la temperatura, T, segons:
I(T) = σT4 (Equació 1)
on:
I és l’energia emesa per unitat de superfície emesa en un segon (Wm-2)
T és la temperatura absoluta (K)
σ és la constant de Stefan-Boltzmann (5.67 x 10-8 Wm-2K-4).
El model d’una capa atmosfèrica
Si suposem que l’atmosfera està formada per una única capa de gasos diversos, podem crear un model, més ajustat que el primer, que els estudiants podran fer servir amb l’ajut d’un full de càlcul. En aquest model es tindrà en compte l’absorció per part de l’atmosfera de la llum visible que arriba del Sol i la infraroja que emet la Terra.
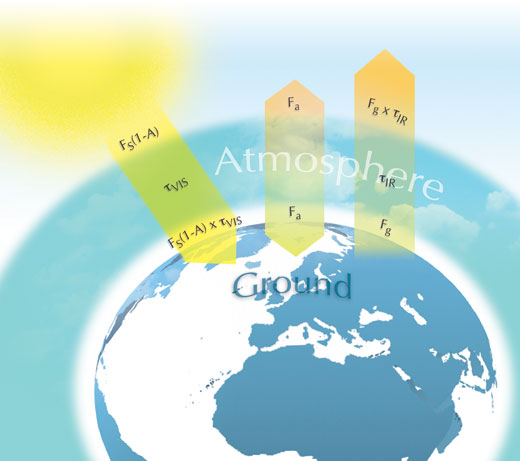
En la figura inferior es mostren els elements del model. FS és la constant solar dividida per 4 (S/4), que incorpora la diferència entre la superfície del disc, πr2, on es reparteix l’energia incident, and la superfície de la esfera, 4πr2 que emet l’energia radiant (el fonament del primer model). L’energia que arriba del Sol és, per tant, FSon A és l’albedo – el percentatge reflectit novament cap a l’espai. Aquesta energia incident es troba en les regions visible i UV de l’espectre. τVIS és la fracció d’energia incident que no s’absorbeix en l’atmosfera: si l’atmosfera l’absorbeix tota, τVIS valdrà zero; i si no n’absorbeix gens, τVIS serà 1. Així doncs, l’energia que arribarà finalment a la superfície del planeta serà FS(1-A) x τVIS.
Suposem que la Terra actua com un cos negre i anomenem Fg a l’energia que emet a través de la seva superfície. Aquesta radiació terrestre està centrada en la regió infraroja de l’espectre. A l’atmosfera hi ha certs gasos (els anomenats d’efecte hivernacle) que absorbeixen l’energia de la radiació infraroja. Si, de manera similar a τVIS, definim τIR com la fracció d’energia infra-roja no absorbida per aquests gasos, l’energia que se’n va serà Fg x τIR.
Si anomenem Fa a l’energia dins l’atmosfera i assumim que tant l’energia que entra i surt al cim de l’atmosfera com a la superfície de la Terra es compensen, aleshores:
a la superfície de la Terra:
FS(1-A) x τVIS + Fa = Fg (Equació 2)
al cim de l’atmosfera:
Fg x τIR + Fa = FS(1-A) (Equació 3)
Combinant les equacions 2 i 3 dóna:
Fg = FS(1-A)(1 + τVIS)
(1 + τIR)
Finalment,
Fg = σTE4 = FS(1-A)(1 + τVIS)
(1 + tIR)
TE = [ FS(1-A)(1 + τVIS) ]0.25
[ σ(1 + τIR) ] (Equació 4)
Si prenem els següents valors:
FS = 1370/4 = 342.5 Wm-2 (la constant solar dividida per 4)
A = 0.3
τVIS = 0.8
τIR = 0.1
L’equació 4 ens dóna:
TE = 288.5 K (15.5 °C),
que és una bona aproximació al valor actual de la temperatura mitjana de la superfície de la Terra.
Aquesta Equació 4 és la que pot introduir-se en un programa o full de càlcul, com Microsoft Excel, per permetre que els estudiants puguin experimentar la resposta de la temperatura global en canviar els paràmetres de l’equació. Això és el què s’ha fet i se’n pot trobar una versió interactiva, que també es pot descarregar, en el web de la Universitat de Bristolw1.
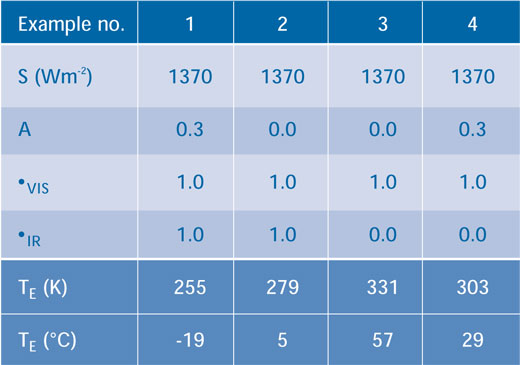
A la Taula 1 es mostren exemples dels resultats que s’obtenen modificant les variables A, τVIS and τIR are altered. L’Exemple 1, que dóna una temperatura de 255 K, suposa que l’albedo és 0.3 i que l’atmosfera no absorbeix cap dels fluxos d’energia, ni dels rebuts ni dels emesos (és a dir que, tant τVIS com τIR valen 1.0). En l’Exemple 2 veiem que la temperatura de la Terra ha augmentat fins a 279 K, quan hi traiem els núvols i el gel (A = 0.0), cosa que mostra la importància que té l’albedo. En l’Exemple 3, tampoc no hi ha ni núvols ni gel (A = 0.0) però l’atmosfera absorbeix tota la radiació infraroja emesa (és a dir τIR = 0.0) i la Terra s’escalfa fins els 331 K. Si ara hi introduïm les núvols i el gel, en l’Exemple 4 (A = 0.3), la temperatura decau fins els 303 K.
Possibles preguntes
Algunes típiques preguntes que es podrien fer, i que obligarien als estudiants a utilitzar el model, són
- Quina de les variables té un impacte més gran en la temperatura global?
- Si la distància mitja de la Terra al Sol augmentés un 1%, la constant solar es reduiria segons un factor de l.0201, és a dir, valdria 1343 Wm-2. Quina temperatura trobaríem? Considera un albedo de 0.3, un τIR 0.3 i un τVIS de 0.6.
(La constant solar varia amb el quadrat de la distància al Sol, per tant, en desplaçar la Terra un 10% més a prop del Sol, tindrem S = 1370/(0.9)2 = 1691 Wm-2 i en moure-la un 1% més enllà, S = 1370/(1.01)2 = 1343 Wm-2)
Per descomptat, es poden preguntar coses força més engrescadores com
- Si la sorra del Sahara es pogués convertir en un mirall de vidre (al cap i a la fi el vidre s’obté fonent sorra),
- Com hauria de ser de gran el mirall per refredar el planeta 1 °C?
- Quina fracció del desert representaria?
Un model més sofisticat
Com podria es comparar aquest senzill model climàtic amb els més sofisticats, com el del Hadley Centre, emprat pel Servei Meteorològic del Regne Unit (veure imatge de sota)?De fet, els dos models són molt similars en tot, excepte que el del Hadley Centre enlloc de considerar l’atmosfera d’una sola capa, la subdivideix en un cert nombre de caixes, d’acord amb l’altitud, latitud i longitud. Per cada caixa, el model calcula directament les quantitats de radiació incident UV/visible transmesa i absorbida, i de radiació infra-roja transmesa per la caixa de retorn, d’acord amb les concentracions de determinats gasos d’efecte hivernacle, de la superfície de núvols i de glaç. Les versions més sofisticades del model del Hadley Centre també consideren els fluxos de calor que entren i surten de l’oceà, i l’absorció de CO2 per part de la vegetació. De tota manera, si sou capaços d’entendre els principis de funcionament del model senzill, estareu encarrilats per comprendre els models més complicats del clima real.
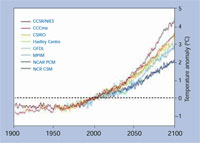
Prediccions d’escalfament global
en relació a la temperatura mitjana
global del 2000 a través del model
climàtic. Les dades del model estan
extretes del Centre de Distribució
de Dades del Grup
Intergovernamental d’Experts sobre
el Canvi Climàtic. Fer clic sobre la
imatge per ampliar-la
Imatge cortesia de Robert A. Rohde;
font: Wikimedia Commons
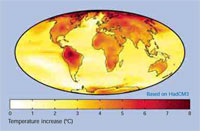
predicció del 2070-2100 vs.
valors mitjans de 1960-1990 Mapa
d’escalfament global previst pel
final del segle XXI, utilitzant el
model climàtic HADCM3 del Hadley
Centre que preveu un escalfament
mitjà de 3.0°. Fer clic sobre la
imatge per ampliar-la
Imatge cortesia de Robert A.
Rohde; font: Wikimedia Commons
Prenent part en una simulació de clima real
Climateprediction.netw2 és l’experiment més gran pensat per fer proves i predir el clima al segle 21. Consisteix en obtenir la col·laboració de tothom que pugui oferir temps d’ordenador – com quan el tenim engegat però no el fem servir a la seva màxima capacitat. El model complet de clima té molts paràmetres que cal ajustar a través d’un nombre elevat de simulacions. Tot i els recursos computacionals disponibles per l’equip de climateprediction.net, un nombre tan gran de simulacions suposaria molt de temps. La idea que hi ha darrera climateprediction.net és que cadascú pugui descarregar-se una versió del model que pugui explorar un d’aquests paràmetres en particular (preseleccionat). El model tardaria uns tres mesos funcionant en un segon pla sense comprometre la velocitat de l’ordenador mentre estem treballant.
Els càlculs es realitzen en tres parts. En la primera es fan els càlculs amb les dades des del 1850 al 1900, comprovant les previsions obtingudes amb les registres de temperatura, en el què es coneix com fase de calibració. La segona part fa una simulació a partir del 1901 fins el moment actual. El tercer pas consisteix en fer una simulació del clima futur (2000-2100) amb un paràmetre canviat, per exemple la sensibilitat del clima a les incerteses sobre el cicle del sofre. Tan bon punt els càlculs s’han completat, les dades són incorporades al Servei Meteorològic del Regne Unit. El programa proporcionat (gratuïtament) amb la simulació ofereix a l’usuari un gràfic amb els canvis climàtics a mesura que es van calculant. Les variacions de temperatura segons l’estació de l’any, latitud, longitud i altitud representen només algunes de les variables que s’hi poden visualitzar. Aquestes característiques poden permetre a les escoles preparar projectes transversals que relacionin geografia i ciències físiques.
Al següent número de Science in School, els autors suggereixen alguns experiments de química rellevants pel canvi climàtic.
Web References
- w1 – Una versió interactiva del model climàtic senzill per treballar en xarxa o descarregar-se a: www.chemlabs.bris.ac.uk/outreach/resources/simple_climate_model/index.html
- Utilitzeu els cursors per canviar les variables.
- w2 – Per més detalls sobre l’experiment i com participar-hi, consulteu http://climateprediction.net.
- El web climateprediction.net també ofereix informació i recursos específics per les escoles, disponibles en anglès i espanyol: http://climateprediction.net/content/resources-schools
Resources
- Harrison T, Shallcross D, Henshaw S (2006) Detecting CO2 – the hunt for greenhouse-gas emissions. Chemistry Review 15: 27-30
- Pacala S, Socolow R (2004) Stabilisation wedges: solving the climate problem for the next 50 years with current technologies. Science 305: 968-972. doi: 10.1126/science.1100103
- Shallcross D (2006) Dirty Air. Education in Chemistry, 43 (5): 131-135
- A l’adreça: www.chemlabs.bristol.ac.uk/outreach/resources/Atmos.html hi trobareu moltes notes sobre contaminació de l’aire, canvi climàtic i depleció de la capa d’ozó, útils per mestres i educadors.
- A l’adreça: www.grida.no/climate/vital/index.htm hi trobareu una font excel·lent de dades i gràfics relacionats amb el canvi climàtic.
- A l’adreça: www.cmdl.noaa.gov hi podeu trobar dades de l’Estació de Seguiment Global del Laboratori de Recerca del Sistema Terra.
- El web del Grup Intergovernamental d’Experts sobre el Canvi Climàtic, del qual es poden obtenir l’informe del 2007 i altres dades, és: www.ipcc.ch
- Haubold B (2008) An Inconvenient Truth. Science in School 9: 72. www.scienceinschool.org/2008/issue9/inconvenient
Review
El canvi climàtic ha de ser sens dubte un dels temes fonamentals en tots els nivells d’ensenyament de les ciències a les escoles de tot Europa. En particular, després del reconeixement internacional de la gran campanya sobre la Veritat Incòmoda d’Al Gore. Malgrat tot, els materials i la informació bàsica útil per professors de ciències, no sempre està disponible fàcilment. Aquest article en dues parts, no obstant, ofereix una visió adequada i fàcilment adaptable al complicat procés de modelar els processos atmosfèrics.
Tot i que el model matemàtic és el més adequat per utilitzar en cursos de ciències avançats per estudiants de 16 o més anys, els fenòmens bàsics poden presentar-se fàcilment a estudiants de 15 o menys anys – encara que no tinguin previst especialitzar-se en ciències més endavant. Els webs mencionats ofereixen un ventall ampli de recursos, imatges, gràfics i programes interactius, per abordar el tema, útils per tot professor de ciències.
Tobias Kirschbaum, Alemània





