Salvar a Terra à Hollywood Teach article
Desafie os seus alunos a salvar a Terra de uma colisão com um asteróide recorrendo a cálculos baseados no filme de ficção científica de Hollywood, Armageddon.
Que preferirão os alunos discutir? Filmes de Hollywood ou Física? Nas minhas aulas de Física tento combinar ambos os temas recorrendo a cenários de filmes de ficção científica de Hollywood como fonte para a resolução de exercícios (problemas) – de forma semelhante a utilizar as aventuras de super-heróis (ver Follows, 2017). Mesmo que os estudantes não tenham visto os filmes, continuam, aparentemente, a gostar de se embrenhar nos cenários originais e fantásticos que podem usar como base para fazer ciência a sério – logo que as ideias e os pressupostos sejam claramente demarcados.

geralt/pixabay.com
Neste artigo apresento alguns exercícios baseados no filme ‘Armageddon’ (1998) – um filme de Hollywood sobre uma missão heróica para salvar a Terra de um asteróide gigante que se dirige à mesma diretamente. O filme foi criticado por ser pouco realista mas, mesmo assim, oferece uma trama interessante para usar como base para os cálculos.
Armageddon: a história
No filme, os astrónomos descobrem um asteróide do tamanho do Texas que se dirige para a Terra, apenas 18 dias antes do impacto. Um plano é elaborado para detonar uma ogiva nuclear debaixo da superfície do asteróide, de forma a dividi-lo em duas metades iguais ao longo de uma falha. As duas metades deslocar-se-iam depois separadamente – falhando a Terra. De forma a executar o plano, a NASA enviou o furador de poços de petróleo Harry Stamper (Bruce Willis) e a sua equipa para o asteróide em dois vaivéns, que se deslocam primeiro em torno da Lua, surgindo depois atrás do asteróide. Assim que lá chegam, para evitar um desastre, têm de detonar a bomba antes do asteróide chegar à ‘barreira zero’, um ponto onde o asteróide chega oito horas depois de passar pela Lua.
Criando uma atividade em sala de aula
Os alunos podem efetuar uma variedade de cálculos baseados na informação que consta no filme, suplementada por alguns pressupostos razoáveis. A diversão reside em ver se as quantidades e pressupostos constantes no filme fazem sentido – ou não.
Do filme, sabemos que:
- O asteróide é do ‘tamanho do Texas’. Assumamos que isto se refere à área seccional através do centro de um asteróide aproximadamente esférico.
- O asteróide dirige-se para a Terra a uma velocidade de 22 000 milhas por hora.
- Cada metade do asteróide falha a superfície da Terra por 400 milhas (640 km).
Outra informação que precisamos:
- O Texas tem uma área de 696 200 km2.
- A densidade média dos quatro maiores asteróides conhecidos é de 2760 kg m-3. (Para comparação, a Terra tem uma densidade de 5520 kg m-3.)
- A distância da Terra à Lua é de 384 400 km.
- A Terra tem um raio de 6400 km.
- A energia de uma ogiva nuclear é de até 50 megatoneladas de TNT. (Esta é a energia da arma termonuclear mais poderosa conhecida: a ogiva Soviética chamada de ‘Big Ivan’.)
- 1 megatonelada de TNT são 4.18 x 1015 J
Assumamos que:
- O asteróide se dirige para o centro da Terra, de forma a ambas as metades do asteróide terem de se deslocar ‘de lado’ na mesma distância.
Questões para os alunos e cálculos trabalhados
Aos alunos pede-se que investiguem se o plano tem probabilidade de sucesso no salvamento da Terra da colisão. Isto pode ser efetivado numa sequência de cálculos, mostrados no que segue. Os alunos trabalham em grupo e são encorajados a discutir o percurso a seguir uns com os outros.
1. Mostrar que o asteróide tem um raio de 470.8 km.
Assumimos que a secção aproximadamente circular do asteróide tem uma área A igual à do Texas, ou seja, aproximadamente 696 200 km2.
A = πr2 onde r = raio do asteróide.
Assim:

2. A que velocidade se desloca o asteróide em unidades métricas (ou seja, em m s-1)?
Incentive os alunos a efetuar uma mudança de unidades formal:
22 000 milhas por hora (mph)
= 22 000 x 1609 m/3600 s
= 9833 m s-1
3. Quão longe da Terra está a ‘barreira zero’?
Para responder a esta questão, primeiro precisamos de descobrir a distância percorrida pelo asteróide em oito horas, uma vez que a ‘barreira zero’ é a distância equivalente a oito horas de viagem da Lua:
Distância = velocidade tempo
= 9833 m s-1 x 8 x 3600 s
= 2.83 x 108 m
Depois, subtraimos esta distância da distância total Terra-Lua (3.84 x 108 m) para calcular quanto mais longe terá o asteróide de viajar para colidir com a Terra.
3.84 x 108 m – 2.83 x 108 m
= 1.01 x 108 m
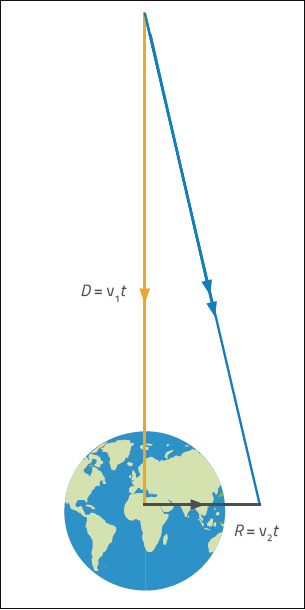
linha amarela mostra a
direção original da viagem do
asteróide. A linha preta
mostra quão longe tem de se
deslocar cada metade do
asteróide de forma a falhar a
Terra por 640 km; a linha
azul mostra o percurso
resultante que cada metade
de asteróide deve fazer.
Mike Follows/Nicola Graf
4. Quão depressa terão de se afastar os dois pedaços do asteróide um do outro de forma a evitar impacto com a Terra?
As duas metades do asteróide têm de viajar 1.01 108 m desde a ‘barreira zero’ de forma a atingir a Terra. Durante o tempo que isto leva, cada metade do asteróide também deve deslocar-se numa direção perpendicular à direção original, longe o suficiente para falhar a Terra por, pelo menos, 640 km em cada lado (ver a figura 1).
Aqui:
D = distância entre a ‘barreira zero’ e a Terra
R = raio da Terra mais os 640 km em quanto cada metade falha a Terra
v1 = velocidade do asteróide ao deslocar-se em direção à Terra
v2 = velocidade perpendicular de cada metade do asteróide que é necessária de forma a que falhe a Terra numa margem de 640 km
A velocidade v2 pode ser calculada de duas formas.
Método 1
Em primeiro lugar, calculamos o tempo (t) que o asteróide levaria desde a ‘barreira zero’ até à Terra:
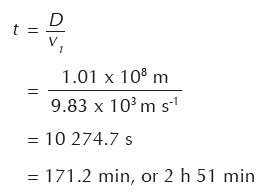
Podemos, agora, calcular a velocidade com que cada metade do asteróide se tem de deslocar numa direção perpendicular ao seu percurso original de forma a falhar a Terra numa margem de 640 km.
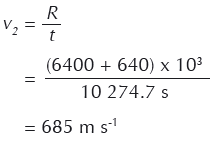
Método 2
Para aqueles alunos mais à vontade com a Matemática, podemos usar a proporcionalidade. Como no método acima, durante o tempo t que o asteróide leva a viajar 101 000 km em direção à Terra, as suas duas metades devem afastar-se de uma distância equivalente ao raio da Terra mais 640 km, R. Assim, recorrendo à Álgebra:

5. Qual é a massa do asteróide (assumindo que tem a densidade típica dos asteróides)?
A massa m é igual à densidade r vezes o volume V, pelo que m = r x V
O asteróide é aproximadamente esférico, pelo que V = 4 ⁄ 3 π R3
Da questão 1, R = 470.8 km
Assim M = ρπR3
= 2760 kg m-3 x 4/3 π x (4.71 x 105 m)3
= 1.21 x 1021 kg
6. Quanta energia cinética deve ser fornecida às duas metades do asteróide de forma a evitar a sua colisão com a Terra?
Nota: vai obter a mesma resposta quer o asteróide seja tratado como um conjunto ou como duas partes separadas.
E = 1/2 mv2
= 1/2 x 1.2 x 1021 kg x (685 m s-1)2
= 2.84 x 1026 J
7. Quantas armas nucleares do mesmo tamanho que o Big Ivan serão necessárias para fornecer esta energia?
Um Big Ivan é equivalente a 50 megatoneladas de TNT
= 50 x 4.18 x 1015 J
= 2.09 x 1017 J
Assim, a energia requerida para alterar o percurso do asteróide o suficiente para falhar a Terra é equivalente a:
![]()
8. Quão depressa se afastarão as duas metades do asteróide uma da outra se apenas uma bomba Big Ivan for usada?
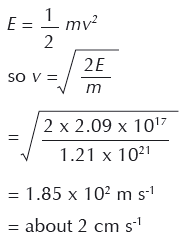
9. Quão longe estarão as duas metades uma da outra quando colidirem com a Terra, se apenas uma bomba Big Ivan for usada?
Já mostrámos (na questão 4) que na barreira zero o asteróide está a menos de três horas do impacto. A uma velocidade de 1.85 x 102 m s-1(questão 8), durante esse tempo cada metade do asteróide afastou-se 190 m do seu percurso original, pelo que as duas metades separam-se por menos de 400 m – demasiado pouco para evitar uma colisão com a Terra. De facto, dentro das circunstâncias descritas no filme, a equipa necessitaria de intercetar o asteróide quando ele estivesse a 74 x 1012 km – 25 vezes a distância do Sol à Terra, no espaço entre as órbitas de Urano e Neptuno.
Tudo isto serve para demonstrar que há alturas em que necessitamos de algo ainda maior do que uma explosão nuclear para fazer com que aconteçam coisas.

Jack W. Aeby (domínio público)/Wikimedia Commons
Discussão
Há muito mais aqui para discutir com os alunos, depois ou durante os cálculos. Os alunos podem bem ter as suas próprias ideias em como tornar o cenário mais realista – e em quais os resultados ou assunções são os mais absurdos. Por exemplo, porque falharam os cientistas a deteção do asteróide antes de estar tão próximo? E, apesar deste falhanço, como descobriram que tinha uma linha de falha através dele, exatamente alinhada com a direção do seu movimento?
Aqui vão algumas sugestões de outros pontos a considerar:
- Os cálculos não incluiram a energia necessária para separar as ligações químicas de forma a dividir o asteróide em dois: apenas foi incluída a energia necessária para afastar as duas metades, assumindo que o asteróide já estava convenientemente fraturado. Se adicionássemos a energia necessária para fraturar o asteróide, em quanto isto afetaria os cálculos?
- Se o asteróide atingisse a Terra, qual seria a energia do impacto? Os alunos podem calcular isto a partir da energia cinética do asteróide. Vão descobrir que o impacto com a Terra libertaria 5.8 x 1028 J – equivalente a 276 biliões (2.76 x1011) de Big Ivans. Por comparação, o asteróide que assinalou o final do Cretácio (e o desaparecimento dos dinossauros) há 65 milhões de anos é estimado ter soltado apenas 4 x 1023 J (2 milhões de Big Ivans).
- Os alunos podem investigar objetos reais que possam atingir a Terra e determinar quão típico é o asteróide do Armageddon comparado com asteróides em geral. A 9833 m s-1, a sua velocidade é mais baixa do que a média dos asteróides, que tem de valor 25 000 m s-1. (Por comparação, o cometa Halley tem uma velocidade de 53 600 m s-1 quando mais próximo ao Sol, no periélio.) O program NEO (near-Earth object) da NASAw1 procura por e segue objetos que possam atingir a Terra: um candidato é o asteróide (29075) 1950 DA que tem um diâmetro de cerca de 1 km. A probabilidade de atingir a Terra em 2880 é, no presente, estimada em 1 em 300.

References
- Follows M (2017) Heroes and villains: the science of superheroes. Science in School 40: 57-63.
Web References
- w1 – Para ler as últimas notícias do Center for Near Earth Object Studies, visite o site da NASA.
Resources
- Leia sobre a ‘boa’ e ‘má’ ciência no Armageddon visitando o site Bad Astronomy.
- Para informação sobre asteróides e cometas, visite o muito compreensivo site de Bill Arnett Nine Planets.
- Veja uma palestra TED que explica como poderíamos defender a Terra de asteróides, no TED website.
- O Spaceguard Centre (localizado em Knighton, Powys, Reino Unido) fornece informação sobre a ameaça de impacto de asteróides e cometas e sobre as formas como podemos prevê-lo e negociá-lo. Para mais informação, visite a respetiva página web.
- As Views do Solar System fornecem um catálogo de crateras de impacto terrestres.
- Para outras críticas e explorações de ciência nos filmes, ver os seguintes livros:
- Rogers T (2007) Insultingly Stupid Movie Physics. Naperville, IL, USA: Sourcebooks Hysteria. ISBN: 1402210337
- Perkowitz S (2010) Hollywood Science: Movies, Science, and the End of the World. New York, USA: Columbia University Press. ISBN: 0231142811
- Weiner A (2007) Don’t Try This at Home! The Physics of Hollywood Movies. New York, USA: Kaplan Publishing. ISBN: 1419594060
- Edwards R, Brooks M (2017) Science(ish): The Peculiar Science Behind the Movies. London, UK: Atlantic Books. ISBN: 1786492210
Review
Esta atividade é muito interessante e divertida para os alunos. Que melhor maneira de despertar a curiosidade dos alunos e o seu pensamento crítico? A verificação ou o descrédito de factos derivados de filmes de ficção permite aos alunos gerar as suas próprias questões sobre os mesmos e pensar como essas questões podem ser respondidas aplicando os seus conhecimentos de Física e Matemática. Independentemente de quão surreais algumas cenas dos filmes sejam, haverá sempre um princípio científico que pode ajudar a explicar a sua possibilidade ou impossibilidade.
O uso da ciência para explicar filmes de ficção pode também levar a algumas discussões muito elaboradas quando os alunos pensarem sobre os factos enunciados nos filmes e não apenas tomarem-nos por garantidos. Os alunos podem ser motivados para expandir a sua área de investigação conforme necessário e substanciar os seus argumentos com provas matemáticas. Este exercício pode também alertar os alunos para os factos científicos existentes por todo o lado, tanto na vida real como na ficção.
Catherine Cutajar, professor de Física, St Martin’s College, Malta





