A Geometria pode levar-nos à Lua Teach article
Meça a distância da Terra à Lua com recurso à Geometria do Secundário e a uma rede internacional de escolas e observatórios.

A imagem é cortesia da NASA
Estique o seu braço e, olhando para o seu polegar, observe-o primeiro com um só olho e depois só com o outro. A aparente deslocação do polegar com respeito ao fundo é chamado de paralaxe. O mesmo princípio aplica-se se duas escolas diferentes ‘olharem’ para a Lua: vê-la-ão ligeiramente deslocada com respeito às estrelas de fundo.
Nesta atividade, escolas em continentes diferentes juntam-se de forma a que alunos com idades entre os 16 e os 19 anos comparem as suas observações da Lua feitas a várias distâncias sobre a Terra e calculem a distância da Terra à Lua graças aquelas (figura 1). Equipados com apenas uma boa máquina fotográfica e um bom conhecimento de Geometria, as observações levam, aproximadamente, duas horas e os cálculos cerca de três horas (o estabelecimento das parcerias pode levar um pouco mais de tempo…).
Definindo as condições apropriadas
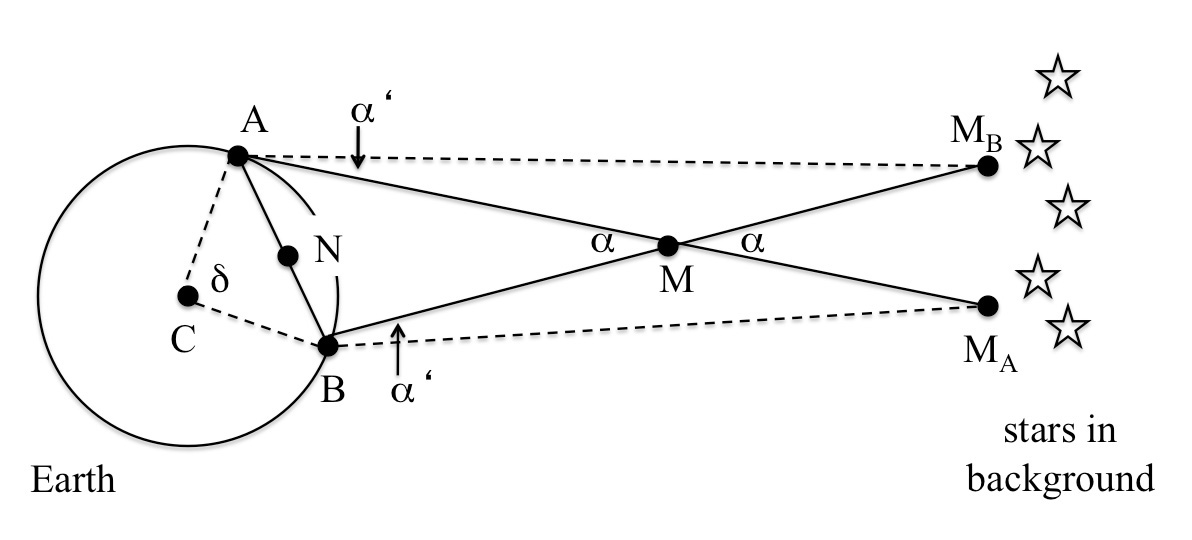
O plano global de observação para a atividade está detalhado na figura 1, onde M é a Lua, representada como um ponto pois o seu tamanho é muito pequeno em relação à distância a calcular (aproximadamente, cem vezes menos).
Como em muitos empreendimentos científicos, o planeamento é a chave. Neste caso, para além de se definirem as condições necessárias para se fazerem as observações, o professor precisa de determinar qual a margem de erro que se aceita: isto é importante de forma aos alunos não ficarem desapontados se não encontrarem a distância exata. Abaixo lista-se um conjunto de pontos importantes a realçar quando se discutir esta atividade com a turma mas também quando se estiver a preparar a parceria com outra escola.
A imagem é cortesia dos autores
A Figura 1 mostra como dois observadores (A e B) verão a Lua (M) em duas posições ligeiramente diferentes no céu. Embora, na realidade, os dois pontos de observação A e B, M e o centro da Terra (C) não estejam no mesmo plano, para simplificar os cálculos e de forma a poder usar apenas trigonometria no plano, assumimos que estão.
A imagem é cortesia de Nicola Graf
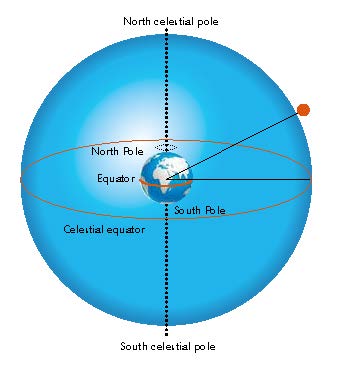
Para que essa aproximação seja o mais exata possível, os dois pontos de observação precisam de estar à mesma longitude e a Lua no seu ponto mais alto (na culminação)w1 aquando da observação. Esta situação ideal é muito difícil de conseguir mas recomendamos que se coloque o mais próximo dela possível e que esteja a par dos erros implicados por desvios significativos daquelas condições.
Além disso, se o ângulo da Lua com o equador celeste (declinação)w1 é igual à média das latitudes de A e B, ABM forma um triângulo isósceles e isto simplifica ainda mais os cálculos.
O céu de fundo ideal
Também vai precisar de, pelo menos, duas estrelas brilhantesw1 (ou planetas) de fundo, de forma a identificar as duas posições aparentes da Lua, MA e MB.
Assunções geométricas
Então, vamos considerar que as duas retas AMA e BMA são quase paralelas, bem como AMB e BMB. Isto quer dizer que temos os ângulos α » α’ (figura 1). Embora não exatamente verdade, esta assunção é aceitável uma vez que os pares de retas convergem longe quer da Terra, quer da Lua. Claro que isto parece muito longe de ser verdade na figura 1, uma vez que esta não está desenhada à escala.
Se medirmos o ângulo α e a distância AB – conhecida como linha-de-base – e um outro ângulo no triângulo ABM, podemos calcular todas as outras distâncias. Caso contrário, podemos fazer com que o triângulo ABM se torne isósceles e o conhecimento de α e AB é suficiente para o cálculo de todas as distâncias.
Um ponto-chave é que a linha-de-base seja longa o suficiente quando comparada com a distância que pretendemos encontrar, de forma a evitar que a paralaxe se torne pequena demais. Para a Lua, uma distância entre as escolas parceiras de cerca de 1000 km é suficiente, mas quanto maior for, melhor.
Mas ainda existirão erros…
Apesar de todo o cuidado a empenhar na escolha das melhores condições, as medições não serão perfeitas. As principais fontes de erro são:
- Imprecisão em visualizar o deslocamento da Lua nas duas imagens, principalmente devido à sobre-exposição do disco lunar;
- A, B, C e M não estarem exatamente num plano;
- Distorções devido às lentes das máquinas fotográficas;
- Condições de observação;
- Refração atmosférica;
- Sincronização temporal.
Os erros devido a 4) e 5) não são muito importantes: a nossa medição é baseada em grandes ângulos e, assim, não é grandemente afetada por uma imprecisão de uns poucos segundos de arco.
A sincronização temporal (6) também não é muito importante pois a Lua viaja o equivalente ao seu próprio diâmetro numa hora, pelo que uma sincronização imperfeita de uns poucos segundos (ou mesmo minutos) não é relevante.
As distorções devidas às lentes de máquinas fotográficas (3) podem-se reduzir se se utilizar um pequeno ângulo de visão, como aquele que é dado por uma teleobjetiva. Uma lente normal de máquina fotográfica introduz um erro maior, mas ainda aceitável. No nosso caso, esse ângulo não era assim tão pequeno e estimamos que gerou uma imprecisão de cerca de 1-2%.
Os erros devido a 1) e 2) são os mais importantes e podem contribuir com uma imprecisão de 5-10% cada um. Em conjunto, são responsáveis por um erro global de cerca de 10-20%. Para reduzir 1) devemos escolher uma longa linha-de-base de forma a que a deslocação da Lua seja a maior possível; para reduzir 2) devemos escolher, apropriadamente, os locais e momentos de observação de forma a que A, B, C e M fiquem no mesmo plano. Se ambas as condições forem respeitadas (para nós a primeira condição foi-o, mas não a segunda) o erro pode-se reduzir a uns poucos por cento.
A rede de paralaxe
Nós montámos uma rede de escolas, observatórios e educadores por todo o planeta de forma a concretizar esta medição. É composta pelos seguintes membros:
- Mario Koch, professor no Friedrich-Schiller-Gymnasium em Weimar, Alemanha
- Noorali Jiwaji, professor de Física na Open University of Tanzania em Dar es Salaam, Tanzânia
- Frank Oßwald, professor no Goethegymnasium em Weissenfels, Alemanha
- Matthias Penselin, professor no Albert Schweitzer Gymnasium Crailsheim e na House of Astronomy em Heidelberg, Alemanha
- Alexander GM Pietrow, IostoFodde and Jelle Mes, estudantes do Leiden Observatory e membros do comitê de observações do Leidsch Astronomisch Dispuut ‘F. Kaiser’, Leiden, Países Baixos
- Elena Servida, professor no Liceo Vittorio Veneto em Milão, Itália
- Brian Sheen, Roseland Observatory, St Austell, Reino Unido
Com esta rede, ou outra que seja sua, os professores podem propor datas para conduzir observações lunares de forma a determinar a distância da Terra à Lua.
As grandes distâncias entre as escolas na nossa rede fornecem uma linha-de-base suficientemente longa (distância AB) para tornar possível medir a distância da Terra a Marte em maio de 2016 (Cenadelli et al, 2009; Penselin et al, 2014). Nessa altura a Terra estará situada entre o Sol e Marte e Marte estará quase à distância mais próxima possível da Terra, uma posição ideal para tais observações.
Se gostaria de contactar qualquer parte desta rede internacional para efetuar medições, por favor contacte Davide Cenadelli em davide.cenadelli@unimi.it
Material
O único material específico necessário é uma boa máquina fotográfica para tirar fotos da Lua e do céu. Uma teleobjetiva com um comprimento focal de cerca de 100-200 mm é a melhor escolha, mas uma lente normal também funcionará se as estrelas brilhantes ou os planetas de fundo não estiverem muito próximos da Lua.
Procedimento
- Use a rede de paralaxe (veja a caixa) para encontrar uma escola ou um observatório que esteja a uma longitude semelhante à da sua escola.
- Anote a latitude e longitude dos dois parceiros (λ = latitude, l = longitude). Aqui usamos observações feitas na Cidade do Cabo, África do Sul, e no Observatório Astronómico da Região Autónoma do Vale de Aosta (OAVdA), Itália:OAVdA, Itália: (λI 45.78° N, lI 7.48°E)
Cidade do Cabo, África do Sul: (λS 33.93° S, lS 18.42° E)
- Combinem as datas e as horas exatas para as observações da Lua (é melhor planear várias datas, caso o tempo esteja mau). Os dois observadores acima concordaram fazer uma observação simultânea no dia 2 de fevereiro de 2015 às 20h02 UT. Nessa noite estavam disponíveis dois corpos brilhantes de referência, Júpiter e Procyon (αCMi) que, no céu, não estavam longe da Lua; aqueles poderiam servir como pontos de referência contra os quais medir a posição da Lua.As melhores circunstâncias são quando planetas ou estrelas brilhantes de fundo, tais como Júpiter e Procyon, são visíveis perto da Lua e, idealmente, tão próximo quanto possível à mesma de forma a que uma teleobjetiva com um pequeno campo de visão possa ser usada. Isto ajuda a evitar a os enormes efeitos de distorção de perspetiva, típicos de lentes grande-angular.
- Na data escolhida, todos os participantes com céu limpo devem registar várias imagens da Lua com uma máquina fotográfica, seguindo a agenda temporal pré-definida. As imagens precisam de mostrar tão claramente quanto possível a Lua e os dois objetos brilhantes de referência. Devem ser captadas com diferentes tempos de exposição, de forma a escolher o melhor compromisso entre uma Lua não demasiadamente brilhante e algumas estrelas de fundo que ainda sejam visíveis.
- Sobreponha as imagens de dois observadores diferentes numa única imagem, como na figura 2.

Sobreposição das duas imagens recolhidas simultaneamente no dia 2 de fevereiro de 2015 às 20h02 UT, por um observador na Cidade do Cabo e outro no OAVdA.
A imagem é cortesia dos autores
- Meça a distância de Júpiter a Procyon numa imagem e mude a escala na outra imagem de forma a que a distância entre esses objetos seja a mesma (mesma escala nas duas imagens);
- Sobreponha as imagens e marque a posição da Lua como vista pelas duas escolas na mesma imagem;
- Meça o desvio do centro da Lua.
- Calcule a linha-de-base da paralaxe, AB, como se mostra na figura 1.O ângulo, δ, entre os dois observadores A e B pode ser calculado como segue (Roy & Clarcke (1977):
cos δ = sin λI sin λS + cos λI cos λS cos(lI − lS )
= −sin (45.78°) sin (33.93°) + cos (45.78°) cos (33.93°) cos (10.94°)
= 0.1681
Assim δ = 80.32° (1)
Se assumirmos que a Terra é perfeitamente esférica e que o seu raio é 6367 km, a linha-de-base AB é dada por:
AB = 2BN
= 2(CB * sin (δ/2))
= 2 × 6367 km × sin (80.32°/2)
= 8212 km (2) - Calcule o ângulo de paralaxe, α.
Simplesmente com o uso de uma régua, podemos estimar que o desvio da Lua que observamos (figura 2) é de cerca de 2.4 diâmetros lunares. Como visto da Terra, o diâmetro lunar subtende um ângulo de 0.5°; ou seja, se desenharmos duas retas do olho de um observador até cada um dos extremos do diâmetro lunar, o ângulo entre as linhas é de 0.5°:
α = 2.4 * 0.5 = 1.2° - Calcule a distância entre a Lua e o centro da Terra, CM.
Vamos calcular CM em duas situações. Em ambas assumimos que A, B, M e C estão no mesmo plano.
Caso 1: ABM é um triângulo isósceles
Neste caso, os ângulos BAM e ABM são iguais e:
CM = CN+NM
= CA cos δ/2 + ([AB/2]/[tan α/2])
= 4866 + 392 080 km
= 396 900 km (3)
A distância conhecida no momento das mediçõesw1 era 397 900 km e, assim, obtivemos um valor que é uma estimativa por defeito por apenas 0.3%. Devido às aproximações usadas esta precisão foi, apenas, pura sorte.
Caso 2: ABM não é um triângulo isósceles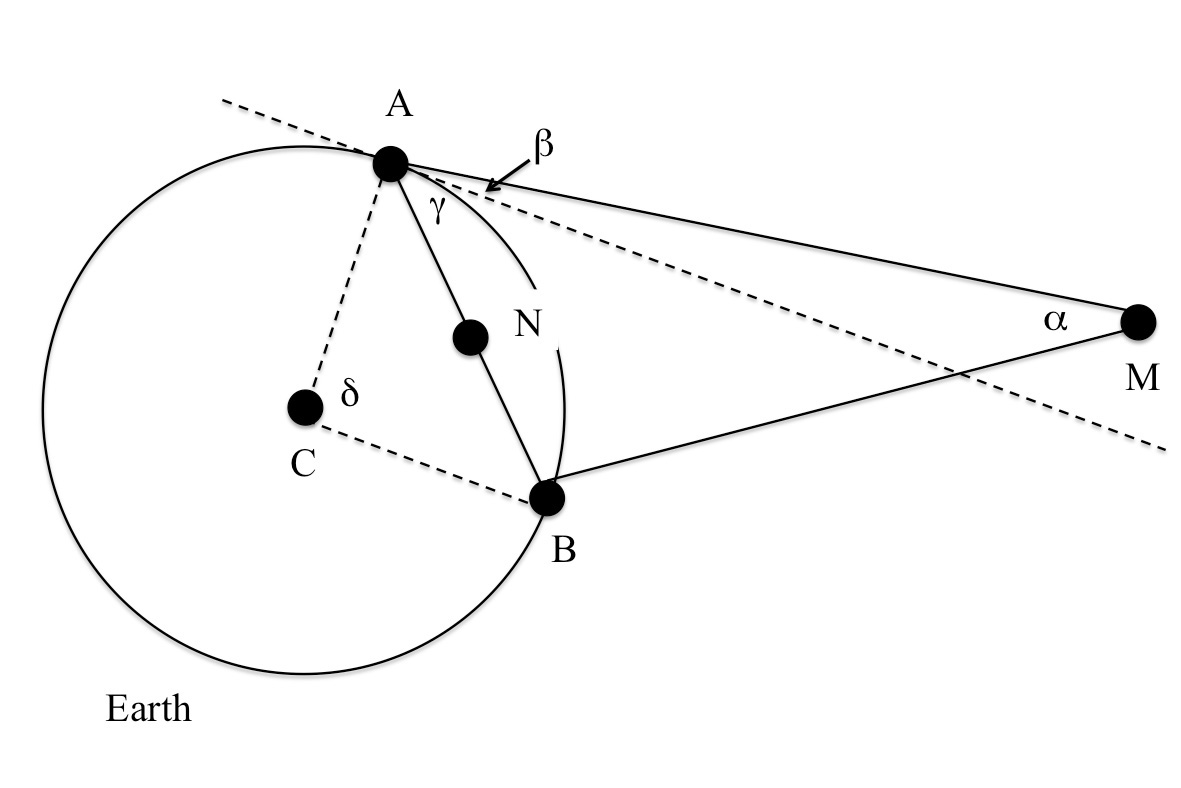
Figura 3: Destaque da secção da figura 1 que mostra o espaço entre a Terra e a Lua e os ângulos β e γ
A imagem é cortesia dos autoresSe deixarmos cair a assunção de que AMB seja um triângulo isósceles, precisamos de saber o valor de outro ângulo, tal como BAM. BAM é igual à soma de β, i.e., a altura da Lua acima do horizonte como vista de A, e γ (veja a figura 3). β pode ser medido com equipamento específico ou, na ausência deste, pode ser tomado como quase idêntico à alturaw1 de uma das estrelas ou planetas de referência que usamos para medir o desvio da Lua. Para Procyon, obtivemos β = 39.3°.
Podemos calcular γ usando o valor de δ que calculamos antes e a regra geométrica diz-nos que: γ = δ/2.
Segue que BAM = β + γ = 79.5°.
Finalmente, se aplicarmos a lei dos senos ao triângulo ANM, temos:
ΝM/sin79.5° = AN/sin(α/2)
ΝM = AN (sin79.5°/sin0.6°)
≈ 385 536 km (4)
e, assim_
CM = CN + NM
= CAcosα/2 + NM
= 4866 + 385 536 km = 390 400 km (5)
Este resultado ainda é realista e apenas 1.9% abaixo do valor conhecido.
Agradecimentos
Os autores gostariam de agradecer encarecidamente a todos os participantes na nossa rede, bem como aos alunos que participaram no ESO Camp 2014 pois fizeram medições semelhantes.
O Observatório Astronómico da Região Autónoma do Vale da Aosta é financiado pelo Governo Regional do Vale de Aosta, pelo município de Nus e pela Comunidade do Monte Emilius. Andrea Bernagozzi desenvolveu parte do trabalho para este projeto enquanto apoiado por uma bolsa da União Europeia – Fundo Social Europeu, da Região Autónoma do Vale da Aosta e do Ministério Italiano do Trabalho e das Políticias Sociais.
References
- Cenadelli D et al. (2009) An international parallax campaign to measure distance to the Moon and Mars. European Journal of Physics 30: 35-46
- Penselin M, Liefke C, Metzendorf M (2014) Zweifacher Blick auf erdnahen Asteroiden. Sterne und Weltraum 11: 72-77
- Roy AE, Clarcke D (1977) Astronomy: Principles and Practice. Bristol, UK: Adam Hilger. ISBN: 0852743467
Web References
- w1 – De forma a encontrar os valores necessários para efetuar os cálculos descritos neste artigo, pode usar o simulador do céu Stellarium, um planetário gratuito e open-source para o seu computador.
Resources
- O método utilizado neste artigo também está descrito em muitos livros de astronomia. Por exemplo, veja:
- Karttunen H et al (2007) Fundamental Astronomy 5th edition. Berlin, Germany: Springer. ISBN: 9783540341437
- O material didático relacionado com Penselin et al (2014), que pode ser utilizado diretamente em sala de aula, encontra-se no sítio web da Wissenschaft in die Schule (apenas em alemão).
Review
Este artigo descreve uma forma simpática de juntar a Matemática a outras áreas científicas, tal como a Física. Mostra como calcular a distância à Lua, ou mesmo Marte, com recurso aos nossos próprios dados obtidos por imagens de máquina fotográfica e da nossa instituição parceira (e.g. rede paralaxe). Com recurso à Matemática Pura – ou Matemática Aplicada Pura, uma vez que se resolve um problema real – é possível obter bons resultados.
Devido à sua curta mas eficiente introdução, este artigo pode ser usado por professores de ciências ou de matemática.
Gerd Vogt, Higher Secondary School for Environment and Economics, Yspertal, Austria





