Galileu e as luas de Júpiter: explorando o céu noturno de 1610 Teach article
Carla Isabel Ribeiro. Aprenda como os seus alunos podem usar a Matemática para estudar as luas de Júpiter.

(Justus Sutermans, 1636)
Imagem do domínio público;
fonte da imagem: Wikimedia
Commons
Numa noite de janeiro de 1610, Galileu Galilei olhou para Júpiter através do seu telescópio e viu o que pensou serem três estrelas próximas do planeta. Ele continuou as suas observações durante cerca de dois meses e apercebeu-se que, de facto, as “estrelas” eram quatro e que estas mudavam de posição em torno de Júpiter. Galileu concluiu que as “estrelas” eram, na realidade, planetas a orbitar Júpiter – os planetas Mediceus como os batizou na altura, mas que agora são conhecidos como luas galelianas em honra do seu descobridor (figura 1).
“… eu deveria revelar ao mundo e publicar a descoberta e observação de quatro PLANETAS nunca antes vistos, desde o início do mundo até aos nossos dias…”
Galileu Galilei Sidereus Nuncius (O Mensageiro das Estrelas; 1610)

galelianas Io, Europa,
Ganímedes e Calisto (Júpiter
não está à mesma escala que
os satélites).
Imagem cortesia de NASA
Planetary Photojournal
Esta descoberta de Galileu é a base de um projeto que concebi para os meus alunos de Física do 12º ano (17-18 anos de idade) quando lecionei o movimento harmónico simples. Este foi construído a partir de uma atividade semelhante que desenvolvi anteriormente, sobre o movimento da lua galeliana Io (Ribeiro, 2012). O atual projeto é baseado no ensino por descoberta orientada e tem como objetivo envolver os alunos numa variedade de processos científicos – desde a exploração de contextos históricos, à obtenção e análise de resultados experimentais, e até à comunicação das suas conclusões a terceiros.
O objetivo do projeto é que os alunos provem que Galileu estava correto quando afirmou que as “estrelas” próximas de Júpiter eram, de facto, satélites do planeta. Para isso, os alunos recolhem dados sobre o movimento das luas usando uma simulação computacional e depois mostram que este movimento tem as características do movimento harmónico simples, com Júpiter no centro do movimento. No final do projeto, os discentes elaboram um relatório (documento ou apresentação) para comunicarem o processo e os resultados obtidos e, idealmente, partilham-nos com estudantes de outros países, aprendendo assim a comunicar um trabalho científico internacionalmente.
A duração do projeto varia, dependendo de como o professor decidir desenvolvê-lo. Eu trabalhei com os meus alunos durante quatro meses, mas se não tiver disponibilidade para desenvolver todo o projeto, pode-se selecionar apenas uma de todas as atividades.
O movimento harmónico simples e o movimento circular uniforme
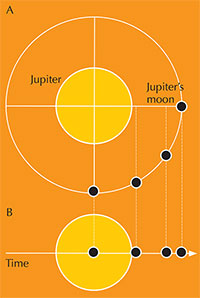
das luas galelianas à volta de
Júpiter: A) como visto acima
do plano da órbita e B) como
visto desde a Terra. Os
pontos representam as
posições ocupadas pela lua
galeliana em intervalos de
tempo iguais. Clique na
imagem para ampliar.
Image courtesy of Carla Isabel
Ribeiro
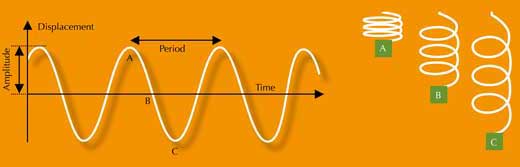
Imagem cortesia de Nicola Graf
O movimento harmónico simples (MHS) é o termo usado para descrever movimentos periódicos regulares como o movimento de um pêndulo ou as oscilações de um objeto preso a uma mola. Traçando o gráfico da elongação em função do tempo destes movimentos obtém-se uma onda sinusoidal (figura 2).
O MHS pode ser interpretado como a projeção num eixo de um objeto que se move com um movimento circular uniforme (MCU). Por exemplo, imagine um objeto movendo-se em círculos num plano horizontal. Se o observarmos lateralmente, ao nível dos olhos (o equivalente à projeção no eixo das abcissas), vemos um movimento para a frente e para trás, como um objeto a oscilar preso a uma mola. Só quando observamos o movimento “de cima”, paralelo ao plano, é que vemos o movimento como circular.
A relação entre o MHS e o MCU pode ser aplicada às luas galelianas como vistas desde a Terra: parecem descrever um MHS, devido à projeção do seu MCU à volta do planeta na nossa linha de visão (figura 3). (As órbitas são ligeiramente excêntricas, mas a excentricidade é tão pequena que se pode considerar que as luas têm uma órbita circular e que se movem a velocidade constante.)
Cosmologia no tempo de Galileu

séc. XVI do modelo
geocêntrico do Cosmos por
Bartolomeu Velho em
Cosmographia (1568). Clique
na imagem para ampliar.
Imagem de domínio público;
fonte: Wikimedia Commons
As observações das luas de Júpiter, por Galileu, foram realizadas num período de transição entre o modelo geocêntrico de Aristóteles e da Igreja Católica, centrado na Terra (figura 4), e o modelo heliocêntrico, centrado no Sol.
Obviamente, Galileu adotou explicitamente o modelo heliocêntrico alguns anos mais tarde, em desafio à doutrina católica. No entanto, as suas observações realizadas com o telescópio e publicadas no seu livro Sidereus Nuncius (O Mensageiro das Estrelas) em 1610, já causavam atritos por contradizer os ensinamentos de Aristóteles. No modelo aristotélico, tudo no Cosmos orbitava a Terra, por isso a ideia de luas a orbitarem Júpiter estava em contradição com este modelo.
O projeto etapa a etapa
Etapa 1: o modelo cosmológico no séc. XVII
Peça aos alunos que pesquisem os modelos cosmológicos aceites na Europa do início do séc. XVII. Que efeitos terão tido nas investigações e conclusões de Galileu? Os alunos também deverão ler excertos do O Mensageiro das Estrelasw1, no qual Galileu descreve as suas observações e conclusões.
Etapa 2: escolher o software de planetário
Terá que descarregar o programa de planetário gratuito Stellariumw2 ou outro similar. Depois, divida os alunos em quatro grupos e atribua, a cada um, uma das quatro luas galelianas (Io, Calisto, Ganímedes ou Europa).
Etapa 3: seguir as luas de Júpiter

Peça aos alunos que usem o programa Stellarium para determinarem a posição da lua ao longo do tempo: numa tabela, o grupo deverá registar a elongação (x) – a distância entre a lua e o centro de Júpiter – em diferentes instantes (t). Também deverão medir a amplitude (A) ou seja, a distância máxima da lua ao centro do planeta.
As medições para cada uma das luas deverão ser feitas em intervalos diferentes, dependendo da distância a que estão de Júpiter e, consequentemente, do seu período orbital. Os alunos deverão descobrir o intervalo mais adequado para cada lua por tentativa e erro. A finalidade é obter, pelo menos, 10 medições em que uma delas deverá ser o valor de A.

Por exemplo, Io é a lua mais próxima de Júpiter, o que significa que tem o menor período de translação. Se os alunos optarem por intervalos de 1h, as medições obtidas não serão suficientes; intervalos de 15 minutos serão mais apropriados. Para uma das luas galelianas mais afastadas, usar intervalos de 15 minutos resulta em mais dados do que aqueles que serão necessários, por isso deverão ser utilizados intervalos de tempo maiores.
Para encontrar o centro do planeta nas imagens do Stellarium, os alunos podem usar as marcas vermelhas à volta de Júpiter (figura 5) para traçarem duas linhas que cruzam no seu centro. Para medir a distância entre esse ponto e a lua em estudo podem usar um programa de imagem ou imprimir as imagens e medir as distâncias com uma régua.

freeware programme
Stellarium of Jupiter and its
moons Europa (A) and Io (B).
Click on images to enlarge.
Images courtesy of Stellarium
Etapa 4: teste às conclusões de Galileu
A quarta etapa, e também a mais complexa para os alunos, consiste em mostrar que Galileu estava correto quando concluiu que o MHS que observou era devido a um MCU da lua à volta do planeta.
Para determinar o período orbital, T , da lua em estudo os alunos necessitam da equação matemática do MHS:
x = A × sin(ω t + φ) (1)
em que ω é a frequência angular e φ é uma constante (a constante de fase), e da equação que relaciona ω and T:
ω = 2π / T
em que x é a elongação, A é a amplitude ou a elongação máxima, t é o tempo e φ é uma constante (a constante de fase).
A equação (1) pode ser transformada na equação linear (2):
x = A × sin(ω t + φ) (1)
→ x / A = sin(ω t + φ)
→ arcsin(x / A) = ω t + φ
Cosmo ω = 2π / T
→ arcsin(x / A) = (2π/ T)t + φ (2)
Se os alunos observarem um objeto com o comportamento descrito pela equação (2) – do MHS – então é razoável concluir que este orbita o planeta como uma lua.
Porque a equação (2) é linear, os alunos podem usar os dados recolhidos na etapa 3 para traçar o gráfico arcsin(x / A) em função de t, e o declive do gráfico será 2π / T, a partir do qual os alunos facilmente calculam o período orbital T. A constante de fase da lua, φ, é a ordenada na origem. A figura 6 mostra um exemplo de um gráfico que os alunos podem traçar usando os dados para a lua Europa.
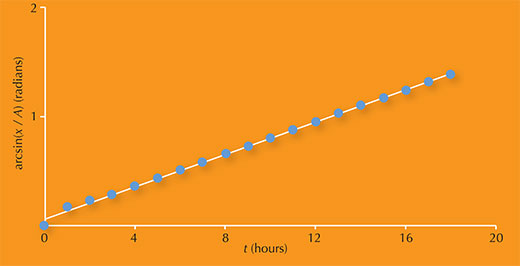
Imagem cortesia de Carla Isabel Ribeiro
O gráfico tem um declive de 0,0741.
Como o declive é igual a 2π / T, então:
2π / T = 0.0741
→ T = 2π / 0.0741
= 84.8 h
Os alunos com conhecimentos matemáticos mais avançados podem fazer uma análise de regressão linear para testar a adequação da reta da equação (2) aos dados experimentais. O valor obtido no caso de Europa (R2 = 0,998) mostra que os dados se ajustam à equação e assim confirmam que o objeto se comporta como uma lua em órbita.
O valor aceite para o período orbital de Europa é cerca de 3,55 dias (85,2 h), que é aproximado ao valor calculado. A diferença entre estes dois valores pode ser o ponto de partida para uma discussão sobre a exatidão dos resultados experimentais. O que poderá ter corrido mal? Os erros foram aleatórios ou sistemáticos?
Neste caso, o erro deverá ter tido a sua origem na medição de A, pois as posições da lua foram simuladas com o intervalo de 1h e a elongação máxima pode ter sido atingida entre duas medições. Pode perguntar aos alunos sugestões para minimizar este erro.

Duque de Veneza como usar
o telescópio (HJ Detouche,
1754). Clique na imagem
para ampliar.
Imagem do domínio público;
fonte da imagem: Wikimedia
Commons
Etapa 5: apresentação dos resultados
A última etapa para cada um dos grupos é que estes apresentem o seu trabalho, com a descrição de toda a investigação e os resultados obtidos. Em ciência, é importante comunicar a investigação que se faz, por isso os alunos podem mostrar as suas apresentações a alunos de outras turmas ou nos dias abertos ou feiras da escola. Eles deverão pensar na melhor maneira de transmitir o seu trabalho. Como poderão tornar a apresentação simples para que os outros entendam o trabalho? Que imagens poderão usar para explicar o que fizeram?
Poderão ser mais ambiciosos e estabelecerem uma colaboração com uma escola de outro país. Os cientistas por vezes têm que comunicar em língua estrangeira – frequentemente, mas nem sempre – em inglês. Com este projeto espero estabelecer uma colaboração internacional através da rede eTwinningw3. Eu também gostaria de ter notícias de outras escolas que gostariam de trabalhar em conjunto neste projeto.
References
- Ribeiro CI (2012) Io and its simple harmonic motion. Physics Education 47: 268-270. doi: 10.1088/0031-9120/47/3/F04
Web References
- w1 – Pode descarregar uma recente tradução inglesa do Sidereus Nuncius Sidereus Nuncius (O Mensageiro das Estrelas), o famoso trabalho de Galileu onde este descreve as suas descobertas feitas com o telescópio. As páginas 17 e 18 contêm as suas observações das luas de Júpiter para as datas referidas neste projeto.
-
A edição original também está disponível online.
-
- w2 – Stellarium, o programa de simulação de um planetário usado neste projeto pode ser descarregado gratuitamente.
- w3 – O website eTwinning promove a colaboração entre escolas europeias através do uso das técnicas de informação e comunicação (TIC). Disponível em 23línguas, tem quase 50.000 membros e mais de 4.000 projetos registados entre duas ou mais escolas em toda a Europa.
Resources
- O sítio The Physclips mostra uma explicação do movimento harmónico simples, com vídeo e animação.
- O sítio NASA’s Solar System Exploration tem informações atuais sobre Júpiter e as suas luas, incluindo missões espaciais.
- Para um artigo que descreve um projeto similar que explora as luas galelianas usando um telescópio equipado com uma câmara CCD ver:
-
de Moraes IG, Pereira JAM (2009) Using simple harmonic motion to follow the Galilean moons – testing Kepler’s third law on a small system. Physics Education 44: 241. doi: 10.1088/0031-9120/44/3/002
-
O artigo pode ser descarregado gratuitamente a partir do sítio da Universidade de Picardie, França.
-
- O projeto CLEA (Contemporary Laboratory Experiences in Astronomy), do Gettysburg College, EUA, disponibiliza exercícios laboratoriais que ilustram técnicas modernas de Astronomia. Cada exercício consiste num programa de computador, num manual do aluno e um guia técnico para o professor. Vários destes exercícios envolvem as luas de Júpiter.
Review
Este artigo sugere uma nova maneira de ensinar, por descoberta orientada, o movimento harmónico simples: os alunos usam os seus conhecimentos matemáticos, físicos e de TIC para caracterizar o movimento das luas de Júpiter. Eles recolhem os dados a partir de um programa de computador, processam-nos e depois constroem gráficos, particularmente de funções seno e arco-seno, para calcular os períodos orbitais das luas.
A natureza interdisciplinar do artigo serve para tornar a ciência mais agradável. Assim, a atividade desenvolve algumas capacidades como apresentação de resultados e sua comunicação. Ao aderir a uma projeto internacional, os alunos teriam a oportunidade para partilharem os seus resultados, não só com elementos da turma, mas também com alunos de outros países.
Corina Toma, Escola Secundária de Ciências Computacionais “Tiberiu Popoviciu” Cluj Napoca, Romania





