Supporting materials
Déclarations de témoins (Word)
Download
Download this article as a PDF

Comment utiliser les lois physiques pour comprendre ce qui arrive dans une collision avec une voiture, et en tirer parti.

Les élèves qui habitent dans des zones rurales d’Ecosse, apprennent à conduire à la ferme, et croient savoir le faire dans le trafic. Cela a hélas produit de nombreux accidents mortels. Pour réagir à ces événements choquants, nous avons créé une activité scolaire pour que les élèves prennent conscience des dangers que leur conduite crée sur eux-mêmes, sur les autres conducteurs et sur les piétons. Cette activité montre aux élèves une application concrète des lois physiques.

Dans cette activité, nous avons reconstitué une collision réelle qui s’est produite entre une voiture et un piéton de notre région, lequel ne s’en est jamais remis. On ignore les circonstances exactes de cet accident, car le chauffeur a disparu après le collision, et il n’y avait pas de témoin direct. Les élèves ont essayé de reconstituer l’accident en utilisant les mesures tirées du rapport de police. Leur but était de découvrir la cause de l’accident, son auteur et si la voiture était en excès de vitesse.
Bien que les élèves auraient préféré se rendre sur place pour faire leurs propres mesures, on peut néanmoins leur donner celles faites par les enquêteurs, comme la longueur de la trace de freinage. Cela leur donne une excellente occasion d’appliquer les équations du mouvement dans le concret.
Cette activité peut être faite par des élèves de 13 à 17 ans, selon leurs connaissances en mathématiques. Les calculs sont faits en fonction des limitations de vitesse en usage au Royaume Uni. Mais il est possible d’inventer d’autres scenarios propres à votre région, et peut-être même d’obtenir des mesures faites par la police locale.
Nous avons demandé aux élèves d’utiliser le scénario suivant pour décrire la scène :
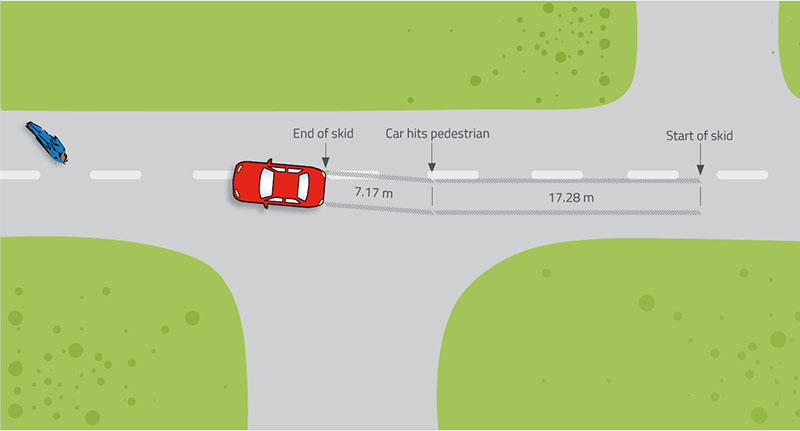
Un piéton est heurté dans une rue tranquille, un soir de pluie vers 22:20, dans une zone où la vitesse est limitée à 48 km/h (30 miles/h). Le piéton est tombé inanimé sur le sol et le conducteur a pris la fuite. Il y avait des témoins assis dans un pub non loin de là. Mais leurs témoignages étaient contradictoires. L’un disati que le piéton était ivre, et l’autre que le conducteur roulait trop vite
Reconstruire une scène d’accident peut durer jusqu’à six heures
Suppléments facultatifs
Cette partie de l’activité prendra deux heures, voire plus, avec le prolongement proposé.
Assurez-vous que les élèves ont lu le témoignange d’un témoin qui pense que le conducteur roulait trop vite.

Pour faire les calculs, les élèves doivent connaître la vitesse de decélération roues bloquées. Des essais analogues ont été effectués par la police avec une voiture semblable, pourvue d’un accéléromètre. On a poursuivi les essais jusqu’à obtenir deux valeurs égales à moins de 10% l’une de l’autre. On choisira la valeur inférieure pour les calculs suivants, afin de mettre le conducteur au bénéfice du doute.
Le résultat de ces mesures montre que la décéleration varie entre les limites :
Les mesures faites permettent de répondre à toutes les questions posées plus bas. Ces mesures correspondent à notre propre simulation. Le lecteur en obtiendra peut-être d’autres.
Queston 1 : Quelle était la vitesse de la voiture au début du dérapage ?
Pour calculer la vitesse de la voiture, on utilise l’équation :
v² = u² + 2as
où :
v = vitesse finale = 0 m s-1
u = vitesse initiale = ?
a = accélération = –6.80 m s–2 valeur inférieure des mesures de la police)
s = déplacement (longueur totale de la trace de freinage, mesurée 24.45 m)
En utilisant l’équation:
0 = u² + (2 x –6.8 x 24.45)
u² = 332.52
Donc u = 18.2 m s–1, ou 65.6 km/h soit beaucoup plus que la limite autorisée.
Question 2 : Quelle était la vitesse de la voiture au moment du choc avec le piéton ?
Pour répondre à cette question, on utilise la même équation :
v² = u² + 2as
où
v = vitesse finale = 0 m s–1
u = vitesse initiale = ?
a = accélération = –6.80 m s–2 (valeur inférieure des tests de la police)
s = déplacement (longueur de la trace après la choc avec le piéton, mesurée 7.17 m)
En utilisant l’équation :
0 = u² + (2 x –6.80 x 7.17)
u² = 97.512 m s–1
Donc u = 9.87 m s–1, donc 35.5 km/h

Question 3: Si la voiture avait respecté la limite de vitesse en ville, est-ce que la collision aurait eu lieu ?
On utilise encore une fois la même équation
v² = u² + 2as
u = vitesse initiale autorisée = 13.41 m s–1 ( ce qui correspond à 30 miles par heure)
0 = 13.41² + (2 x –6.80 x s)
13.41² = 13.60 x s
Ainsi : s = 179.86/13.60
= 13.22 m
Par conséquent, si la voiture avait respecté la vitesse limite de 30 miles par heure, elle se serait arrêtée à environ 4 m devant le piéton, et la collision n’aurait pas eu lieu.
On arriverait à la même conclusion si on avait utilisé la limite de 50 km/h, en usage en Europe
50 km/h = 13.89 m s–1
0 = 13.89² + (2 x –6.80 x s)
13.89² = 13.60 x s
So s = 192.91/13.60
= 14.19 m
Ici encore, la voiture aurait stoppé à environ 3 m devant le piéton, et ne l’aurait pas touché.

A la suite de ces calculs, les élèves devraient pouvoir conclure que la voiture était en excès de vitesse, et que le conducteur était fautif. Dans ce cas réél, le conducteur a été condamné pour conduite dangereuse, puis emprisonné huit mois et puni d’une interdiction de conduire pendant 4 ans, pour avoir causé l’accident et s’être enfui ensuite.
Nous avons trouvé que les élèves impliqués dans cette activité savaient observer, faire des hypothèses, tirer des conclusions et en évaluer la valeur. Cela a également convaincu certains que la physique a une utilité pratique. Nous pensons même que ce genre de leçons permet de justifier comment se fixent les limites de vitesse autorisées en ville.
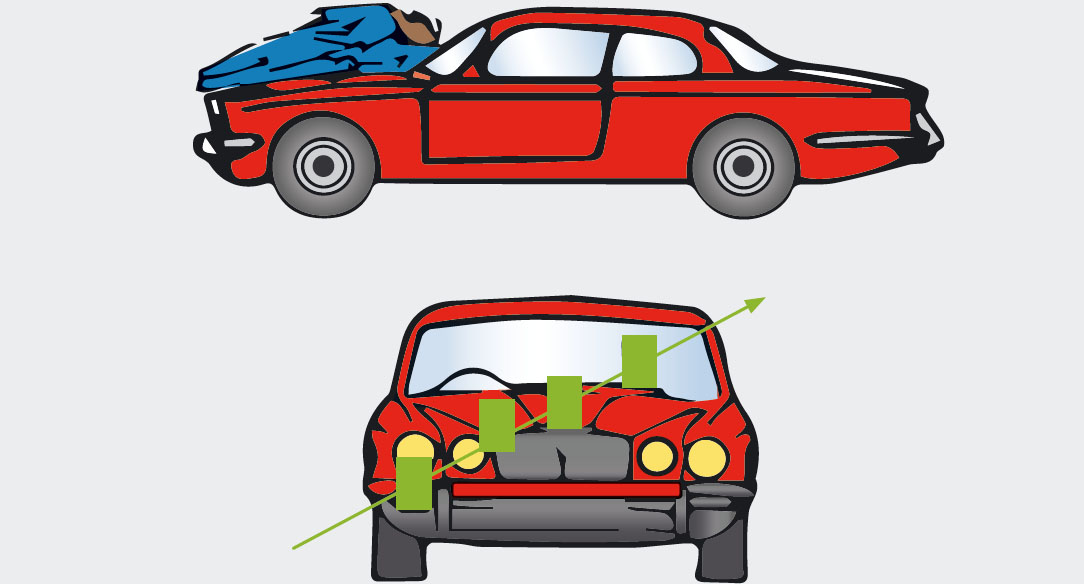
On peut étendre cette etude en examinant ce qui est arrive au piéton après le choc. On peut utiliser des bandes de papier de couleur pour illustrer comment le piéton a été touché puis projeté lors de la collision. Voir la figure 2, où on utilise différentes couleurs pour la voiture et pour les habits du piéton.
La matériel additionnel décrit ci-dessous fournit des informations supplémentaires sur les collisions entre voitures et piétons. Certains détails particulièrement choquants devraient inciter les élèves à la prudence en conduisant.
L’auteur voudrait remercier tous ceux qui ont permis de réaliser ce projet.:
Malheureusement, les accidents de la route sont devenus une banalité dans notre monde. Qu’y a-t-il de mieux que la science pour réduire le nombre de ces accidents, et engager les jeunes à la prudence ?
Cette activité peut être effectuée par des élèves d’âge très différents, et peut être adaptée aux limites de vitesse en vigueur dans d’autres pays. En étudiant un véritable accident de voiture, les élèves sont en mesure d’appliquer les lois de la physique pour comprendre ce qui s’est passé. Ils voient aussi ce qu’est une distance de freinage, et comment elle est affectée par la fatigue, la distraction et l’abus d’alcool ou de drogues, sans parler de l’état de la route, de la météo et de l’usure des pneus. L’ignorance de ces faits peut avoir des conséquences fatales.
Catherine Cutajar, maître de physique, St. Martin’s College Sixth Form, Malte.