Mediciones inteligentes de los cielos Teach article

Traducción de Elisa López Schiaffino. Los estudiantes pueden usar un teléfono inteligente para hacer experiencias prácticas de astronomía.

¿Dónde te encuentras exactamente en este momento? Una manera de saberlo es a través de la función de posicionamiento por satélite de los teléfonos móviles (conocida como GPS). Antiguamente, en cambio, se recurría a las estrellas para saber la ubicación, especialmente los navegantes de mar frente a un paisaje mayormente monótono.

En este artículo, describimos algunos de los primeros avances en la navegación basada en las estrellas, y mostramos cómo reproducir estas técnicas tradicionales en el aula mediante el uso de aplicaciones simples en un teléfono inteligente. Luego los estudiantes pueden usar la función GPS de sus teléfonos para constatar la exactitud de su trabajo y examinar las potenciales fuentes de error.

Ambas actividades son apropiadas para estudiantes de entre 14 y 18 años e incluyen conceptos de historia, astronomía, geografía y matemática: cómo determinar la latitud (figura 1) mediante la altura el Sol, y cómo determinar la latitud mediante la altura de Polaris. En la sección de materiales adicionales puedes descargar detalles de la actividad colaborativa entre distintas escuelas para calcular la circunferencia de la Tierra. Las tres actividades requieren poco más que un teléfono inteligente y no más de una hora cada una.

Cómo determinar la latitud mediante la altura del Sol

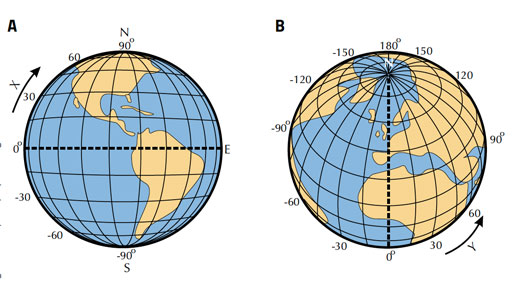
La pregunta “¿Qué es el mediodía?” puede parecer extraña. ¿El mediodía es a las 12 en la mitad del día? En realidad, el mediodía solar es cuando el Sol cruza el meridiano del observador, o línea de longitud, y generalmente parece que el Sol está ubicado hacia el norte o hacia el sur.  Esto ocurre cuando el Sol está en su punto más alto en el cielo y las sombras son lo más pequeñas posibles. En este momento, la posición del Sol puede usarse para determinar la latitud, o distancia angular del ecuador.

¿Cómo se explica esto? Analicemos la situación en uno de los equinoccios (alrededor del 20 de marzo y el 23 de septiembre de cada año), cuando el plano del ecuador pasa por el centro del Sol (figura 2).

• A: Imagina que estás parado sobre el ecuador (latitud 0°) al mediodía: el Sol está justo encima de tu cabeza. Si mides la altura del Sol (su ángulo de elevación sobre el horizonte), verás que es de 90° (figura 3A). Si a este número le restamos 90°, obtendremos como resultado 0°, que es tu latitud.

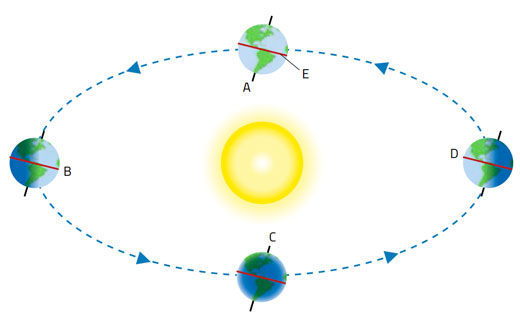
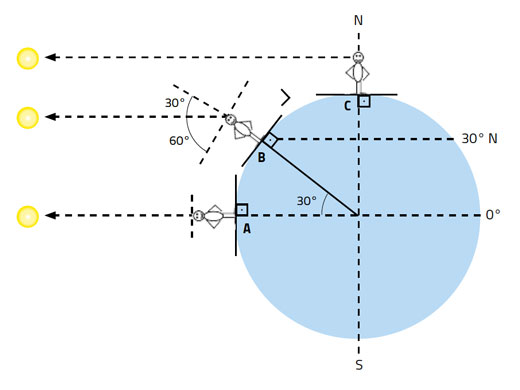
(Hemos indicado que, al mediodía, el Sol generalmente está hacia el norte o hacia el sur. En los equinoccios, está justo arriba).

• B: Una amiga tuya está en el Polo Norte o en el Polo Sur (latitud 90° N o 90° S, respectivamente). En ese mismo momento, ella observaría que el Sol está directamente sobre el horizonte: a una altura de 0° (figura 3B). Si calculamos 90° menos ese número (0°) obtendremos como resultado 90°, que es la latitud de tu amiga.
• C: Otro amigo está en el mismo meridiano que tú, pero a una latitud de 30° N. Debido a que está en el mismo meridiano, también es el mediodía para él, pero observaría el Sol a una altura de 60° sobre el horizonte (figura 3C). Si calculamos 90° menos ese número (60°) obtendremos como resultado 30°, que es la latitud de tu amigo.

Latitud = 90° – altura del Sol al mediodía en el equinoccio    (Ecuación 1)

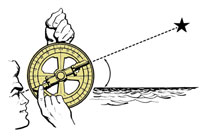
¿Cómo podemos usar este conocimiento en la práctica? En el siglo XV y a comienzos del siglo XVI, muchos navegantes usaban el astrolabio para medir la altura del Sol y así calcular la latitud de la nave. El astrolabio era en esencia un inclinómetro: suspendido en el plano vertical, se lo apuntaba a un cuerpo celeste, por ejemplo el Sol. Se usaba una alidada giratoria para leer la altura del cuerpo celeste de la escala en la circunferencia exterior del anillo (figura 4).

Aunque construir un astrolabio es relativamente sencillo^w2, también resulta fácil usar un teléfono inteligente para medir la altura del Sol con la ayuda de una aplicación con inclinómetro. Sin embargo, antes de proceder debemos realizar un ajuste para que nuestros cálculos funcionen todo el año.

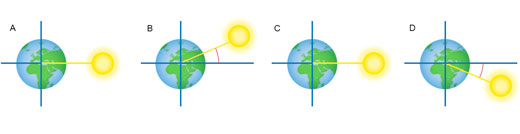
Debido a la inclinación del eje de rotación de la Tierra (23,45°) y a que la Tierra gira alrededor del Sol, el Sol está justo sobre el ecuador solamente en los equinoccios. En el equinoccio de marzo, la posición del Sol al mediodía parece moverse hacia el norte del ecuador, alcanza un ángulo máximo de +23,45° en el solsticio de junio, vuelve a 0° en el equinoccio de septiembre, y se mueve hacia el sur del ecuador hasta alcanzar ‑23,45° en el solsticio de diciembre. Este ángulo es conocido como declinación solar (figura 5).

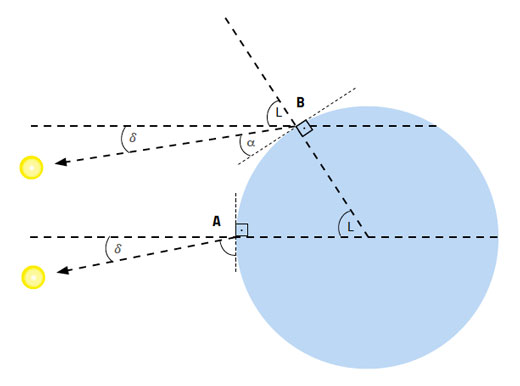
Entonces, la altura del Sol del mediodía, que los primeros navegantes medían con el astrolabio y que ahora podemos medir con un teléfono inteligente, depende de la época del año (o sea de la declinación solar) y de nuestra latitud (figura 6):

Altura del Sol al mediodía = 90° + declinación – latitud           (Ecuación 2)

Or, rearranged:

Latitud = 90° – altura del Sol al mediodía + declinación                         (Ecuación 3)

Para determinar la declinación solar, los navegantes solían usar tablas de datos o sofisticados astrolabios con la declinación solar marcada en el disco giratorio. Podemos obtener la misma información mediante una aplicación de planetario, que nos permite medir la elevación del Sol para determinar nuestra latitud.

Materiales

Cada grupo de estudiantes necesitará:

• Un teléfono inteligente al que se le ha instalado una aplicación de inclinómetro y una de planetario.
• Pajilla para beber
• Cinta adhesiva
• Nivel de burbuja (opcional)

Procedimiento

Para determinar la latitud, los estudiantes deberán:

1. Usar la cinta adhesiva para sujetar la pajilla a uno de los lados del teléfono inteligente (figura 7). Esto es la alidada.
2. Usar la aplicación del planetario para determinar la hora local del mediodía solar y la declinación solar.

De acuerdo a tu ubicación dentro de una zona horaria, el mediodía solar puede estar entre las 11.30 a. m. y la 1.30 p. m., debido al cambio de hora en el verano.

3. Sostener el teléfono con la pajilla sobre el borde superior y apuntar la pajilla hacia el Sol. Cuando la sombra de la pajilla sea lo más pequeña posible, el teléfono estará correctamente alineado (figura 7).
4. Usar la aplicación de inclinómetro y obtener el ángulo de elevación del Sol.
5. Usar la ecuación 2 para estimar la latitud.

Como alternativa, para que los estudiantes puedan apuntar el teléfono hacia el Sol con más precisión y medir la elevación del Sol con más exactitud, podrían construir un soporte que pueda colocarse en un trípode. Los detalles sobre los materiales necesarios y la construcción están disponibles en línea^w3.

Discusión

Pide a los estudiantes que comparen sus resultados con la latitud exacta que obtuvieron con la función GPS de sus teléfonos o con la aplicación de planetario. ¿Qué tan exacto fue el valor calculado? ¿Qué fuentes de error pueden encontrar?

Desde luego, la exactitud dependerá de la precisión del trabajo de los estudiantes, por ejemplo de si la pajilla estaba perfectamente alineada con el borde del teléfono o de si la sombra era realmente la más pequeña posible. Para mayor exactitud, las mediciones deben tomarse al mediodía, pero unos minutos antes o después no afectarán demasiado el cálculo, porque cuando el Sol está en su punto más alto, su altura cambia más lentamente.

Los teléfonos inteligentes pueden medir ángulos de inclinación con una precisión de 0,1°, lo que no está nada mal. Sin embargo, sería interesante calibrar la aplicación de inclinómetro con un nivel de burbuja para saber si la medición de 0,0° es verdaderamente horizontal.

También podría preguntar a sus estudiantes por qué les parece que aunque se podía determinar la latitud en la antigüedad, recién fue posible medir la longitud en el siglo XVIII.

La respuesta se halla en la rotación de la Tierra: 360° por día, o alrededor de 15° por hora. Entonces, si se compara la hora local con la hora de un punto de referencia de longitud conocida, es posible determinar nuestra longitud. Antiguamente podían estimar la hora local con el Sol, pero era difícil medir la hora del punto de referencia: John Harrison inventó un reloj preciso, que incluso podía medir la hora a bordo de una nave en movimiento, recién en 1759.

Cómo determinar la latitud mediante la altura de Polaris

En la actividad anterior, medimos la altura del Sol al mediodía local: cuando el Sol cruza el meridiano del observador. En este momento, y solo en este momento, el Sol parece estar hacia el sur o hacia el norte. Si los estudiantes calcularan la latitud mediante el Sol a otras horas del día, los resultados podrían ser poco exactos. Afortunadamente, hay otro método que no depende tanto de la hora sino de Polaris, la Estrella del Norte, aunque solo funciona en el hemisferio norte y debe realizarse después del anochecer.

Mientras que la posición de otras estrellas parece cambiar durante la noche, Polaris parece permanecer fija en el norte (figura 8), porque su posición está alineada con el eje de rotación de la Tierra. Si te ubicaras en el Polo Norte (latitud 90° N), Polaris parecería estar exactamente arriba, a una altura de 90°. En cambio, en el ecuador (latitud 0°) Polaris parecería estar en el horizonte, a una altura de 0°. Entonces, la altura de Polaris es igual a la latitud del observador: si estuvieras en París, a una latitud de alrededor de 49° N, la altura de Polaris sería alrededor de 49°.

Latitud = altura de Polaris                                 (Ecuación 4)

Los primeros navegantes solían usar un astrolabio para navegar guiados por las estrellas, tal como hacían cuando navegaban guiados por las mediciones solares. En este caso también podemos usar un teléfono inteligente.

Materiales

• Un teléfono inteligente al que se le ha instalado una aplicación de inclinómetro y una de planetario
• Binoculares (opcional)
• Linterna (opcional)

Procedimiento

Calcular la latitud mediante Polaris es más sencillo que hacerlo mediante el Sol: no hace falta tener en cuenta la declinación solar, porque la posición de Polaris permanece igual todo el año.

¿Cómo puedes encontrar a Polaris? Busca la constelación de la Osa Mayor, también conocida como el Carro Mayor (figura 9). Desde las dos estrellas más alejadas del tetrágono, extiende una línea imaginaria hacia arriba y prolóngala aproximadamente siete veces la distancia entre ellas. La primera estrella brillante sobre esa línea es Polaris, que forma parte de la constelación de la Osa Menor. Como alternativa, puedes usar la aplicación de planetario y su función de búsqueda.

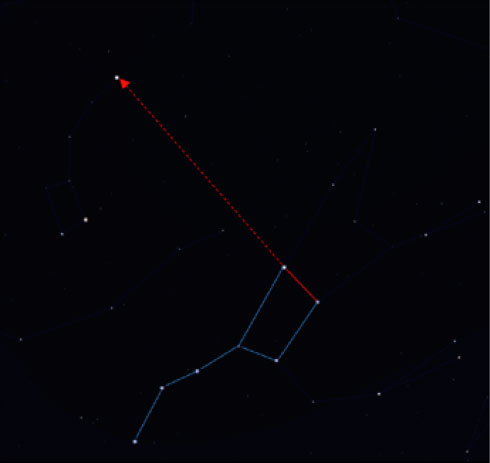
Debido a que Polaris es mucho menos brillante que el Sol, se la puede observar directamente, sin una alidada, pero su tenuidad la hace algo difícil de ubicar. Puedes adquirir habilidad para la medición si practicas con objetos más brillantes, como los planetas o la Luna.

Pide a tus estudiantes que:

1. Sostengan el teléfono con el lado más largo hacia arriba, lo apunten directamente hacia Polaris y miren el frente del teléfono.

Van a precisar algo de luz ambiente para distinguir los bordes del teléfono en la oscuridad.

2. Con la aplicación de inclinómetro, lean el ángulo de elevación de Polaris. Este es el cálculo estimado de la latitud.

Como alternativa, pueden trabajar en pares y usar binoculares. Un estudiante debe apuntar los binoculares a Polaris para que la estrella esté en el centro del campo visual (para que se mantengan estables, pueden apoyar los binoculares, por ejemplo en una pared). Otro estudiante debe apoyar el teléfono sobre los binoculares y determinar el ángulo de elevación con la aplicación de inclinómetro. De ser necesario, calibren los binoculares: ubíquenlos en una superficie horizontal, coloquen el teléfono arriba de los binoculares, y corroboren el ángulo con la aplicación de inclinómetro.

Discusión

Pide a los estudiantes que busquen la altura de Polaris con la aplicación de planetario. ¿Qué tan precisa fue la medición que hicieron? ¿Cómo resultó la latitud estimada comparada con la latitud exacta de la aplicación de planetario o la función de GPS del teléfono? ¿Qué fuentes de error pueden encontrar, además de las que discutieron en la actividad anterior?

Aunque Polaris es una estrella brillante, es considerablemente más tenue que el Sol, por lo que es más difícil obtener una medición precisa de su altura.

Otra fuente de error es la posición de Polaris. Dijimos que Polaris estaría justo arriba si uno estuviera parado en el Polo Norte: a una elevación de 90°. En realidad, la elevación es de 89,3°, lo que incorpora un error de 0,7° en los cálculos de los estudiantes, equivalente a aproximadamente 100 km.

Este método funciona mejor a latitudes medias. Si uno se encuentra muy al norte, es difícil apuntar a la estrella, que está encima de tu cabeza. Cerca del ecuador, Polaris está cerca del horizonte, pero hay turbulencia producida por la atmósfera.

Agradecimientos

Este artículo está basado en una actividad publicada por Science on Stage, una red para docentes europeos de ciencia, tecnología, ingeniería y matemática (CTIM), lanzada inicialmente en 1999 por EIROforum, el grupo de organizaciones que publica Science in School.  Science on Stage reúne a los docentes europeos para que intercambien ideas y prácticas docentes con colegas entusiastas de 25 países.

En talleres de Science on Stage en Viena, Austria y Berlín (Alemania), y también en charlas por correo electrónico y Moodle (una plataforma de aprendizaje de código abierto), 20 docentes de 14 países europeos trabajaron juntos para desarrollar 11 unidades de enseñanza que muestran cómo se pueden usar los teléfonos inteligentes y las aplicaciones para las clases de matemática, física, química y biología. En 2014 Science On Stage de Alemania publicó estas unidades bajo el nombre iStage 2: Smartphones in Science Teaching^w4 (Los teléfonos inteligentes en la enseñanza de la ciencia). Este proyecto cuenta con el apoyo de SAP.

El desarrollo de este proyecto contó con la colaboración de Gerhard Rath y Philippe Jeanjacquot, y también de Pere Compte de España e Immacolata Ercolino de Italia. Martin Pratl brindó ayuda imprescindible con el texto del artículo.