Fonaments a l’aula: mesura de la constant de Planck Teach article
Traduït per Josep Lluís Pau Roigé. Portar el descobriment a l’aula i mostrar als estudiants com calcular la constant de Planck fent servir un equip senzill.

Akimbomidget/Wikimedia
Quan pensem en el càlcul de les constants físiques fonamentals, com ara la velocitat de la llum o la intensitat de la gravetat, probablement pensem en famosos experiments a gran escala, però també es pot fer servir material habitual a les aules per calcular aquestes constants.
La constant de Planck pot semblar un concepte més aviat rar a diferència de, per exemple, la velocitat de la llum, però té un paper absolutament central en la comprensió del comportament de la matèria a nivell subatòmic. És una pedra angular de la teoria de la mecànica quàntica, que descriu l’estrany comportament de les partícules en aquest nivell. Aquí l’energia, així com la matèria, està formada per partícules. La llum i altres radiacions electromagnètiquesw1, per exemple, es componen de partícules anomenades fotons.
Imatge de Public Domain Imag
/Wikimedia
Anomenada en honor al físic alemany Max Karl Planck (1858-1947), la constant de Planck ens diu com es relaciona l’energia dels fotons individuals amb la longitud d’ona de la radiació, com mostra aquesta equació clau:
Ep = hc/λ
On Ep és l’energia d’un sol fotó (en joules), h és la constant de Planck, c és la velocitat de la llum en el buit, i λ és la longitud d’ona de la radiació.
Potser sorprèn que, tot i que el valor de la constant de Planck sigui extraordinàriament petit, hàgim desenvolupat un mètode de determinació d’aquest valor en un experiment d’aula. L’activitat no necessita cap equipament especial, només uns quants díodes emissors de llum de color (LEDs) i aparells elèctrics estàndard. Aquesta activitat és adequada per un ample ventall d’estudiants, des de l’edat d’uns 16 anys fins al nivell de postgrau.
Com funcionen els LEDs
Els LEDs es fabriquen per la unió de dos materials semiconductors “dopats”, un dels quals té un excés d’electrons (tipus n) i l’altre una manca d’electrons, també anomenats com a forats (tipus p). Quan es fa passar un corrent elèctric a través d’aquesta anomenada unió “p – n”, la recombinació d’electrons i forats allibera energia en forma de fotons.
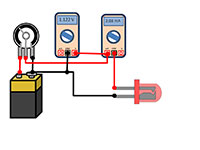
resposta voltatge-corrent de
cada LED. De esquerra a
dreta: bateria, potenciòmetre
o reòstat, voltímetre,
amperímetre, LED.
Imatge cortesia dels autors
El color de la llum emesa per un LED està determinat per l’energia dels fotons, i poden ser dissenyats canviant la composició química dels materials semiconductors. Els LEDs més comuns estan fets d’aliatges de gal·li, arsènic i alumini i, canviant la proporció d’aquests components, es poden produir LEDs que emetin llum de colors específics, com el vermell i el verd a la regió visible de l’espectre electromagnètic, o més enllà, en les regions de l’ultraviolat o l’infraroig.
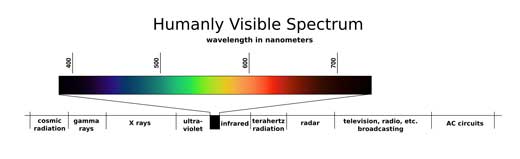
Com amb qualsevol llum, és la longitud d’ona la que determina el seu color. L’ull humà és sensible a la llum amb longituds d’ona al voltant de 390 a 700 nanòmetres (0,00039 – 0,007 mm). Veiem les longituds d’ona més curtes com a violeta i les més llargues com a vermell, i cada longitud d’ona d’entremig correspon a un color determinat en l’espectre. Per exemple, els LED de color verd, normalment produeixen llum amb una longitud d’ona d’uns 567 nanòmetres.
Utilitzem LEDs en aquest experiment perquè cada color del LED té un voltatge llindar diferent a la qual comencen a produir-se electrons. Mesurar aquest voltatge, juntament amb els valors coneguts per les longituds d’ona d’emissió, proporciona un camí per trobar un valor de la constant de Planck.
Materials
- Quatre LEDs que emetin llum de color, un de vermell, taronja, verd i blau. Trieu els LED amb una carcassa que l’envolti clara i incolora, de manera que el color de la llum provingui del propi dispositiu, no de l’embolcall de color.
- Bateria de 9 V.
- Dos multímetres (un per ser utilitzat com a voltímetre i l’altra com a amperímetre).
- Un potenciòmetre o reòstat d’1 k?.
Procediment
- Configureu el circuit com es mostra en el diagrama següent. Connecteu l’amperímetre en sèrie amb el LED per mesurar el corrent que el recorre, i connecteu el voltímetre en paral·lel al LED per mesurar el voltatge a través d’ell. La tensió aplicada es pot canviar mitjançant el potenciòmetre o reòstat.
- Canvieu el voltatge en increments de 0,05 V entre 0 V i 3 V, i mesureu el corrent elèctric resultant. Tingueu en compte que quan el corrent que circula a través del LED és petit, el LED podria no encendre’s, però l’amperímetre encara pot mesurar el corrent. Per protegir el LED, tingueu cura de mantenir el corrent per sota de 5 mA.
- Per a cada LED, dibuixeu un gràfic de la intensitat del corrent davant del voltatge, similar als gràfics que es mostren a l’esquerra. A cada gràfic, trobeu la línia recta de “millor ajust” per als punts que pugen cap amunt des de l’eix de les x. Si els punts es troben a prop de la línia, això demostra que hi ha una relació lineal entre la tensió aplicada i la intensitat del corrent en aquesta zona del gràfic.
- Finalment, determineu el voltatge d’activació (Va) a partir de les dades recollides. Aquest és el punt en què la intensitat del corrent comença a augmentar linealment amb la tensió. Es pot llegir del gràfic per extrapolació de la línia recta que representa la regió de resposta lineal fins que intercepta l’eix x. Els estudiants poden fer això visualment fent servir un regle, o matemàticament mitjançant l’aplicació de la regressió lineal dels punts de dades experimentals en la regió linealw2.
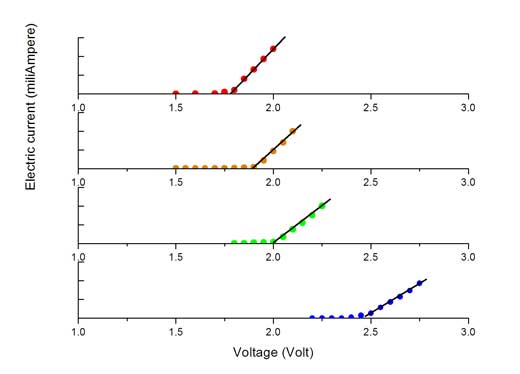
Imatge cortesia dels autors
Per obtenir valors més precisos de Va per a cada color de LED, es pot calcular un valor mitjà utilitzant els resultats obtinguts per diversos alumnes.
Valors típics per a tensions d’activació obtinguts mitjançant aquest experiment es mostren a la dreta, juntament amb els valors de longitud d’ona de la llum emesa pels LEDs de colors. Vostè pot proporcionar als alumnes aquests valors de la longitud d’ona per a la propera etapa de l’activitat a l’aula. Alternativament, les longituds d’ona es poden mesurar utilitzant un espectròmetre casolà, com el que es descriu en el següent recurs webw3.
| Color del LED | Longitud d’ona típica, λ (cm) | Voltatge d’activació, Va (V) |
|---|---|---|
| Vermell | 623 | 1.78 |
| Taronja | 586 | 1.90 |
| Verd | 567 | 2.00 |
| Blau | 567 | 2.45 |
Imatge cortesia de entirelysubjective/Flickr
Anàlisi i resultats
Com hem vist abans, l’energia dels fotons emesos, Ep (mesurada en joules), està relacionada amb la constant de Planck (h), la velocitat de la llum en el buit (c)i la longitud d’ona de la llum λ :
Ep = hc/λ (1)
En aquest experiment, tenim un rang de valors per ? de les longituds d’ona conegudes de la llum de colors dels LED, i sabem el valor de c (2.9979 x 108 ms-1). Però com fem servir els nostres valors obtinguts experimentalment de Va per calcular la constant de Planck? Per esbrinar-ho, anem a considerar el que està succeint dins dels LED.
Quan els LED estan operant a valors baixos de voltatge, l’entrada d’energia no és suficient per produir fotons i el corrent elèctric és molt petit. A un determinat voltatge, el LED comença a emetre fotons: aquesta és la tensió d’activació, Va. Aquesta tensió mínima per a cada color de LED es correlaciona amb l’energia dels fotons emesos, Ep (equació 2). I de fet, igual que Ep, Va està matemàticament relacionada amb la constant de Planck i la longitud d’ona de la llum emesa, com es mostra en la següent equació:
Va = Ep/e + φ/c (2)
On e és la càrrega de l’electró (1.6022 x 10-19 coulombs). Per a voltatges superiors a Va el corrent elèctric està determinat per la resistència interna del LED. De la llei d’Ohm, voltatge = intensitat x resistència, hi ha una relació lineal entre el corrent elèctric i el voltatge aplicat, com es veu en els gràfics voltatge-corrent anteriors.

cúpules a la riba del riu
Swan, Perth, Australia
Occidental
Imatge cortesia de
Gnangarra/Wikimedia
En l’equació 2, el terme (φ/c) és una constant que fa referència a les pèrdues d’energia a l’interior de la unió p – n dels semiconductors. (Per simplificar, podem assumir que aquesta constant ha de ser igual per a tots els LED). Donat que ? és desconeguda no és possible a partir de l’equació 2 determinar la constant de Planck mesurant solament el voltatge d’activació. No obstant això, si es mesura el voltatge d’activació per a uns quants LEDs que emeten a diferents longituds d’ona conegudes, llavors podem trobar un valor de h mitjançant el traçat d’un gràfic de Va en funció del recíproc de la longitud d’ona (1/λ).
Això és perquè reordenant (2) dóna aquesta equació:
Va = hc/e(1/λ) + φ/c (3)
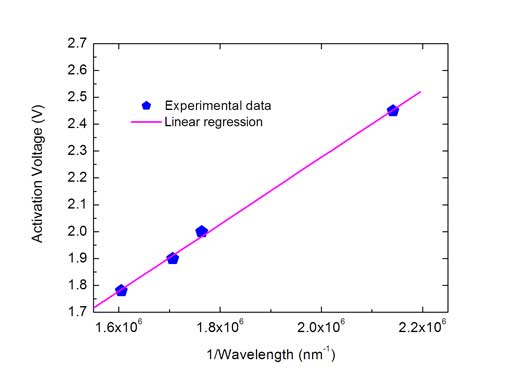
Així, el gràfic de Va davant 1/λ prendrà la forma d’una línia recta amb un pendent igual a hc/e, a partir del qual es pot calcular fàcilment la constant de Planck, a partir dels valors coneguts de e i c. Aquest gradient es pot trobar gràficament traçant el gràfic i dibuixant una línia de millor ajust a les dades, o matemàticament fent servir un calculador de regressió linealw2.
La regressió lineal dóna el següent valor per al gradient (m): m = 1.24811 x 10-6 Vm (volt metre) A partir d’aquí finalment es pot calcular la constant de Planck. D’abans, m = hc/e, així:
h = em/c (4)
= 1.6022 x 10-19 x 1.24811 x 10-6/2.9979 x 108
= 6.6704 x 10-34 Js (joule segon)
Imatge cortesia dels autors
Aquest valor és comparable amb el valor acceptat per la constant de Planck de 6.62606957 x 10-34 Js, amb un error de tant sols el 0,7 per centw4. Els valors obtinguts pel seus estudiants poden ser una mica més grans d’aquest valor, però encara han de proporcionar una aproximació satisfactòriament bona a una de les constants fonamentals de la natura
Web References
- w1 – Per obtenir més informació sobre la llum i l’espectre electromagnètic, vegeu:
-
Mignone C., Barnes R. (2011) More than meets the eye: the electromagnetic spectrum. Science in School 20:51-59.
-
- w2 – Calculadores de regressió lineal en línia que poden ajudar a analitzar les seves dades:
- w3 – Per aprendre a construir el seu propi espectròmetre, veure:
-
Tiele Westra M. (2007) A fresh look at light: build your own spectrometer. Science in School 4:30-34.
-
- w4 – Al National Institute of Standards and Technology (NIST) hi ha el valor de referència disponible per a la constant de Planck.
Resources
- El projecte “Sixty Symbols” de la Universitat de Nottingham ha produït un vídeo curt que explica la importància de la constant de Planck, que es pot trobar a.
Review
Aquest article presenta un experiment senzill i pràctic que es pot utilitzar per verificar el valor de la constant de Planck, que és àmpliament utilitzada en la física quàntica. El muntatge és fàcilment reproduïble a classe, ja que els materials utilitzats es troben normalment en els laboratoris de física. Per tant es pot utilitzar com una demostració a classe o com una investigació realitzada pels propis estudiants.
La teoria involucrada en aquest tema pot inicialment semblar abstracta d’entendre per als estudiants, però aquest experiment els ajudarà a aclarir alguns conceptes i comprendre millor les teories involucrades. L’article i l’experiment mostren alguns conceptes molt importants, com ara:
- l’efecte fotoelèctric, on “paquets d’energia” són absorbits per un material i per tant causen que el diode emeti ones electromagnètiques;
- la tensió d’activació en díodes;
- càlcul de la constant de Planck.
Catherine Cutajar, Malta





