Pomiary nieba z użyciem smartfona Teach article

Tłumaczenie Ewa Stokłosa. Twoi uczniowie użyją smartfonów w pomiarach astronomicznych.

Gdzie dokładnie znajdujesz się w tym momencie? Możesz się tego dowiedzieć dzięki systemowi nawigacji satelitarnej (często zwanemu GPS) na smartfonie. Jednak kiedyś to gwiazdy wskazywały położenie obserwatora – szczególnie pomagały one marynarzom na morzu, które pozbawione jest punktów charakterystycznych.

W artykule opisujemy pierwsze osiągnięcia w nawigacji wykorzystujące położenie gwiazd i pokazujemy, jak owe tradycyjne techniki można wykorzystać podczas lekcji przy pomocy prostych aplikacji na smartfonie. Uczniowie mogą następnie użyć systemu GPS, również na smartfonie, aby sprawdzić dokładność swoich pomiarów oraz zastanowić się nad źródłami potencjalnych błędów.

Oba zaprezentowane poniżej ćwiczenia są odpowiednie dla uczniów w wieku 14-18 lat i wykorzystują wiedzę z zakresu historii, astronomii, geografii i matematyki: wyznaczanie szerokości geograficznej (ryc. 1) z pomocą Słońca oraz Gwiazdy Polarnej. Szczegóły międzyszkolnego ćwiczenia, którego celem jest wspólne obliczenie obwodu Ziemi, można pobrać z części materiały dodatkowe. Do wykonania tych trzech ćwiczeń potrzeba niewiele więcej poza smartfonem, a każde z nich zajmie nie dłużej niż godzinę.

Wyznaczanie szerokości geograficznej poprzez wysokość Słońca

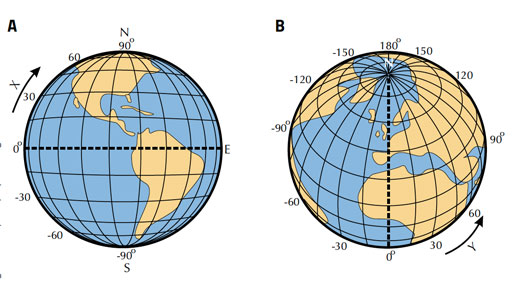
„Czym jest południe?” to być może dziwne pytanie. Czyż nie jest to po prostu godzina 12 w południe? Jednak mówiąc ściśle, południe słoneczne to moment, w którym Słońce przechodzi przez twój południk, czyli linię długości geograficznej, na której się znajdujesz, i zwykle będzie się ono wtedy znajdować trochę na północ lub trochę na południe. Słońce będzie wówczas w najwyższym punkcie na niebie, a cienie będą najkrótsze. Właśnie w tym momencie można wykorzystać pozycję Słońca do wyznaczenia długości geograficznej swojego położenia, czyli kątowej odległości od równika.

Jak to działa? Przyjrzyjmy się sytuacji podczas jednej z równonocy (około 20 marca lub 23 września każdego roku), kiedy to płaszczyzna równika przebiega przez środek Słońca (ryc. 2).

• A: Wyobraź sobie, że jesteś na równiku, szerokość geograficzna 0°, w południe: Słońce znajduje się dokładnie nad twoją głową (w zenicie). Gdybyś zmierzyła wysokość Słońca (czyli kąt pomiędzy Słońcem a horyzontem), okazałoby się, że wynosi ona 90° (ryc. 3A). Odejmując tę liczbę od 90° otrzymujemy 0°, czyli twoją szerokość geograficzną.

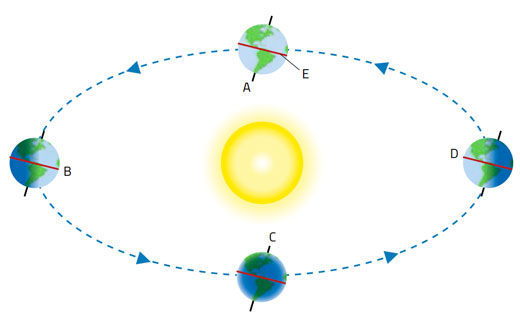
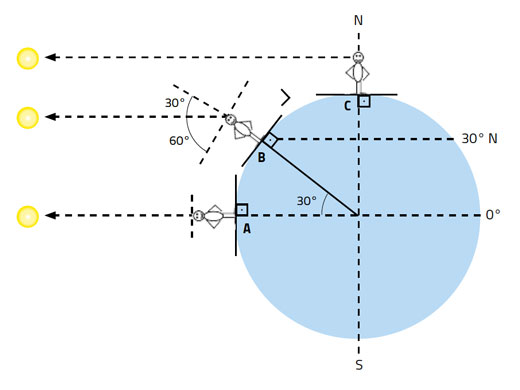
(Powiedzieliśmy, że Słońce zwykle położone jest w kierunku północnym lub południowym. Podczas równonocy znajduje się w zenicie.)

• B: Twoja koleżanka znajduje się na biegunie północnym lub południowym (szerokość odpowiednio 90° N lub 90° S). W tym samym momencie widzi, że Słońce znajduje się dokładnie na horyzoncie: na wysokości 0° (ryc. 3B). Odejmując tę wartość od 90° otrzymujemy 90°, czyli jej szerokość geograficzną.
• C: Twój kolega znajduje się na tym samym południku co ty, ale na szerokości 30° N. Ponieważ to ten sam południk, dla niego również jest południe, ale zaobserwuje on Słońce na wysokości 60° nad horyzontem (ryc. 3C). Odejmując tę wartość od 90° otrzymujemy 30°: jego szerokość geograficzną.

Szerokość geograficzna = 90° – wysokość Słońca nad horyzontem w południe podczas równonocy                        (Równanie 1)

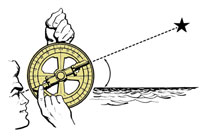
Jak możemy wykorzystać tę wiedzę w praktyce? W wieku XV i na początku XVI wielu nawigatorów korzystało z żeglarskich astrolabiów, dzięki którym mierzyli oni wysokość Słońca nad horyzontem i w ten sposób obliczali szerokość geograficzną statku. Astrolabium było swego rodzaju inklinometrem: zawieszano je w pionowej płaszczyźnie i celowano nim w ciało niebieskie, na przykład Słońce. Ruchoma alidada służyła do odczytania wysokości ciała nad horyzontem z podziałki znajdującej się na zewnętrznym pierścieniu.

Astrolabium jest co prawda łatwe w wykonaniu^w2, ale równie proste jest użycie smartfona z aplikacją inklinometr do pomiaru wysokości Słońca nad horyzontem. Jednak zanim do tego przejdziemy, musimy wprowadzić pewną poprawkę, aby nasze obliczenia mogły być wykonywane przez cały rok.

Z powodu nachylenia osi obrotu Ziemi (23,45°) oraz faktu, że Ziemia krąży wokół Słońca, jedynie podczas równonocy Słońce pojawia się dokładnie nad równikiem. Po równonocy wiosennej pozycja Słońca zmienia się i wydaje się ono przesuwać na północ od równika, otrzymując maksymalny kąt odchylenia +23,45° podczas przesilenia letniego, powracając do odchylenia 0° podczas równonocy jesiennej, a następnie przesuwając się na południe, aż uzyskuje kąt odchylenia -23,45° podczas przesilenia zimowego. Kąt ten nazywany jest deklinacją słoneczną (ryc. 5).

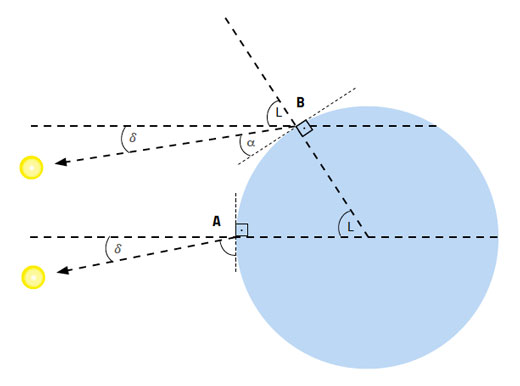
Dlatego mierzona przez wczesnych nawigatorów z użyciem astrolabium i mierzona przez nas smartfonem wysokość Słońca nad horyzontem w południe zależy zarówno od dnia w roku – stąd deklinacja słoneczna – jak i od naszej szerokości geograficznej (ryc. 6):

Wysokość Słońca w południe = 90° + deklinacja – szerokość geograficzna             (Równanie 2)

Lub:

Szerokość geograficzna = wysokość Słońca w południe + deklinacja                       (Równanie 3)

Aby ustalić deklinację Słońca pierwsi nawigatorzy korzystali z tabel lub zaawansowanych astrolabiów, które na obrotowej płycie miały wypisane odpowiednie wartości. My możemy te same dane uzyskać z aplikacji planetarium, co umożliwi pomiar wysokości Słońca i wyznaczenie naszej szerokości geograficznej.

Materiały

Każda grupa uczniów potrzebuje:

• Smartfona z aplikacjami inklinometr i planetarium
• Słomkę do napojów
• Taśmę klejącą
• Poziomicę (opcjonalnie)

Procedury

Aby wyznaczyć swoją szerokość geograficzną należy:

1. Zamocować słomkę do brzegu smartfona przy użyciu taśmy klejącej (ryc. 7). To alidada.
2. Przy pomocy aplikacji planetarium ustalić lokalny moment południa słonecznego oraz deklinację słoneczną.

W zależności od waszej lokalizacji w danej strefie czasowej, południe słoneczne może mieć miejsce już o 11.30, a ze względu na stosowanie czasu letniego, nawet o 13.30.

3. Trzymając smartfona ze słomką na wierzchu wycelować nią w Słońce. Smartfon jest poprawnie ustawiony, gdy cień słomki jest możliwie najmniejszy (ryc. 7).
4. Przy użyciu aplikacji inklinometr odczytać kąt wysokości Słońca nad horyzontem.
5. Użyć równania 2 do obliczenia szerokości geograficznej.

Aby móc ustawić smartfony jeszcze dokładniej w kierunku Słońca i precyzyjniej zmierzyć jego wysokość, uczniowie mogą ewentualnie zbudować podstawkę i umieścić ją na statywie. Szczegóły i materiały do konstrukcji dostępne są online^w3.

Dyskusja

Poproś uczniów, aby porównali swoje wyniki z dokładną szerokością geograficzną podaną przez system GPS na ich smartfonie lub przez aplikację planetarium. Jak dokładny wynik otrzymali? Jakie mogły być przyczyny błędów?

Dokładność obliczeń wynika oczywiście z precyzji pomiarów, np. na ile dokładnie uczniowie przymocowali słomkę wzdłuż brzegu smartfona lub czy cień słomki był rzeczywiście minimalny. Aby uzyskać najdokładniejsze wyniki, pomiary powinny być dokonane w południe, jednak kilka minut przyspieszenia lub opóźnienia nie będzie miało wpływu na ostateczny rezultat, ponieważ gdy Słońce znajduje się najwyżej, jego pozorny ruch jest najwolniejszy.

Smartfony mogą mierzyć kąt nachylenia z dokładnością do 0,1°, czyli dosyć precyzyjnie. Można jednak skalibrować aplikację inklinometr z poziomicą, aby sprawdzić, czy wartość 0,0° rzeczywiście pokrywa się z horyzontem.

Możesz również zapytać uczniów, dlaczego wyznaczanie długości geograficznej stało się możliwe dopiero w XVIII wieku, skoro szerokość określano o wiele wcześniej.

Odpowiedź tkwi w obrotowym ruchu Ziemi: 360° na jedną dobę to około 15° na godzinę. Dlatego porównując czas lokalny z czasem miejsca w punkcie odniesienia o znanej długości geograficznej, możliwe jest wyznaczenie długości geograficznej punktu, w którym się znajdujemy. Czas lokalny można oszacować na podstawie położenia Słońca, ale problemem był czas punktu odniesienia: zegar precyzyjnie odmierzający czas nawet na pokładzie płynącego statku został wynaleziony dopiero w 1759 roku przez Johna Harrisona.

Wyznaczanie szerokości geograficznej poprzez wysokość Gwiazdy Polarnej

W poprzednim ćwiczeniu mierzyliśmy wysokość Słońca w południe: gdy Słońce przecina Twój południk. W tym momencie Słońce wydaje się być odrobinę na północy lub południu. Gdyby uczniowie próbowali obliczyć swoją szerokość geograficzną o innej porze dnia, otrzymane wyniki mogłyby być całkowicie błędne. Na szczęście istnieje inna metoda, która nie jest aż tak zależna od czasu – choć działa tylko na półkuli północnej i trzeba ją zastosować po zmroku – a jest nią obserwacją Gwiazdy Polarnej.

Pozycje innych gwiazd pozornie zmieniają się z upływem godzin, jednak Gwiazda Polarna wydaje się być uwiązana do północy (ryc. 8), ponieważ jest umiejscowiona na przedłużeniu osi obrotu Ziemi. Gdybyśmy stanęli na biegunie północnym (szerokość geograficzna 90°), Gwiazda Polarna świeciłaby dokładnie nad naszymi głowami, na wysokości 90°. Zupełnie inaczej byłoby na równiku (szerokość geograficzna 0°), gdzie znajdowałaby się ona na horyzoncie (na wysokości 0°). Dlatego wysokość Gwiazdy Polarnej jest równa naszej szerokości geograficznej: gdybyśmy byli w Paryżu, na szerokości około 49° N, Gwiazda Polarna znalazłaby się na wysokości około 49°.

Szerokość geograficzna = wysokość Gwiazdy Polarnej                                (Równanie 4)

Pierwsi nawigatorzy korzystali z astrolabium, aby kierować się gwiazdami w nocy, tak jak robili to ze Słońcem w dzień. W tym ćwiczeniu ponownie możemy użyć smartfona.

Materiały

• Smartfon z aplikacjami inklinometr i planetarium
• Lornetka (opcjonalnie)
• Latarka (opcjonalnie)

Procedury

Łatwiej jest wyznaczyć szerokość geograficzną poprzez wysokość Gwiazdy Polarnej niż Słońca: nie trzeba uwzględniać deklinacji, bo pozycja Gwiazdy Polarnej nie ulega zmianie przez cały rok.

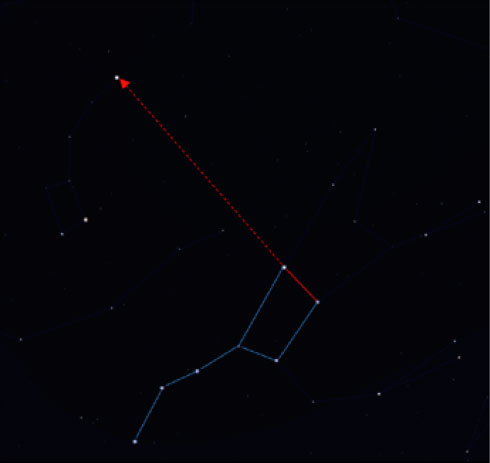
Jak odnaleźć Gwiazdę Polarną? Poszukaj gwiazdozbioru Wielkiej Niedźwiedzicy (ryc. 9). Przedłuż wyobrażoną linię, łączącą dwie ostatnie gwiazdy czworokąta, w górę, odkładając wzdłuż tej linii mniej więcej siedmiokrotną odległość między tą parą gwiazd. Pierwsza jasna gwiazda, do której dotrzesz to Gwiazda Polarna należąca do gwiazdozbioru Małej Niedźwiedzicy. Możesz również skorzystać z funkcji wyszukiwania w aplikacji planetarium.

Gwiazda Polarna jest zdecydowanie słabsza od Słońca, więc można obserwować ją bezpośrednio, bez alidady, jednak jej niska jasność utrudnia też jej zlokalizowanie. Pomocne może być przećwiczenie umiejętności mierzenia wysokości obiektów na jaśniejszych ciałach, np. planetach czy Księżycu.

Należy:

1. Ustawić smartfon dłuższym brzegiem do góry, a następnie wskazać nim dokładnie na Gwiazdę Polarną, spoglądając na ściankę telefonu.

Potrzebne będzie oświetlenie, aby dostrzec brzeg telefonu w ciemności.

2. Przy użyciu aplikacji inklinometr odczytać wysokość Gwiazdy Polarnej nad horyzontem. Jest to szacunkowa szerokość geograficzna.

Uczniowie mogą również pracować w parach i użyć lornetki. Uczennica ustawia lornetkę na Gwiazdę Polarną w taki sposób, aby znalazła się ona w centrum pola widzenia (można położyć lornetkę na przykład na murze, aby była nieruchoma). Uczeń przykłada smartfona do lornetki i odczytuje wysokość gwiazdy. Jeśli jest taka potrzeba, należy skalibrować lornetkę: położyć ją na poziomej powierzchni, na niej umieścić smartfona i odczytać kąt z aplikacji inklinometr.

Dyskusja

Poproś uczniów, aby odczytali wysokość Gwiazdy Polarnej z aplikacji planetarium. Jak dokładny był ich pomiar? Jak ma się oszacowana przez nich szerokość geograficzna względem dokładnej szerokości podawanej przez nawigację GPS lub aplikację planetarium? Jakie według nich mogły być przyczyny błędu, poza omawianymi przy poprzednim ćwiczeniu?

Mimo względnej jasności, Gwiazda Polarna jest zdecydowanie ciemniejsza niż Słońce, co utrudnia uzyskanie dokładnego odczytu jej wysokości.

Innym źródłem błędu może być pozycja Gwiazdy Polarnej. Powiedzieliśmy wcześniej, że na biegunie północnym wydawałaby się ona znajdować dokładnie nad głową: na wysokości 90°. Jednak wysokość ta wyniosłaby 89,3°, co wprowadza błąd o 0,7° do obliczeń uczniów, który to błąd równa się około 100 km.

Opisana metoda sprawdza się najlepiej na średnich szerokościach geograficznych. Daleko na północ trudno jest wycelować w gwiazdę, która jest niemal dokładnie nad głową. W okolicach równika Gwiazda Polarna znajduje się blisko horyzontu, gdzie atmosfera ziemska jest bardziej zaburzona.

Podziękowania

Artykuł oparty jest na ćwiczeniu opublikowanym przez Science on Stage, sieć dla europejskich nauczycieli przedmiotów ścisłych, technologii, inżynierii i matematyki (STEM), która została zainicjowana w 1999 roku przez EIROforum, wydawcę czasopisma Science in School. Science on Stage łączy nauczycieli przedmiotów ścisłych z całej Europy, którzy dzielą się pomysłami i najlepszymi praktykami w entuzjastycznymi kolegami z 25 krajów.

Podczas warsztatów Science on Stage w Wiedniu i Berlinie, jak również w dyskusjach prowadzonych drogą mailową oraz na otwartej platformie e‑learningowej Moodle, 20 nauczycieli z 14 europejskich krajów wspólnie stworzyło 11 modułów nauczania pokazujących jak smartfony i aplikacje mogą być wykorzystywane na lekcjach matematyki, fizyki, chemii i biologii. Moduły te zostały opublikowane w 2014 roku przez Science on Stage Germany jako iStage 2: Smartphones on Science Teaching^w4. Projekt jest wspierany przez SAP. 

Oprócz Gerharda Ratha oraz Philippe’a Jeanjacquota, w projekt zaangażowani byli również Pere Compte z Hiszpanii i Immacolata Ercolino z Włoch. Martin Pratl udzielił cennej pomocy przy tekście do artykułu.