Giocare agli scienziati: insegnare le abilità di processo della scienza Teach article
Può accadere che, nella grande abbondanza di dettagli della scienza moderna, ci si dimentichi del fattore unificante: il metodo scientifico. Alfredo Tifi, Natale Natale e Antonietta Lombardi spiegano come incoraggiare le abilità di investigazione scientifica, quali la produzione di ipotesi e il…
Le abilità di processo sono fondamentali per la scienza in quanto permettono a chiunque di condurre indagini e raggiungere conclusioni. Siamo convinti che ci sia un grave gap educativo in questo settore, sia nel portare queste abilità nella classe, sia nel formare gli insegnanti in funzione di questo obiettivo. È ovviamente un problema con molte sfaccettature, che coinvolge l’amministrazione scolastica e i canali della formazione dei docenti, ma anche lo sviluppo delle abilità sociali di cui necessitano gli studenti per collaborare efficacemente, per condividere, dibattere, sostenere ed estendere le idee nei gruppi di indagine. Al fine di facilitare l’introduzione di alcuni principi della ricerca scientifica, abbiamo sviluppato dei percorsi di attività di laboratorio utilizzabili principalmente nella scuola primarie e secondaria di primo grado.
La maggior parte delle lezioni sperimentali di scienze sono basate sui contenuti: per esempio, “determinare le variabili che influenzano la crescita delle piantine di fagiolo”. Quand’anche queste esperienze siano ben impostate, i contenuti molto spesso prevalgono sul processo di investigazione, impedendo così agli studenti di estrapolare principi generali – relativi al metodo scientifico – da ciò che stanno facendo. Per sviluppare modalità di pensiero scientifico, gli studenti necessitano di “opportunità ripetute di lavorare impiegando tali abilità in contesti diversi e su contenuti diversificati”w1.
Per questo il nostro approccio è consistito nel creare dei “giochi” di laboratorio liberi da contenuti, dove poter concentrare l’attenzione sul processo piuttosto che su contenuti particolari. Le abilità di processo, una volta conquistate, resistono all’usura del tempo meglio delle conoscenze di particolari contenuti scientifici e riteniamo che attività investigative manipolative (hands-on), centrate sul metodo, debbano diventare una componente rilevante dell’insegnamento delle scienze, allo stesso livello delle attività concrete basate sul contenuto, piuttosto che essere entrambe bistrattate anche nelle scuole più “fortunate” dal punto di vista delle sperimentazioni metodologiche.
Dalle attività basate sul contenuto alle ‘black box’
Nel passato il nostro gruppo ha disegnato attività di laboratorio hands-on basate sui contenuti: dai materiali e le loro proprietà, alle interazioni, i sistemi e l’energia. Ispirati al programma SCIIS (Science Curriculum Improvement Innovatio Study), oltre ai termini chiave elencati, abbiamo elaborato unità didattiche sui concetti di variabile, modello e teoria, ma senza essere da subito consapevoli che tali attività riguardassero principalmente l’ambito dei processi tipici della ricerca scientifica. Durante le nostre attività sulla costruzione di modelli abbiamo scoperto che:
- Studenti di 8-12 anni considerano sfidanti, oltre che divertenti, le attività altamente impegnative di investigazione proposte che richiedevano la costruzione di modelli.
- Anche gli allievi più piccoli, impegnando grandi dosi di immaginazione, producevano ipotesi fondate riguardanti problemi rilevanti.
Abbiamo concluso che l’indagine scientifica può costituire la parte più attraente della scienza, per gli studenti di ogni età, e che l’immaginazione permette ai bambini di compiere comunque processi astrattivi.
Quindi negli ultimi due anni ci siamo concentrati sullo sviluppo di attività che richiedevano agli studenti di investigare sistemi o fenomeni “chiusi” in “scatole nere”, con il compito di evidenziare le regolarità, sviluppare spiegazioni e costruire modelli capaci di riprodurre il comportamento di tali “scatole nere”: osservando, facendo inferenze, predizioni, controllando le variabili, ipotizzando, pianificando e conducendo esperimenti.
Le “scatole nere” devono essere adattate alle età dei bambini e al livello delle classi. Sono di seguito illustrati alcuni esempi.
Classi prima e seconda (6-8 anni)
I bambini scuotono un barattolo metallico sigillato. Lo soppesano, ne ascoltano i suoni, cercando di indovinare quali materiali o oggetti vi sono contenuti. Questo gioco ha anche una versione software, per studenti più grandi, in cui un oggetto nascosto deve essere identificato attraverso test simulati di schiacciamento in una pressa, diluizione con un solvente magico che ne scioglie il colore, infiammabilità, pesata alla bilancia, esposizione a “raggi X”, profilo sonar da due diverse direzioni perpendicolari, test di magnetismo con calamitaw2.
I bambini di seconda-terza elementare possono anche utilizzare le macchine operatrici descritte più avanti.
Classe terza (8-9 anni)
Nel ‘gioco del circuito’ gli studenti hanno a disposizione un rivelatore auto-costruito – con una batteria e una lampadina – e con esso uniscono dei contatti esterni per verificare la presenza di collegamenti nascosti all’interno di un cartoncino piegato in due. Si apre il cartoncino per comparare la rete dei collegamenti reale (formata da strisce di alluminio incollate) con il modello disegnato dai bambini – sulla base delle risultanze sperimentali, e si scopre con disappunto che tra le due ci sono alcune differenze!
Classe quarta (10-11 anni)
Il gioco del ‘dado nella scatola’ è formato da una scatola con una finestra traslucida, dalla quale è possibile vedere una sola faccia per volta di un dado variamente colorato in essa contenuto. Gli studenti devono lanciare il dado nella scatola al fine di dedurre quante facce vi sono in esso per ciascun colore e infine disegnare un modello aperto –bidimensionale. Si dimostra così ai bambini che gli scienziati hanno bisogno di disegnare modelli quando sono incapaci di esaminare direttamente gli oggetti reali. Si può portare come esempio il fatto che il nucleo del pianeta Terra è soltanto un modello ricavato da studi sul modo con cui le onde sismiche sono riflesse a una certa profondità, cosa che ha permesso di dedurre la presenza di una discontinuità.
Classe quinta – Scuola secondaria di I grado (11-14 anni)

tappi di bottiglia
Negli esperimenti sui pattern gli studenti devono trovare andamenti regolari tra variabili correlate. Per esempio, negli schieramenti triangolari di tappi, essi devono determinare la relazione esistente tra i numeri di tappi posti lungo il lato e i numeri di tappi in totale.
Utilizzando una Slinky®, gli studenti cercano di determinare la relazione tra il ritmo delle oscillazioni e il numero di spire che si lasciano libere di oscillare. In un altro esperimento, essi deducono, in base all’allungamento della molla, quante monete sono state caricate nel piattello alla sua base. Utilizzando corde di chitarra essi cercano di determinare la relazione tra tensione e tono.
In questi ed altri esperimenti gli studenti utilizzano grafici o relazioni matematiche empiriche, per compiere predizioni, senza ricorrere a spiegazioni meccanicistiche basate su leggi fisiche.
Sperimentazioni in corso
Grazie ad alcuni insegnanti che svolgono formazione in servizio e ad altri tutor volontari, stiamo mettendo alla prova una varietà di strumenti con gli studenti. Saremmo entusiasti di ricevere un supporto da parte di un’istituzione di ricerca educativa, per poter arrivare a progettare e implementare un’attività di formazione sistematica rivolta agli insegnanti in pre-servizio o in servizio. Nel rivalutare la formazione degli insegnanti, si dovrebbero mettere al primo posto i principi della scienza come processo, in linea con i progetti Europei che mirano all’introduzione, nell’educazione scientifica, di metodologie basate sull’enquiryw3,w4.
Macchine operatrici
Questi giochi coinvolgono ‘macchine trasformatrici che si alimentano di oggetti in input ed ‘espellono’ elementi processati dello stesso tipo’. Tali elementi possono essere ‘blocchi logici’ o numeri interi.
Macchine a blocchi logici: ideali per seconda–terza elementare
Questa attività fa uso di blocchi logici colorati – una confezione tipica italiana contiene 48 pezzi (quattro forme, tre colori, due dimensioni e due spessori). Ogni ‘macchina trasformatrice di blocchi logici’ modifica uno o due attributi per volta secondo una regola fissa. Per esempio, la regola di trasformazione potrebbe essere ‘TUTTI i blocchi rossi O spessi diventano gialli E grandi’. Gli altri blocchi rimangono invariati passando attraverso la macchina. La classe conduce esperimenti per dedurre il meccanismo sconosciuto. L’indagine comporta una serie di prove, un’analisi dei risultati, la formulazione di ipotesi, la verifica o smentita di queste e la creazione di modelli più o meno stabili per il meccanismo di trasformazione.

macchine trasformatrici di
blocchi logici
Il gioco si introduce in classe con uno studente che funge da ‘macchina trasformatrice virtuale’, mantenendo la regola nella sua mente. Il meccanismo di trasformazione può essere ideato dallo studente o può essere estratto da un mazzo di cartoncini con meccanismi diversi preparati precedentemente. Gli altri bambini svolgono invece la funzione di ricercatori con lo scopo di investigare, proporre esperimenti, predire il risultato delle trasformazioni. Lo studente che funge da meccanismo mette all’interno della scatola un vero blocco logico in ingresso ed estrae il blocco in uscita, processato, dall’altro lato, seguendo fedelmente il criterio assegnato.
Gli studenti possono a questo punto passare alla versione software, MOBL (Macchina Operatrice a Blocchi Logiciw5). L’interfaccia dell’applicazione può anche essere proiettata sullo schermo mentre la classe affronta il problema come se fosse un team di scienziati. In presenza di un numero sufficiente di computer a disposizione si può disporre la classe anche in gruppi di investigazione di tre – quattro bambini.
Macchine operatrici numeriche
Queste macchine hanno numeri interi come input e output. Le trasformazioni coinvolgono in questo caso le quattro operazioni elementari, comparazioni pari-dispari, maggiore-minore, uguaglianza, il modulo e, a livelli di maggior complessità, combinazioni di queste operazioni.
Per introdurre le macchine operatrici numeriche, gli studenti possono simulare la macchina, come descritto per i blocchi logici.
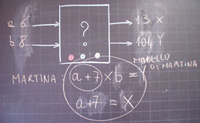
Dopo un’esperienza molto incoraggiante realizzata con solo gesso e lavagna, abbiamo sviluppato tre tipi di macchine softwarew6, MO11, MO12 e MO21, dove la parte numerica dei nomi indica il numero di input e di output. MO21 è la più interessante, poiché offre l’opportunità di controllare due variabili sperimentali (Tabella 3). Attualmente stiamo sviluppando versioni online delle macchine operatrici. Gli insegnanti e gli alunni possono scegliere il più appropriato livello di complessità del meccanismo che attua la trasformazione dei numeri adattabile dalla seconda elementare alla scuola superiore di secondo grado.
Queste applicazioni permettono agli studenti di salvare il meccanismo generato in modo casuale e di ricaricarlo in seguito, consentendo di condividere o trasmettere ad altri ‘team di scienziati’ le ricerche più ostiche. Con questa opzione desideriamo incoraggiare la perseveranza e l’attivazione di strategie cooperative, caratteristiche basilari dell’impresa scientifica. Le seguenti tabelle mostrano esempi di esperimenti condotti sulle MO e dei relativi risultati sperimentali.
| INPUT | 3 | 5 | 8 | 4 | 1 |
|---|---|---|---|---|---|
| OUTPUT | 4 | 8 | 14 | 6 | 0 |
Man mano che gli studenti utilizzano le macchine operatrici, essi scoprono che i modelli devono essere modificati in seguito all’acquisizione di nuove evidenze. Per esempio ci sono diversi modi per spiegare la Tabella 1:
- Output = input + (input – 2)
- Output = (2 x input) – 2
I bambini di differenti età affrontano questi modelli in modo completamente diverso – innanzitutto i bambini della scuola primaria non ragionano, evidentemente, in termini algebrici. In secondo luogo, il modello a) è fuori dalla portata dei bambini perché essi, con input inferiori a due, sono incapaci di calcolare (1 – 2) o (0 – 2).
Nel guidare queste attività, gli insegnanti devono concentrarsi nella cattura e sottolineatura dei principi generali che emergono da questa attività: gli studenti devono divenire consapevoli delle abilità e dei principi che utilizzano e dovrebbero parlare di questi, utilizzando termini generali come variabile, risultato, predizione, evidenza, esperimento, verifica, ipotesi, conferma, modello ecc. L’utilizzo di questo vocabolario rende conto per almeno il 50% delle abilità di processo e della metacognizione; l’altro 50% risiede nell’applicazione costante di queste abilità in attività di problem solving autentico.
Alcuni principi basilari emergenti, riferibili ad abilità di processo delle scienze sono:
- In ogni esperimento devono essere registrati i dati in ingresso e in uscita.
- Il primo approccio ad un fenomeno nuovo richiede osservazioni ed esplorazioni a ‘tutto campo’.
- Gli esperimenti dovrebbero essere condotti seguendo un piano sistematico.
- Gli esperimenti dovrebbero essere presentati in accordo a un criterio ordinatore preciso; alcune presentazioni dei dati sono migliori di altre per aiutare l’investigatore a riconoscere una regolarità.
- Coerenza: un modello efficace dovrebbe essere in accordo con tutti gli esperimenti, ovvero non si dovrebbe produrre un modello diverso per ciascuna evidenza sperimentale dello stesso fenomeno.
| INPUT | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| OUTPUT | 0 | 2 | 4 | 6 | 8 |
| INPUT | 2;1 | 2;2 | 2;3 | 3;2 | 1;2 |
|---|---|---|---|---|---|
| OUTPUT | 3 | 4 | 5 | 4 | 4 |
Marchingegni
I marchingegni si basano sullo stesso principio ideatore delle macchine operatrici, ma essi sono dei concreti congegni chiusi in una scatola, e dotati di almeno due parti mobili esterne che possono essere utilizzate come ‘input’ ed ‘output’. Le parti esterne possono costituite da fili colorati, manopole o aste rotanti, barre estraibili o leve pieghevoli. Tali parti manipolabili possono essere accoppiate attraverso un meccanismo interno di pulegge, leverismi, ingranaggi, cinghie e ruote, inaccessibili all’osservazione diretta.
Proponi I tuoi marchingegni!
Nel prossimo numero di Science in School, Alfredo Tifi, Natale Natale e Antonietta Lombardi descriveranno alcuni dei marchingegni che hanno sperimentato in classe e forniranno istruzioni dettagliate per la loro costruzione. Nel frattempo, perché non inviare vostre idee e progetti per marchingegni adatti a sviluppare le abilità di processo negli studenti?
Commenti finali
Saremmo ben lieti, con questo progetto, di suscitare idee simili e di stimolare discussioni sull’impostazione del laboratorio di scienze centrato sul metodo. Siamo convinti che un ingrediente fondamentale del fare scienza – lo sviluppo delle abilità di processo – dovrebbe essere insegnato inizialmente tramite attività di investigazione prive di contenuti disciplinari, per dar modo di spostare l’attenzione sulla scoperta, esplicitazione, generalizzazione e condivisione dei principi catturati durante tali attività di problem solving autentico. Tali esperienze di successo costituirebbero il giusto punto di partenza per passare ad attività di investigazione su contenuti scientifici disciplinari. Affrontando direttamente contenuti o problemi scientifici reali e/o generali e complessi, le indagini ad essi relative avrebbero poche speranze di scalfire la superficie dei problemi e caricherebbero la memoria di lavoro degli studenti con un elevato ‘rumore di fondo’, rendendo inevitabile il trascurare il lavoro sulle abilità di processo.
Web References
- w1 – Padilla MJ (1990) The Science Process Skills
- w2 – Laboratorio. Scaricare e/o eseguire
- w3 – Scienceduc
- w4 – Progetto ‘Pollen’
- w5 – Scaricare e/o eseguire i pacchetti software MOBL
- w6 – Scaricare le machine operatrici
Resources
- Atti della scuola europea estiva per formatori di formatori all’insegnamento delle scienze nella scuola primaria (tenuto ad Erice, 9-14 luglio 2005)
- Metzenberg S. Reading: The Most Important Science Process Skill
Review
Questo articolo affronta la questione dell’insegnamento delle abilità di processo scientifiche e lo raccomando agli insegnanti sia della scuola primaria, sia della secondaria. Esso pone in rilievo l’importanza di insegnare i principi dell’indagine scientifica dalla prima-seconda elementare in avanti e fornisce delle proposte operative.
Sølve Marie Tegner Stenmark, Norvegia





