Ο Γαλιλαίος και τα φεγγάρια του Δία: εξερευνώντας τον νυχτερινό ουρανό του 1610 Teach article
Μετάφραση από την Αιμιλία Ξανθοπούλου (Emily Xanthopoulos). Μάθετε πως εσείς και οι μαθητές σας μπορείτε να χρησιμοποιήσετε τα μαθηματικά για να μελετήσετε τα φεγγάρια…

Γαλιλέι (Justus Sutermans,
1636).
Εικόνα δημόσιας κυριότητας˙
Πηγή εικόνας: Wikimedia
Commons
Mια νύχτα του Ιανουαρίου το 1610, ο Γαλιλαίος Γαλιλέι παρατήρησε τον Δία μέσα από το τηλεσκόπιο του και είδε όπως νόμιζε τρεις αστέρες κοντά στον πλανήτη. Συνέχισε τις παρατηρήσεις του για περίπου δύο μήνες, και μέσα σε αυτόν τον χρόνο συνειδητοποίησε ότι επρόκειτο στην πραγματικότητα για τέσσερις ‘αστέρες’ που άλλαζαν την θέση τους γύρω από τον Δία. Ο Γαλιλαίος συμπέρανε ότι οι ‘αστέρες’ ήταν στην πραγματικότητα πλανήτες σε τροχιά γύρω από τον Δία – οι πλανήτες των Μεδίκων, όπως τους ονόμασε τότε, αλλά που είναι σήμερα γνωστοί ως τα φεγγάρια του Γαλιλαίου προς τιμήν αυτού που τους ανακάλυψε (εικόνα 1).
‘…Θα πρέπει να αποκαλύψω και να δημοσιεύσω στον κόσμο την περίσταση της ανακάλυψης και παρατήρησης τεσσάρων ΠΛΑΝΗΤΩΝ, που δεν έχουν παρατηρηθεί ποτέ από την αρχή του κόσμου μέχρι την εποχή μας…”
Γαλιλαίος Γαλιλέι στο Sidereus Nuncius (Αστρικός αγγελιοφόρος; 1610)

φεγγάρια του Γαλιλαίου Ιώ,
Ευρώπη, Γανυμήδης, και
Καλλιστώ (ο Δίας δεν είναι
στην ίδια κλίμακα όπως οι
δορυφόροι).
Η εικόνα είναι ευγενική
προσφορά του NASA Planetary
Photojourna
Αυτή η ανακάλυψη του Γαλιλαίου αποτελεί την βάση του προγράμματος που επινόησα για τους μαθητές μου στην φυσική στην τελευταία τάξη του λυκείου (17–18 χρονών) όταν διδάσκω το θέμα της απλής αρμονικής κίνησης. Το πρόγραμμα βασίζεται σε μια παρόμοια δραστηριότητα που ανέπτυξα πρωτύτερα, για την κίνηση του φεγγαριού του Γαλιλαίου Ιώ (Ribeiro, 2012). Το παρόν πρόγραμμα έχει σαν βάση την έρευνα, και έχει σαν στόχο να απασχολήσει τους μαθητές με μια πλούσια ποικιλία από επιστημονικές διαδικασίες – από την εξερεύνηση ιστορικών πλαισίων ως την λήψη και ανάλυση πειραματικών αποτελεσμάτων και την ανακοίνωση των συμπερασμάτων τους σε άλλους.
Ο σκοπός του προγράμματος είναι να αποδείξουν οι μαθητές ότι ο Γαλιλαίος είχε δίκιο όταν υποστήριξε ότι οι ‘αστέρες’ κοντά στον Δία ήταν στην πραγματικότητα οι δορυφόροι του πλανήτη. Για να το κάνουν αυτό, οι μαθητές συγκεντρώνουν δεδομένα για την κίνηση των φεγγαριών χρησιμοποιώντας μια προσομοίωση σε υπολογιστή, και δείχνοντας μετά ότι αυτή η κίνηση έχει τα χαρακτηριστικά της απλής αρμονικής κίνησης, με τον Δία στο κέντρο. Στο τέλος του προγράμματος, οι μαθητές δημιουργούν μια αναφορά (ένα έγγραφο η παρουσίαση) για να περιγράψουν τα ευρήματά τους και όλη την διαδικασία – και, ιδανικά, την μοιράζονται με μαθητές από άλλες χώρες ώστε να μάθουν να παρουσιάζουν μια επιστημονική εργασία σε διεθνές επίπεδο.
Η διάρκεια του προγράμματος ποικίλλει ανάλογα με το πως ο εκπαιδευτικός αποφασίζει να το προσεγγίσει. Πέρασα τέσσερις μήνες εργαζόμενη στο πρόγραμμα με τους μαθητές μου, αλλά αν εσείς δεν έχετε χρόνο για να πραγματοποιήσετε ολόκληρο το πρόγραμμα με τους μαθητές σας, μπορείτε να διαλέξετε επιμέρους δραστηριότητες από αυτό.
Απλή αρμονική κίνηση και ομαλή κυκλική κίνηση
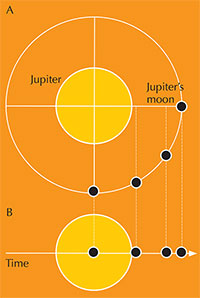
τα φεγγάρια του Γαλιλαίου
γύρω από τον Δία: Α) όπως
φαίνεται από πάνω από το
επίπεδο της τροχιάς και Β)
όπως φαίνεται από την Γη
(ορατό παράλληλα στο
επίπεδο της τροχιάς). Οι
μαύρες κουκίδες
αντιπροσωπεύουν τις θέσεις
των φεγγαριών του
Γαλιλαίου σε ίσα χρονικά
διαστήματα. Κάντε κλικ στην
εικόνα για μεγέθυνση.
Η εικόνα είναι ευγενική
προσφορά της Carla Isabel
Ribeiro
Η εικόνα είναι ευγενική προσφορά της Nicola Graf
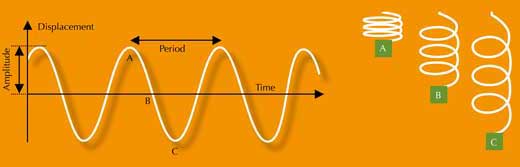
Απλή αρμονική κίνηση είναι ο όρος που χρησιμοποιείται για να περιγράψει τακτικές περιοδικές κινήσεις όπως της αιώρησης ενός εκκρεμούς η των ταλαντώσεων ενός αντικειμένου που συνδέεται σε ένα ελατήριο. Μια γραφική παράσταση αυτών των κινήσεων (της απόστασης από το κεντρικό σημείο ως προς τον χρόνο) δίνει την χαρακτηριστική μορφή ενός ημιτονοειδούς κύματος (εικόνα 2).
Η απλή αρμονική κίνηση μπορεί να ερμηνευτεί σαν μια προβολή πάνω σε έναν άξονα ενός αντικειμένου που κινείται με μια ομαλή κυκλική κίνηση. Για παράδειγμα, φανταστείτε ένα αντικείμενο που κινείται κυκλικά σε ένα οριζόντιο επίπεδο. Αν το δούμε από το πλάι στo ‘ύψος των ματιών’ (ισοδύναμο με την προβολή πάνω στον χ άξονα), βλέπουμε μια πέρα-δώθε κίνηση ακριβώς την ίδια με αυτήν ενός αντικειμένου συνδεδεμένο σε ελατήριο που βρίσκεται σε ταλάντωση. Μόνο όταν βλέπουμε την κίνηση από επάνω μπορούμε να δούμε την κίνηση ως κυκλική.
Αυτή η σχέση ανάμεσα στην απλή αρμονική κίνηση και την ομαλή κυκλική κίνηση μπορεί να εφαρμοστεί στα φεγγάρια του Γαλιλαίου όπως φαίνονται από την Γη: η κίνηση τους φαίνεται ως απλή αρμονική κίνηση, εξαιτίας της προβολής της ομαλής κυκλικής κίνησης τους γύρω από τον πλανήτη στην οπτική μας κατεύθυνση (εικόνα 3). (Οι τροχιές είναι ελαφρώς έκκεντρες, αλλά μόνο σε έναν μικρό βαθμό, και έτσι μπορεί να θεωρήσουμε ότι τα φεγγάρια έχουν κυκλική τροχιά και ότι κινούνται με σταθερή ταχύτητα.
Η κοσμολογία στην εποχή του Γαλιλαίου

μοντέλο του κόσμου του
16ου αιώνα, όπως
απεικονίζεται στην
Κοσμογραφία
(Cosmographia) (1568) του
Bartolomeu Velho. Κάντε κλικ
στην εικόνα για μεγέθυνση.
Εικόνα δημόσιας κυριότητας˙
Πηγή εικόνας: Wikimedia
Commons
Οι παρατηρήσεις των φεγγαριών του Δία από τον Γαλιλαίο έγιναν κατά την διάρκεια μια επιστημονικής μετάβασης, από το γεωκεντρικό (με την Γη στο επίκεντρο˙ εικόνα 4) μοντέλο του Αριστοτέλη και της Καθολικής Εκκλησίας στο ηλιοκεντρικό (με τον Ήλιο στο επίκεντρο) μοντέλο.
Ο Γαλιλαίος, φυσικά, θα έπαιρνε ρητά την θέση του ηλιοκεντρικού μοντέλου μερικά χρόνια μετά, σε μια άμεση πρόκληση προς το Καθολικό δόγμα. Παρόλα αυτά, οι παρατηρήσεις του με το τηλεσκόπιο, που δημοσιεύτηκαν στο βιβλίο του Sidereus Nuncius (Αστρικός αγγελιοφόρος) το 1610, είχαν ήδη προκαλέσει τριβή έρχοντας σε αντίθεση με τις διδασκαλίες του Αριστοτέλη. Στο μοντέλο του Αριστοτέλη, όλα στον κόσμο βρίσκονται σε τροχιά γύρω από την Γη – και έτσι η ιδέα των φεγγαριών να περιφέρονται γύρω από τον πλανήτη Δια ήταν σε αντίθεση με αυτό.
Το πρόγραμμα βήμα προς βήμα
Βήμα 1: Κοσμολογία του 17ou αιώνα
Ζητήστε από τους μαθητές σας να ερευνήσουν τις κοσμολογικές ιδέες που ίσχυαν στις αρχές του 17ου αιώνα στην Ευρώπη. Τι επίδραση μπορεί να είχαν στον Γαλιλαίο, στις έρευνες του και στα συμπεράσματα του; Οι μαθητές θα πρέπει να διαβάσουν επίσης αποσπάσματα από το Sidereus Nunciusw1, στο οποίο ο Γαλιλαίος περιγράφει τις παρατηρήσεις και τα συμπεράσματα του.
Βήμα 2: διαλέξτε το λογισμικό πλανητάριου
Θα χρειαστεί να κατεβάσετε από το διαδίκτυο το δωρεάν λογισμικό πλανητάριο πρόγραμμα Stellariumw2 η μια παρόμοια προσομοίωση. Μετά χωρίστε τους μαθητές σας σε τέσσερις ομάδες, και αναθέστε σε κάθε ομάδα ένα από τα τέσσερα φεγγάρια του Γαλιλαίου (Ιώ, Καλλιστώ, Γανυμήδη η Ευρώπη).
Βήμα 3: παρακολουθώντας τα φεγγάρια του Δία

Ζητήστε από τους μαθητές σας να χρησιμοποιήσουν το Stellarium για να ερευνήσουν την θέση του φεγγαριού τους με την πάροδο του χρόνου: σε έναν πίνακα, κάθε ομάδα θα πρέπει να καταγράφει την μετατόπιση (x) – την απόσταση του φεγγαριού τους από το κέντρο του Δία – σε μια διαδοχή χρόνων (t). Επίσης θα πρέπει να βρουν την μέγιστη μετατόπιση (A) του φεγγαριού από το κέντρο του πλανήτη.
Οι μετρήσεις θα πρέπει να ληφθούν κατά διαστήματα που διαφέρουν για τα τέσσερα φεγγάρια, ανάλογα με την απόσταση τους από τον πλανήτη, και επομένως, ανάλογα με την περίοδο της τροχιάς τους. Οι μαθητές θα πρέπει να χρησιμοποιήσουν την πρακτική της δοκιμής και του λάθους για να βρουν το πιο κατάλληλο διάστημα για το φεγγάρι τους. Ο σκοπός τους είναι να πάρουν τουλάχιστον 10 μετρήσεις, μια από τις οποίες θα πρέπει να είναι η A.

Για παράδειγμα, η Ιώ είναι το πιο κοντινό στον Δία φεγγάρι, που σημαίνει ότι περιφέρεται και πιο γρήγορα. Αν οι μαθητές πάρουν τις μετρήσεις τους ανά μια ώρα, τα δεδομένα δεν θα είναι αρκετά˙ διαστήματα 15 λεπτών θα είναι πιο κατάλληλα. Για ένα από τα πιο απομακρυσμένα φεγγάρια του Γαλιλαίου, διαστήματα 15 λεπτών θα είχαν σαν αποτέλεσμα πιο πολλά δεδομένα από αυτά που είναι αναγκαία, και επομένως ένα μεγαλύτερο διάστημα θα πρέπει να χρησιμοποιηθεί.
Για να βρουν το κέντρο του πλανήτη στο Stellarium, οι μαθητές σας μπορούν να χρησιμοποιήσουν τα κόκκινα σημάδια γύρω από τον Δία (εικόνα 5) για να σχεδιάσουν δύο γραμμές που διασταυρώνονται στο κέντρο του. Για να βρουν την απόσταση από αυτό το σημείο ως το φεγγάρι που μελετούν, μπορούν η να χρησιμοποιήσουν ένα πρόγραμμα εικόνας η να εκτυπώσουν τα αρχεία εικόνας που έχουν “συλλάβει” την εικόνα της επιφάνειας εργασίας του υπολογιστή και να μετρήσουν τις αποστάσεις με έναν χάρακα.

freeware programme
Stellarium of Jupiter and its
moons Europa (A) and Io (B).
Click on images to enlarge.
Images courtesy of Stellarium
Βήμα 4: ελέγξετε το συμπέρασμα του Γαλιλαίου
Το τέταρτο και το πιο πολύπλοκο βήμα είναι να δείξουν οι μαθητές ότι ο Γαλιλαίος είχε δίκιο όταν κατέληξε στο συμπέρασμα ότι η απλή αρμονική κίνηση που παρατήρησε προέρχεται από την ομαλή κυκλική κίνηση του φεγγαριού γύρω από τον πλανήτη του.
Για να βρουν την περίοδο της τροχιάς T των φεγγαριών του, οι μαθητές θα χρειαστούν την μαθηματική εξίσωση για την απλή αρμονική κίνηση:
x = A × sin(ω t + φ) (1)
όπου w είναι η γωνιακή συχνότητα και j είναι μια σταθερά (η σταθερά φάσης), μαζί με την εξίσωση που συνδέει το w και T:
ω = 2π / T
όπου x είναι η μετατόπιση, A το πλάτος της κίνησης η η μέγιστη μετατόπιση, t είναι ο χρόνος και j είναι η σταθερά (η σταθερά της φάσης).
Η εξίσωση (1) μπορεί να μετατραπεί στην γραμμική εξίσωση (2), έτσι:
x = A × sin(ω t + φ) (1)
→ x / A = sin(ω t + φ)
→ arcsin(x / A) = ω t + φ
Εφόσον ω = 2π / T
→ arcsin(x / A) = (2π / T)t + φ (2)
Αν οι μαθητές σας παρατηρήσουν ένα αντικείμενο να συμπεριφέρεται σύμφωνα με την εξίσωση (2) – που περιγράφει την απλή αρμονική κίνηση – τότε είναι λογικό να συμπεράνουν ότι περιφέρεται γύρω από τον πλανήτη όπως ένα φεγγάρι.
Επειδή η εξίσωση (2) είναι γραμμική, μπορούμε να δούμε ότι αν οι μαθητές σας χρησιμοποιήσουν τα δεδομένα τους από το βήμα 3 για να κάνουν μια γραφική παράσταση του arcsin(x / A) ως προς t, η κλίση θα είναι 2p / T, από την οποία μπορούν εύκολα να υπολογίσουν την περίοδο της τροχιάς T. Η σταθερά φάσης του φεγγαριού, j, είναι η τομή με τον άξονα y. Η εικόνα 6 δείχνει ένα παράδειγμα μιας γραφικής παράστασης που οι μαθητές σας μπορούν να σχεδιάσουν χρησιμοποιώντας δεδομένα από το φεγγάρι Ευρώπη.
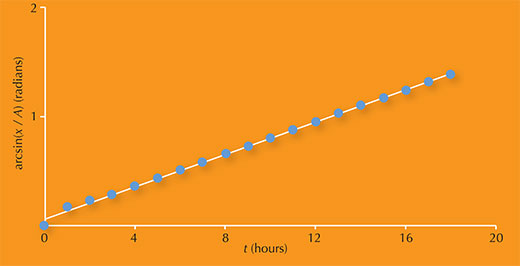
Η εικόνα είναι ευγενική προσφορά της Carla Isabel Ribeiro
Η παραπάνω γραφική παράσταση έχει κλίση ίση με 0.0741.
Εφόσον η κλίση είναι ίση με 2p / T, συνεπάγεται ότι:
2π / T = 0.0741
→ T = 2π / 0.0741
= 84.8 h
Οι πιο ικανοί στα μαθηματικά μαθητές μπορούν στην συνέχεια να προβούν σε μια ανάλυση παλινδρόμησης (regression analysis) των δεδομένων για τον έλεγχο της ‘καλής προσαρμογής’ (‘goodness of fit’) στην εξίσωση (2). Η τιμή που λαμβάνεται στην περίπτωση της Ευρώπης (R2 = 0.998) δείχνει ότι τα δεδομένα ακολουθούν στενά την εξίσωση, και επομένως επιβεβαιώνει ότι αυτό το αντικείμενο συμπεριφέρεται όπως ένα φεγγάρι σε τροχιά.
Η αποδεκτή τιμή για την Ευρώπη είναι περίπου 3.55 μέρες (85.2 ώρες), που είναι πολύ κοντά στην τιμή που υπολογίστηκε παραπάνω. Η διαφορά ανάμεσα στις δύο τιμές μπορεί να είναι μια καλή αρχή για μια συζήτηση για την ακρίβεια των πειραματικών αποτελεσμάτων. Τι μπορεί να πήγε λάθος; Ήταν κάποια από τα λάθη τυχαία η συστηματικά;
Σε αυτή την περίπτωση, το λάθος μπορεί να έχει τις ρίζες του στη μέτρηση του A, αφού οι θέσεις του φεγγαριού προσομοιώθηκαν κατά διαστήματα μιας ώρας, και η μέγιστη μετατόπιση μπορεί να είχε επιτευχθεί ανάμεσα στις δύο μετρήσεις. Μπορείτε να ρωτήσετε τους μαθητές σας να προτείνουν τρόπους για να ελαχιστοποιήσουν αυτό το λάθος.

στον Δόγη της Βενετίας πως
να χρησιμοποιεί το
τηλεσκόπιο του (HJ
Detouche, 1754). Κάντε κλικ
στην εικόνα για μεγέθυνση.
Εικόνα δημόσιας κυριότητας˙
Πηγή εικόνας:Wikimedia
Commons
Βήμα 5: παρουσιάζοντας τα αποτελέσματα
Το τελευταίο βήμα είναι να παρουσιάσει κάθε ομάδα μαθητών την δουλειά της, περιγράφοντας όλη την έρευνα και δείχνοντας τα αποτελέσματα της. Στις φυσικές επιστήμες, είναι σημαντική η επικοινωνία, και έτσι μπορείτε να βάλετε τους μαθητές σας να κάνουν τις παρουσιάσεις τους σε μαθητές μια άλλης τάξης, η να το κάνετε τμήμα μιας σχολικής έκθεσης η ημέρας γνωριμίας. Θα πρέπει να σκεφτούν πως να παρουσιάσουν καλύτερα την εργασία τους. Πως μπορούν να την κάνουν απλή ώστε να την καταλάβουν οι άλλοι; Τι εικόνες θα μπορούσαν να χρησιμοποιήσουν ώστε να τους βοηθήσει να εξηγήσουν τι έκαναν;
Πιο φιλόδοξα, θα μπορούσατε ακόμη να ξεκινήσετε μια συνεργασία με ένα σχολείο από ένα άλλο κράτος. Οι επιστήμονες μερικές φορές πρέπει να επικοινωνούν σε ξένες γλώσσες – συχνά, αλλά όχι πάντα, στα αγγλικά. Με βάση αυτό το πρόγραμμα, ελπίζω να δημιουργήσω μια παγκόσμια συνεργασία μέσω του eTwinning networkw3. Σε μικρότερη κλίμακα, θα χαρώ επίσης να ακούσω από άλλα σχολεία που θα ήθελαν να δουλέψουν μαζί στο πρόγραμμα.
References
- Ribeiro CI (2012) Io and its simple harmonic motion. Physics Education 47: 268-270. doi: 10.1088/0031-9120/47/3/F04
Web References
- w1 – Κατεβάστε μια πρόσφατη Αγγλική μετάφραση του Sidereus Nuncius (Starry Messenger στα αγγλικά), το περίφημο πρώιμο έργο του Γαλιλαίου που περιγράφει ανακαλύψεις που έγιναν με το τηλεσκόπιο. Οι σελίδες 17 και 18 περιέχουν τις παρατηρήσεις του από τα φεγγάρια του Δία για τις ημερομηνίες που παρουσιάζονται σε αυτό το πρόγραμμα.
-
Η αρχική έκδοση είναι επίσης διαθέσιμη στο διαδίκτυο.
-
- w2 – Το Stellarium, το πρόγραμμα προσομοίωσης πλανητών που χρησιμοποιήθηκε σε αυτό το πρόγραμμα, μπορεί να ληφθεί από το διαδίκτυο δωρεάν.
- w3 – Η eTwinning website προωθεί την συνεργασία σχολείων στην Ευρώπη μέσω της χρήσης των τεχνολογιών της πληροφορικής και επικοινωνίας (ICT). Διαθέσιμη σε 23 γλώσσες, έχει περίπου 50 000 μέλη και περισσότερα από 4000 εγγεγραμμένα προγράμματα μεταξύ δύο η περισσότερων σχολείων σε όλη την Ευρώπη.
Resources
- Η ιστοσελίδα Physclips παρέχει μια καθαρή εξήγηση της απλής αρμονικής κίνησης, με βίντεο και κινούμενα σχέδια.
- Η ιστοσελίδα της NASA για την Εξερεύνηση του Ηλιακού Συστήματος παρέχει πρόσφατες και ενημερωμένες πληροφορίες για τον Δία και τα φεγγάρια του, συμπεριλαμβανομένων και των διαστημικών αποστολών.
- Για ένα άρθρο που περιγράφει ένα παρόμοιο πρόγραμμα που εξερευνά τα φεγγάρια του Γαλιλαίου, χρησιμοποιώντας ένα τηλεσκόπιο εξοπλισμένο με μια διάταξη συζευγμένου φορτίου (CCD), δείτε το:
-
de Moraes IG, Pereira JAM (2009) Using simple harmonic motion to follow the Galilean moons – testing Kepler’s third law on a small system. Physics Education 44: 241. doi: 10.1088/0031-9120/44/3/002
-
Μπορείτε να κατεβάσετε δωρεάν το άρθρο από την ιστοσελίδα του Université de Picardie, Γαλλία.
-
- Το πρόγραμμα CLEA (Contemporary Laboratory Experiences in Astronomy) Σύγχρονες Εργαστηριακές Εμπειρίες στην Αστρονομία, που φιλοξενείται από το Gettysburg College, ΗΠΑ, προσφέρει εργαστηριακές ασκήσεις που απεικονίζουν σύγχρονες τεχνικές αστρονομίας. Κάθε άσκηση αποτελείται από ένα ειδικό πρόγραμμα ηλεκτρονικού υπολογιστή, ένα μαθητικό εγχειρίδιο, και έναν τεχνικό οδηγό για τον εκπαιδευτικό. Μερικές από τις ασκήσεις περιλαμβάνουν τα φεγγάρια του Δία.
Review
Αυτό το άρθρο προτείνει μια καινούργια μέθοδο διδασκαλίας της απλής αρμονικής κίνησης που βασίζεται στην έρευνα: οι μαθητές χρησιμοποιούν τις γνώσεις τους στα μαθηματικά, την φυσική και την τεχνολογία της πληροφορικής και επικοινωνίας για να παρουσιάσουν την κίνηση των φεγγαριών του Δία. Συλλέγουν δεδομένα από ένα λογισμικό, τα επεξεργάζονται, και μετά κάνουν γραφικές παραστάσεις, ειδικά των συναρτήσεων ημίτονου και συνημίτονου, για να υπολογίσουν τις περιόδους τροχιάς των φεγγαριών.
Η διεπιστημονική φύση του άρθρου χρησιμεύει για να κάνει τις φυσικές επιστήμες πιο ευχάριστες. Επιπλέον, η δραστηριότητα αναπτύσσει δεξιότητες όπως την παρουσίαση αποτελεσμάτων και την επικοινωνία. Συμμετέχοντας σε ένα διεθνές πρόγραμμα, οι μαθητές θα έχουν την ευκαιρία να μοιραστούν τα αποτελέσματα τους όχι μόνο με τα άλλα μέλη της τάξης τους αλλά και με μαθητές από διαφορετικά κράτη.
Corina Toma, Computer Science High School (Γυμνάσιο Πληροφορικής) “Tiberiu Popoviciu” Cluj Napoca, Ρουμανία





