Passa-t’ho pipa ! : ensenyant física a les muntanyes russes Teach article

Traduït per Jaume Pont Serra. Les muntanyes russes, els cavallets i altres atraccions dels parcs poden ser molt divertides - i fins i tot es poden utilitzar per fer una classe de ciències, com ens explica Giovanni Pezzi.

Un parc d’atraccions o una fira és un lloc ideal per fer experiments de física que mai no es podran dur a terme a l’aula. Hi ha projectes a tot el món que hi desenvolupen activitats d’aprenentatge (veure ‘Recursos’).

Un d’ells és “Mirabilandia, un’aula senza pareti” (“Mirabilandia, una aula sense parets”), un projecte italià que fou impulsat el 2002 pels professors de l’escola secundària de l’institut Torricelli de Faenza, en el seu parc d’atraccions local, Mirabilandia^w1. La iniciativa va tenir tant èxit que l’administració del parc va decidir posar-lo a disposició de totes les escoles i va organitzar viatges educatius per als estudiants de ciències.

Potser podríeu fer un acord semblant amb un parc d’atraccions local? Mentrestant, aquí teniu algunes de les activitats típiques per desenvolupar en qualsevol parc d’atraccions o fira. En alguns casos, primer hauríeu d’esbrinar les especificitats tècniques, ja sigui a través del parc o en línia, per exemple, a la base de dades Roller Coaster^w2. En una atracció, per fixar els instruments de mesura als cinturons de seguretat dels estudiants o a la pista de l’estructura de l’atracció, necessitareu el consentiment de les autoritats del parc. En el nostre cas, el director de l’escola va posar-se en contacte amb l’administració del parc i els va detallar el projecte que teníem pensat.

Les activitats són adequades per als nois de 15 a 19 anys, però es poden adaptar als més jovenets. Aquestes es refereixen al moviment rectilini i circular, la velocitat i l’ acceleració, la gravetat, la força centrípeta i la transformació de l’energia.

Els estudiants han d’estar familiaritzats amb els conceptes bàsics de cinemàtica i dinàmica, i disposar d’una introducció bàsica de les activitats abans de visitar el parc.

El temps previst de cada activitat és aproximadament d’ una hora, si bé pot augmentar a causa dels temps d’espera d’accés a l’atracció. Un equip pot realitzar els mesuraments a bord, mentre que altres treballen sobre el terreny. En general, no hi ha temps perquè cada grup repeteixi els mesuraments, però les dades dels diferents grups es poden comparar. Les avaluacions preliminars es poden fer al parc i continuar-les a classe.

A Mirabilandia, els estudiants reben un qüestionari per omplir. Una part es troba traduït a l’anglès i és a disposició de qui vulgui descarregar-lo^w3.

Muntanyes russes

Des de terra

Dibuixar un esbós en dues dimensions del perfil en alçada de la muntanya russa i discutir les transformacions de l’energia al llarg del camí, sobretot en el primer descens i els llaços verticals.

A la part superior de la muntanya russa, abans del primer descens, l’energia potencial gravitatòria és màxima, al llarg de la baixada, que sovint té una trajectòria parabòlica, és on els passatgers poden experimentar la ingravidesa durant uns segons (en el cas ideal sense fricció, el component vertical del moviment s’incrementa amb l’acceleració constant g a causa de la gravetat, com en una caiguda lliure), i aquesta es transforma en energia cinètica.

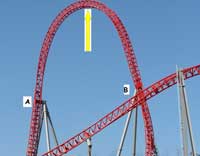
Utilitzar llaços verticals per discutir el paper de la gravetat en relació a la força centrípeta. Els llaços són en forma de gota, seguint el curs d’una clotoide corba, en què el radi de curvatura és inversament proporcional a la distància recorreguda sobre ella, cosa que redueix les acceleracions centrípetes en el llaç perquè sigui més còmode per als passatgers.

Només es pot saber la rapidesa en una muntanya russa fent un càlcul de la velocitat:

a) Calculeu la velocitat instantània dividint la longitud del tren de la muntanya russa pel temps necessari perquè tot el tren passi per un punt específic al llarg del recorregut.

b) Per obtenir la velocitat mitjana del tren al llarg d’un tram de la pista de la muntanya russa, trieu-ne un que sigui fàcil de veure i de forma senzilla. Compteu el nombre de travesses (barres espaiades regularment entre els rails) d’aquest tram i resteu-ne un per obtenir el nombre d’intervals. Calculeu el temps que triga el tren a recórrer aquest tram de via. Per calcular la distància recorreguda, es multiplica el nombre d’intervals per la longitud de l’interval (la distància entre dues travesses). Dividiu això pel temps utilitzat.

Compareu la velocitat instantània registrada al final del primer descens (la més ràpida) amb la velocitat calculada d’un cos en caiguda lliure: v = √ (2 g h), on v: velocitat, g : acceleració de la gravetat, h: alçada.

La velocitat ha de ser menor a causa de la fricció.

A la muntanya russa

Pareu atenció a les sensacions de lleugeresa o pesadesa (acceleració) que podeu experimentar al llarg d’alguns trams del recorregut. Dades més precises es poden obtenir amb acceleròmetres de molla o amb els instruments electrònics portàtils^w4. Les instruccions sobre com construir i /o obtenir-los i com avaluar els seus resultats estan disponibles a^w3.

Recentment, els telèfons intel·ligents amb un acceleròmetre de tres eixos s’han tornat més populars. La seva aplicació permet dibuixar gràfics d’acceleració en el temps o per mesurar els angles d’ inclinació. Comporten menys problemes de seguretat, ja que podeu portar-los a la butxaca.

Torres de caiguda

Torres de caiguda són pistes verticals de dalt a baix on els passatgers van asseguts en una góndola. N’hi ha d’un tipus on la góndola cau en caiguda lliure. En un altre tipus, la góndola és esmpesa cap avall o cap amunt amb una força superior a la de la gravetat.

Des de terra, es pot calcular la velocitat mitjana de descens de la góndola, només cal dividir l’altura de la torre pel temps de caiguda que mesureu amb un cronòmetre. Això pot ser comparat amb la velocitat instantània d’un cos en caiguda lliure. Per mesurar l’altura de la torre, utilitzeu un transportador i trigonometria bàsica o la geometria. Les instruccions detallades estan disponibles a^w3.

Durant el recorregut, es pot sentir l’acceleració en el cos i mesurar-la amb instruments electrònics portàtils de^w4.

En les torres on s’empeny la góndola, l’acceleració pot triplicar la gravetat.

Si preneu un got de plàstic ple d’aigua, es pot observar que en caiguda lliure l’aigua romandrà dins del got, però si la góndola és empesa cap avall, en lloc de caure, el nivell de l’aigua del got s’elevarà. Alternativament, es pot lligar una petita pilota de goma al canell (perforeu la pilota per lligar-hi una cadeneta) i poseu-la al palmell de la mà.

Nòries

Les activitats següents també són adequades per als estudiants més jovenets, amb edats entre els 11-14 anys. Han d’estar familiaritzats amb els conceptes de velocitat i de pressió atmosfèrica, i aprendran com funciona el moviment circular uniforme (temps, velocitat, freqüència) i com cal aplicar els seus coneixements sobre la pressió atmosfèrica. Ja sigui des de terra o des de la cistella, hauran de mesurar i anotar el temps després d’un quart de volta, mitja volta, un gir de tres quarts de volta i una volta completa de la roda.

Els estudiants han de descobrir que el temps necessari per a cada quart de volta és semblant. Per tant, el moviment de la roda és regular i a velocitat constant.

Calculeu la longitud del camí de la cistella (tenint en compte el radi de la roda), la seva velocitat mitjana, i, com a exercici de matemàtiques aplicades al món real, l’angle al centre de la roda entre les dues barres que es connecten dues cistelles veïnes a la centre (dividiu 360° pel nombre de góndoles).

Podeu determinar l’altura de la roda i de la torre de caiguda (veure a dalt) mitjançant l’ús de baròmetres electrònics per determinar el canvi en la pressió atmosfèrica durant el viatge.

Cada 0,1 kPa de canvi de pressió correspon a uns 8 m de desnivell. Una descripció més precisa de la relació entre la pressió i l’alçada està disponible en línia a^w5. Compareu els resultats i discutiu els avantatges i desavantatges de cada mètode (precisió, instruments, temps i esforç).

Cavallets

Els cavallets és el lloc perfecte per estudiar el pèndol de Foucault i l’efecte Coriolis. Els estudiants han d’estar familiaritzats amb el moviment d’un pèndol, les lleis del moviment, la gravetat, la força centrípeta, i la rotació. Els detalls de com realitzar aquests experiments estan disponibles a^w3.