Disease dynamics: understanding the spread of diseases Teach article

Get to grips with the spread of infectious diseases with these classroom activities highlighting real-life applications of school mathematics.

Schools are breeding grounds for infections: students are constantly interacting with each other, and often they have not yet built up immunities to disease. Understanding these interactions is vital for predicting how an infectious disease – such as influenza – will spread. For school students, it is important to think about their social interactions and to understand the types of analyses that can be used to determine disease dynamics.

These cross-curricular activities are for students aged 12–15, although some may be suitable for younger or older students too. The activities can be carried out by teams varying in size from small groups to the whole class. The resources do not require anything more than the slides that can be downloaded from the additional materials section^w1, paper and dice.

Activity 1: The standing disease

This short, whole-class activity simulates the outbreak of a disease, the symptom of which is standing up. The objective is to see how quickly the disease spreads exponentially across the classroom. With each step, the number of students that are infected doubles (see figure 1). This will help students to understand that it doesn’t take many steps for an outbreak to spread through a susceptible population.

Students will see that the rate at which a disease spreads is dependent on the number of individuals that are susceptible or infected. This is only a simple mathematical model for determining the spread of disease, however, since it assumes everyone is susceptible to infection and that exactly two individuals are infected by each person.

Procedure

1. Start with the whole class sitting down. Ask for one volunteer to be the first case.
2. This first volunteer should then stand up and ‘infect’ two classmates by pointing to them.
3. These two students then also stand up, having been infected.
4. Each of those two students then infects two more students in the classroom, and so on, until the whole class is standing up.
5. Ask the students how many steps it took to infect their class.

Discussion

• Ask your students to estimate how many steps it would take to infect their school, town, country or the world. It takes approximately 33 steps to infect the world with a population of 8.5 billion (as there are 2ⁿ new cases in generation n of the outbreak).
• What would happen if each person pointed to 3 or 4 people instead of 2?
• What can this tell us about how infectious diseases spread?
• What are the limitations of this simulation of an outbreak?

R₀ and networks

R₀ (otherwise known as the reproduction number) is a measure used in epidemiology to indicate the average number of people that an infected person infects during the course of the contagious period (assuming that no-one in the population is immune to the disease). If R₀ is greater than one, the disease will spread through the population. If R₀ is less than one, the cases of the disease will decrease and the outbreak will die out.

R₀ varies depending on how long the patient is contagious, the number of susceptible people in the population, and the method of transmission. Airborne diseases, such as measles, generally have a higher R₀ than those spread by bodily fluids, such as Ebola.

For epidemiologists, it is important to know not only the number of people that any one person may infect (R₀), but also how the outbreak may spread through a population. Thus, it is vital to understand the dynamics of the community or population. This is done by looking at how individuals interact with each other: who comes into contact with whom, and how often. Mathematical modellers can then build this information into their simulations to understand how an outbreak has spread through a population. This is vital for health researchers, as it helps them to trace individuals who may have become infected. It can also suggest which patterns of social behaviour may need to be changed if an outbreak does begin, such as social distancing or quarantine.

Although Ebola has the same low R₀ as flu, it quickly turned into a major outbreak in West Africa with a high mortality rate – something that would usually limit the spread of a disease because people die too quickly to infect a large group. What, then, were the major causes of the spread?

The epidemic was partly triggered by chance; the first person to be infected happened to be a traditional healer in Sierra Leone, whose funeral attracted a large crowd (Freiberger, 2015). The cultural tradition of washing the dead for burial led to increased transmission, and people who touched the infectious body took the disease with them as they travelled to other places. The outbreak was also in an area with weak health systems that were unable to enforce infection control.  

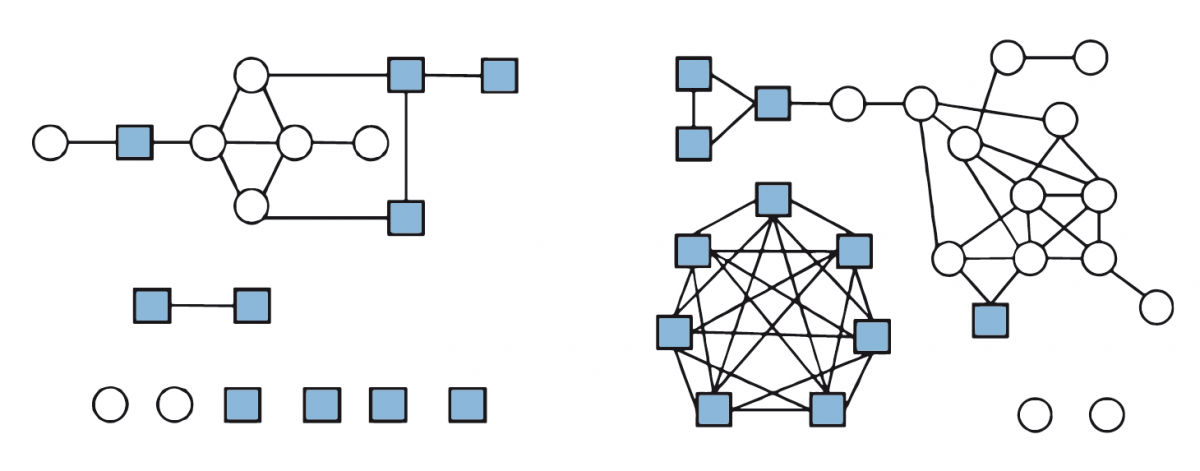
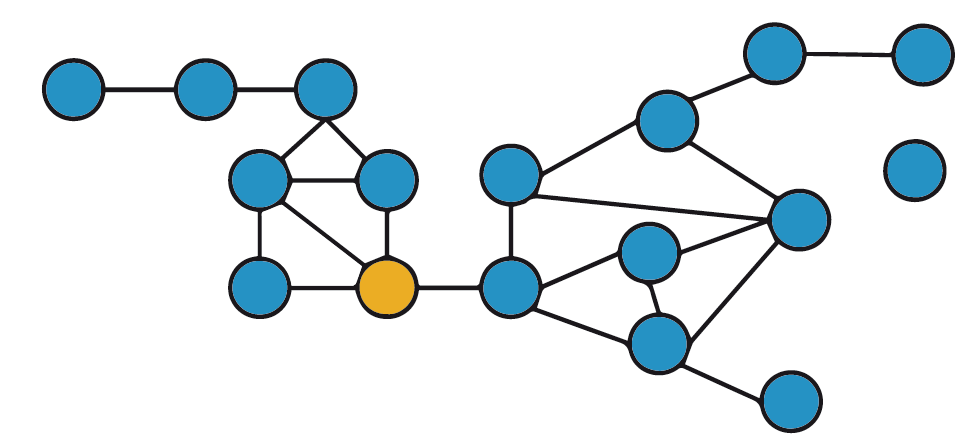
This example shows that the R₀ of a pathogen can vary in different outbreaks. The spread of flu, for example, is likely to be different in a group of 4- to 5-year-olds than in a group of 10- to 11-year-olds. Figure 2 shows the interactions between individuals in these two age groups on a particular school day. In the younger age group, there are fewer interactions between multiple individuals overall, compared to the older age group, in which two larger cliques of each sex are evident. The individual nodes with no interactions indicate that a student was absent on that day.

Activity 2: R₀ ranking

Procedure

1. In small groups, ask your students to list five infectious diseases (rabies, flu, Ebola, chickenpox and measles) in order of which they think has the highest and lowest reproduction number. Then reveal each R₀ (0, 1–2, 1–2, 10, 16–18, respectively) – were they what the students expected?

Discussion

• Is there a connection between the severity of symptoms and R₀?
• What can you say about the diseases with high R₀ (e.g. measles and chickenpox) – why are they so high?
• Why is the R₀ for rabies 0? There is no known human-to-human transmission.
• Why is Ebola cause for concern, when it has a low R₀ value?
• Why can the R₀ of the same pathogen vary in different outbreaks?

Activity 3: Comparing networks

Procedure

1. Show the whole class the diagrams^w1 of two different social networks: one with 4- to 5-year-olds, and one with 10- to 11-year-olds (see figure 2). Ask them what they think the difference is.
2. Discuss why these networking patterns may differ over time.

Discussion

• How/why does the social network change between 4- to 5-year-olds and 10- to 11-year-olds?
• Would you expect this network to change again for 16-year-olds? What about for adults?

Activity 4: Disease spread through a network

Procedure

1. Separate the class into pairs or small groups. Give each group printouts of a social network^w1 (figure 3) along with a dice.
2. Everyone starts off susceptible; pick one point of the network on the printout to be the first infected person.
3. Go around the infected person’s contacts in turn. For each one, roll the dice; if they roll a 1 or a 2, that person also becomes infected. If they roll any other number, they are immune.
4. Repeat for the new infected cases – and so on, until you have rolled the dice for every infected person’s contacts.
5. Count how many cases in the group are infected, and how many steps it took in total to infect them all.
6. Repeat the exercise several times, with different starting points. Note the number of cases each time.
7. These data can then be used for further analysis, e.g. mean, median, mode and distribution. Get students to plot graphs (e.g. figure 4) and analyse their results amongst their small group – or as a whole class. 

Discussion

• Why are we only infecting those nodes when a 1 or 2 is rolled?
• What would happen if we allowed 1, 2, 3 or 4 to infect someone?
• What happens if you start in different places around the network?
• Why does the outbreak change in size each time it is simulated?

Extension activity: targeted vaccination

Students can do consider these questions individually and then feed back to the whole class:

• Who would you vaccinate in the network?
• If you only had 2 or 3 doses of vaccine for the network, who would you choose to vaccinate and why?
• Would you protect people with the greatest number of links, or concentrate on breaking the network in certain places?

Acknowledgement

The teaching activities in this article are adapted from the NRICH^w2 Disease Dynamics series. Additional activities are available in this collection, which aims to show how maths can be used to understand epidemics, social interactions and vaccination.